1. Streaming from vibrating objects
It must have been a wonderful surprise, the discovery of the streaming wind by Faraday (Reference Faraday1831), when he observed the streams of air above vibrating plates showing the famous Chladni patterns. These steady vortices play a key role in moving very light particles on top of the plate, gathering particles in specific nodes, different from those followed by the heavy particles bouncing and reaching vibration nodes. The same streaming phenomenon occurs within a Kundt tube, gathering lycopodia particles at specific nodes.
We should first stress that it is not that usual that vibrations induce flow. The reverse phenomenon is more common: steady flows induce vibrations by the apparition of a self-sustained vibration of a boundary. An example is the pleasant singing of vocal cords vibrating under the air exhaled out of our lungs, or the harsh noise from the turbulent wake behind a high-speed vehicle.
Why do tiny vibrations induce a steady flow in a fluid? The vibration may come from the solid or, equivalently, from the flow around a fixed object. According to the well-know Stokes second problem, the tangential vibration of the solid boundary shears the fluid alternately back and forth, and this shear ‘diffuses’ into the fluid because of inner viscous forces. It sets an oscillatory boundary layer in the fluid near the solid body whose thickness scales as 
$\delta \sim (\nu /\omega )^{1/2}$, with $\nu$ the kinematic viscosity and $\omega$ the pulsation frequency. A non-dimensional number can be defined: the ratio of the typical size $L$ of the object to this boundary layer thickness $\delta$, known as the Womersley number and defined as $M=L/ (\nu /\omega )^{1/2}$.
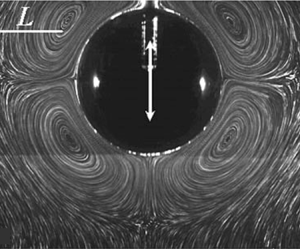
Within this layer, inertia plays a role, especially if there are velocity gradients involved. The nonlinear term of the Navier–Stokes equations provides a steady forcing which is quadratic in the oscillation amplitude. As a result, the sinusoidal vibration is rectified by this nonlinearity into a steady flow pattern. The steady flow velocity is also quadratic in the oscillation amplitude, while the geometry of the pattern depends only on the oscillation frequency. A beautiful visualisation of a steady flow around a rigid sphere is given in figure 1 taken from Kotas, Yoda & Rogers (Reference Kotas, Yoda and Rogers2006).
Figure 1. Streaming flow around a vibrating rigid acrylic sphere. The fluid is a solution of 90 % glycerin by weight, seeded with particles. The ratio of the object size $L$ to the oscillatory boundary layer thickness is such that $M=6$, with $L=$ 1.4 cm. Reproduced with permission from Kotas et al. (Reference Kotas, Yoda and Rogers2006).
Note that the streaming flow may give rise to very strong velocities: it is then called Stuart streaming if the Reynolds number associated with the streaming velocity and object size is large, while it is called Rayleigh–Nyborg–Westervelt streaming if this Reynolds number is small (Lighthill Reference Lighthill1978).
2. Introducing a touch of softness
The derivation of the streaming flow field is a complex calculation. It has been solved in several cases: around a rigid cylinder or sphere whose centre of mass oscillates. The geometry of the object is important, for instance, it was recently shown that in channels, sharp edges intensify the streaming at the tip of the edge (Zhang et al. Reference Zhang, Guo, Royon and Brunet2020). Conversely, some geometries can nearly suppress acoustic streaming, as shown by Bach & Bruus (Reference Bach and Bruus2020). In other derivations, a more complex vibration of the object was imposed to compute the flow, such as around solids exhibiting arbitrary shape modes (Spelman & Lauga Reference Spelman and Lauga2017), or around bubbles vibrating in both translation and radius (Longuet-Higgins Reference Longuet-Higgins1998), giving rise to specific vortices, or around liquid droplets (Rednikov Reference Rednikov2006).
Most prior streaming derivations considered rigid body motions or fluid objects. The full elasticity of the object was considered recently by Doinikov, Fankhauser & Dual (Reference Doinikov, Fankhauser and Dual2021). Cui, Bhosale & Gazzola (Reference Cui, Bhosale and Gazzola2024) fill a gap in the literature by considering an elastic (or visco-elastic) solid in a particularly useful geometry. The geometry of the problem is very simple: it consists of an elastic sphere containing a rigid spherical core. The vibration is imposed by a back and forth motion of the liquid around the object, the solid core being fixed. By a change of reference, this is equivalent to assuming that the solid core is driven by a given oscillation in translation. The flexibility of the sphere surface is now involved in the streaming.
3. An elaborate analytical solution
The three-dimensional (3-D) derivation is performed in spherical coordinates around the sphere. It follows the same steps as the two-dimensional calculation around a soft cylinder made by the same team (Bhosale, Parthasarathy & Gazzola Reference Bhosale, Parthasarathy and Gazzola2022).
The analytical derivation is an elaborate and lengthy piece of work. It is a noteworthy solution of the Navier–Stokes equations for small vibration amplitudes, including an elastic solid. In practice, it consists of a perturbation series of the Navier–Stokes equation, using an asymptotic expansion in powers of the vibration amplitude. It can be decomposed in the following steps.
(i) The first order of the perturbation in powers of the amplitude gives the back and forth (acoustic) vibration of the fluid. The originality is that here, the vibration within the solid displacement is also derived.
(ii) The second order gives the steady streaming, forced by nonlinear terms. One then obtains a steady flow which is an Eulerian flow field.
(iii) The Lagrangian flow field is computed to obtain the trajectories of tracer particles in this flow by adding the Stokes drift (Lighthill Reference Lighthill1978). This effect originates from the fact that particles embedded in the field oscillate in position and therefore experience different flow velocities, which result in a drift in addition to the Eulerian flow.
The final result is an analytical solution of all the vibration fields in the solid and in the fluid, and of course of the steady streaming flow. It correctly predicts typical streaming flows with an inner layer and an outer layer (see again figure 1). A simple observation of the flow field which confirm this theory is the measurement of thickness of the inner layer. The authors observe that with a softer elastic solid, the same inner layer thickness can be obtained with a lower frequency of vibration. The elastic vibration seems to decrease the extent of the inner layer, provided the elastic shear modulus is small in front of the fluid inertial forces.
4. Implications for outcomes in biology, microfluidics and robotics
These results will be of high interest in three fields of research. First, these results will be important for biological fluids where it is common to observe a pulsation of the flow, or for oscillating boundaries which generate steady streaming patterns in soft environments. Examples of such streaming situations are flows within the alveoli of the lungs due to breathing (Kumar et al. Reference Kumar, Tawhai, Hoffman and Lin2011), rectified flows due to intestinal villi (Puthumana Melepattu & de Loubens Reference Puthumana Melepattu and de Loubens2022) or flow induced by the vibration of otolith stones in fish ears (Kotas et al. Reference Kotas, Yoda and Rogers2006). In medicine, acoustic streaming flows enhance the delivery of drugs or accelerate the healing of injuries. The derivation by the authors might help to quantify the exact direction of circulation of the fluid around these objects, by predicting the extent of the inner boundary layer as well as the streaming velocities.
Second, microfluidic flows are an important possible outcome, since microfluidic channels are usually made of soft elastomeric materials, or because they contain soft or biological objects circulating. Many microfluidic applications rely on sound oscillations to set the fluid in motion, a convenient way to move fluid at small scales without external pumps (Muller et al. Reference Muller, Barnkob, Jensen and Bruus2012) to mix or to propel fluids. There we envision that the streaming predictions will be useful for the development of hybrid systems consisting of solid parts covered by soft elastomeric or biological layers, while set into vibration.
Finally, the fields of robotics and micro-swimmers could also benefit from this study. Swimming can be achieved from steady streaming (Dombrowski et al. Reference Dombrowski, Jones, Katsikis, Bhalla, Griffith and Klotsa2019), and considering a body with an elastic part is a natural extension. 3-D printing technologies allow the manufacturing of soft micro-propellers or micro-swimmers down to micrometric scales (Kaynak, Dirix & Sakar Reference Kaynak, Dirix and Sakar2020). The design of these objects will benefit from the streaming predictions, for the choice of the elasticity or the thickness of those materials, to enhance their velocities.
To conclude, we envision that this study will have ramifications at the fundamental level as well. The analytical derivations by Cui et al. (Reference Cui, Bhosale and Gazzola2024) still need to be compared with experiments: this work calls for new fluid mechanics experiments on vibrating soft spheres.
$L$ to the oscillatory boundary layer thickness is such that 
$M=6$, with 
$L=$ 1.4 cm. Reproduced with permission from Kotas et al. (2006).
You have
Access
1. Streaming from vibrating objects
It must have been a wonderful surprise, the discovery of the streaming wind by Faraday (Reference Faraday1831), when he observed the streams of air above vibrating plates showing the famous Chladni patterns. These steady vortices play a key role in moving very light particles on top of the plate, gathering particles in specific nodes, different from those followed by the heavy particles bouncing and reaching vibration nodes. The same streaming phenomenon occurs within a Kundt tube, gathering lycopodia particles at specific nodes.
We should first stress that it is not that usual that vibrations induce flow. The reverse phenomenon is more common: steady flows induce vibrations by the apparition of a self-sustained vibration of a boundary. An example is the pleasant singing of vocal cords vibrating under the air exhaled out of our lungs, or the harsh noise from the turbulent wake behind a high-speed vehicle.
Why do tiny vibrations induce a steady flow in a fluid? The vibration may come from the solid or, equivalently, from the flow around a fixed object. According to the well-know Stokes second problem, the tangential vibration of the solid boundary shears the fluid alternately back and forth, and this shear ‘diffuses’ into the fluid because of inner viscous forces. It sets an oscillatory boundary layer in the fluid near the solid body whose thickness scales as
$\delta \sim (\nu /\omega )^{1/2}$, with 
$\nu$ the kinematic viscosity and 
$\omega$ the pulsation frequency. A non-dimensional number can be defined: the ratio of the typical size 
$L$ of the object to this boundary layer thickness 
$\delta$, known as the Womersley number and defined as 
$M=L/ (\nu /\omega )^{1/2}$.
Within this layer, inertia plays a role, especially if there are velocity gradients involved. The nonlinear term of the Navier–Stokes equations provides a steady forcing which is quadratic in the oscillation amplitude. As a result, the sinusoidal vibration is rectified by this nonlinearity into a steady flow pattern. The steady flow velocity is also quadratic in the oscillation amplitude, while the geometry of the pattern depends only on the oscillation frequency. A beautiful visualisation of a steady flow around a rigid sphere is given in figure 1 taken from Kotas, Yoda & Rogers (Reference Kotas, Yoda and Rogers2006).
Figure 1. Streaming flow around a vibrating rigid acrylic sphere. The fluid is a solution of 90 % glycerin by weight, seeded with particles. The ratio of the object size
$L$ to the oscillatory boundary layer thickness is such that 
$M=6$, with 
$L=$ 1.4 cm. Reproduced with permission from Kotas et al. (Reference Kotas, Yoda and Rogers2006).
Note that the streaming flow may give rise to very strong velocities: it is then called Stuart streaming if the Reynolds number associated with the streaming velocity and object size is large, while it is called Rayleigh–Nyborg–Westervelt streaming if this Reynolds number is small (Lighthill Reference Lighthill1978).
2. Introducing a touch of softness
The derivation of the streaming flow field is a complex calculation. It has been solved in several cases: around a rigid cylinder or sphere whose centre of mass oscillates. The geometry of the object is important, for instance, it was recently shown that in channels, sharp edges intensify the streaming at the tip of the edge (Zhang et al. Reference Zhang, Guo, Royon and Brunet2020). Conversely, some geometries can nearly suppress acoustic streaming, as shown by Bach & Bruus (Reference Bach and Bruus2020). In other derivations, a more complex vibration of the object was imposed to compute the flow, such as around solids exhibiting arbitrary shape modes (Spelman & Lauga Reference Spelman and Lauga2017), or around bubbles vibrating in both translation and radius (Longuet-Higgins Reference Longuet-Higgins1998), giving rise to specific vortices, or around liquid droplets (Rednikov Reference Rednikov2006).
Most prior streaming derivations considered rigid body motions or fluid objects. The full elasticity of the object was considered recently by Doinikov, Fankhauser & Dual (Reference Doinikov, Fankhauser and Dual2021). Cui, Bhosale & Gazzola (Reference Cui, Bhosale and Gazzola2024) fill a gap in the literature by considering an elastic (or visco-elastic) solid in a particularly useful geometry. The geometry of the problem is very simple: it consists of an elastic sphere containing a rigid spherical core. The vibration is imposed by a back and forth motion of the liquid around the object, the solid core being fixed. By a change of reference, this is equivalent to assuming that the solid core is driven by a given oscillation in translation. The flexibility of the sphere surface is now involved in the streaming.
3. An elaborate analytical solution
The three-dimensional (3-D) derivation is performed in spherical coordinates around the sphere. It follows the same steps as the two-dimensional calculation around a soft cylinder made by the same team (Bhosale, Parthasarathy & Gazzola Reference Bhosale, Parthasarathy and Gazzola2022).
The analytical derivation is an elaborate and lengthy piece of work. It is a noteworthy solution of the Navier–Stokes equations for small vibration amplitudes, including an elastic solid. In practice, it consists of a perturbation series of the Navier–Stokes equation, using an asymptotic expansion in powers of the vibration amplitude. It can be decomposed in the following steps.
(i) The first order of the perturbation in powers of the amplitude gives the back and forth (acoustic) vibration of the fluid. The originality is that here, the vibration within the solid displacement is also derived.
(ii) The second order gives the steady streaming, forced by nonlinear terms. One then obtains a steady flow which is an Eulerian flow field.
(iii) The Lagrangian flow field is computed to obtain the trajectories of tracer particles in this flow by adding the Stokes drift (Lighthill Reference Lighthill1978). This effect originates from the fact that particles embedded in the field oscillate in position and therefore experience different flow velocities, which result in a drift in addition to the Eulerian flow.
The final result is an analytical solution of all the vibration fields in the solid and in the fluid, and of course of the steady streaming flow. It correctly predicts typical streaming flows with an inner layer and an outer layer (see again figure 1). A simple observation of the flow field which confirm this theory is the measurement of thickness of the inner layer. The authors observe that with a softer elastic solid, the same inner layer thickness can be obtained with a lower frequency of vibration. The elastic vibration seems to decrease the extent of the inner layer, provided the elastic shear modulus is small in front of the fluid inertial forces.
4. Implications for outcomes in biology, microfluidics and robotics
These results will be of high interest in three fields of research. First, these results will be important for biological fluids where it is common to observe a pulsation of the flow, or for oscillating boundaries which generate steady streaming patterns in soft environments. Examples of such streaming situations are flows within the alveoli of the lungs due to breathing (Kumar et al. Reference Kumar, Tawhai, Hoffman and Lin2011), rectified flows due to intestinal villi (Puthumana Melepattu & de Loubens Reference Puthumana Melepattu and de Loubens2022) or flow induced by the vibration of otolith stones in fish ears (Kotas et al. Reference Kotas, Yoda and Rogers2006). In medicine, acoustic streaming flows enhance the delivery of drugs or accelerate the healing of injuries. The derivation by the authors might help to quantify the exact direction of circulation of the fluid around these objects, by predicting the extent of the inner boundary layer as well as the streaming velocities.
Second, microfluidic flows are an important possible outcome, since microfluidic channels are usually made of soft elastomeric materials, or because they contain soft or biological objects circulating. Many microfluidic applications rely on sound oscillations to set the fluid in motion, a convenient way to move fluid at small scales without external pumps (Muller et al. Reference Muller, Barnkob, Jensen and Bruus2012) to mix or to propel fluids. There we envision that the streaming predictions will be useful for the development of hybrid systems consisting of solid parts covered by soft elastomeric or biological layers, while set into vibration.
Finally, the fields of robotics and micro-swimmers could also benefit from this study. Swimming can be achieved from steady streaming (Dombrowski et al. Reference Dombrowski, Jones, Katsikis, Bhalla, Griffith and Klotsa2019), and considering a body with an elastic part is a natural extension. 3-D printing technologies allow the manufacturing of soft micro-propellers or micro-swimmers down to micrometric scales (Kaynak, Dirix & Sakar Reference Kaynak, Dirix and Sakar2020). The design of these objects will benefit from the streaming predictions, for the choice of the elasticity or the thickness of those materials, to enhance their velocities.
To conclude, we envision that this study will have ramifications at the fundamental level as well. The analytical derivations by Cui et al. (Reference Cui, Bhosale and Gazzola2024) still need to be compared with experiments: this work calls for new fluid mechanics experiments on vibrating soft spheres.
Acknowledgements
The manuscript benefited from the reading of A.A. Doinikov and J. Neufeld. They are warmly acknowledged.
Declaration of interests
The author reports no conflict of interest.