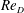 $Re_{D}$ from
$Re_{D}$ from 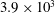 $3.9\times 10^{3}$ to
$3.9\times 10^{3}$ to 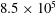 $8.5\times 10^{5}$: a skin-friction perspective
$8.5\times 10^{5}$: a skin-friction perspectivePublished online by Cambridge University Press: 05 May 2017
We present wall-resolved large-eddy simulations (LES) of flow over a smooth-wall circular cylinder up to 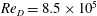 $Re_{D}=8.5\times 10^{5}$, where
$Re_{D}=8.5\times 10^{5}$, where  $Re_{D}$ is Reynolds number based on the cylinder diameter
$Re_{D}$ is Reynolds number based on the cylinder diameter 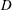 $D$ and the free-stream speed
$D$ and the free-stream speed 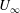 $U_{\infty }$. The stretched-vortex subgrid-scale (SGS) model is used in the entire simulation domain. For the sub-critical regime, six cases are implemented with
$U_{\infty }$. The stretched-vortex subgrid-scale (SGS) model is used in the entire simulation domain. For the sub-critical regime, six cases are implemented with 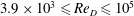 $3.9\times 10^{3}\leqslant Re_{D}\leqslant 10^{5}$. Results are compared with experimental data for both the wall-pressure-coefficient distribution on the cylinder surface, which dominates the drag coefficient, and the skin-friction coefficient, which clearly correlates with the separation behaviour. In the super-critical regime, LES for three values of
$3.9\times 10^{3}\leqslant Re_{D}\leqslant 10^{5}$. Results are compared with experimental data for both the wall-pressure-coefficient distribution on the cylinder surface, which dominates the drag coefficient, and the skin-friction coefficient, which clearly correlates with the separation behaviour. In the super-critical regime, LES for three values of  $Re_{D}$ are carried out at different resolutions. The drag-crisis phenomenon is well captured. For lower resolution, numerical discretization fluctuations are sufficient to stimulate transition, while for higher resolution, an applied boundary-layer perturbation is found to be necessary to stimulate transition. Large-eddy simulation results at
$Re_{D}$ are carried out at different resolutions. The drag-crisis phenomenon is well captured. For lower resolution, numerical discretization fluctuations are sufficient to stimulate transition, while for higher resolution, an applied boundary-layer perturbation is found to be necessary to stimulate transition. Large-eddy simulation results at 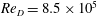 $Re_{D}=8.5\times 10^{5}$, with a mesh of
$Re_{D}=8.5\times 10^{5}$, with a mesh of 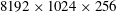 $8192\times 1024\times 256$, agree well with the classic experimental measurements of Achenbach (J. Fluid Mech., vol. 34, 1968, pp. 625–639) especially for the skin-friction coefficient, where a spike is produced by the laminar–turbulent transition on the top of a prior separation bubble. We document the properties of the attached-flow boundary layer on the cylinder surface as these vary with
$8192\times 1024\times 256$, agree well with the classic experimental measurements of Achenbach (J. Fluid Mech., vol. 34, 1968, pp. 625–639) especially for the skin-friction coefficient, where a spike is produced by the laminar–turbulent transition on the top of a prior separation bubble. We document the properties of the attached-flow boundary layer on the cylinder surface as these vary with 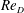 $Re_{D}$. Within the separated portion of the flow, mean-flow separation–reattachment bubbles are observed at some values of
$Re_{D}$. Within the separated portion of the flow, mean-flow separation–reattachment bubbles are observed at some values of 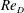 $Re_{D}$, with separation characteristics that are consistent with experimental observations. Time sequences of instantaneous surface portraits of vector skin-friction trajectory fields indicate that the unsteady counterpart of a mean-flow separation–reattachment bubble corresponds to the formation of local flow-reattachment cells, visible as coherent bundles of diverging surface streamlines.
$Re_{D}$, with separation characteristics that are consistent with experimental observations. Time sequences of instantaneous surface portraits of vector skin-friction trajectory fields indicate that the unsteady counterpart of a mean-flow separation–reattachment bubble corresponds to the formation of local flow-reattachment cells, visible as coherent bundles of diverging surface streamlines.