Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T13:25:55.861Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation of flow over a grooved cylinder up to transcritical Reynolds numbers

Published online by Cambridge University Press:  27 November 2017

W. Cheng Open the ORCID record for W. Cheng [Opens in a new window] ,
D. I. Pullin  and
R. Samtaney
W. Cheng*
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, 23955-6900, Saudi Arabia Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
R. Samtaney
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, 23955-6900, Saudi Arabia
*
†Email address for correspondence: chengw@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We report wall-resolved large-eddy simulation (LES) of flow over a grooved cylinder up to the transcritical regime. The stretched-vortex subgrid-scale model is embedded in a general fourth-order finite-difference code discretization on a curvilinear mesh. In the present study 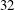$32$ grooves are equally distributed around the circumference of the cylinder, each of sinusoidal shape with height $\unicode[STIX]{x1D716}$, invariant in the spanwise direction. Based on the two parameters, 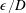$\unicode[STIX]{x1D716}/D$ and the Reynolds number 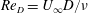$Re_{D}=U_{\infty }D/\unicode[STIX]{x1D708}$ where 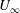$U_{\infty }$ is the free-stream velocity, 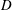$D$ the diameter of the cylinder and $\unicode[STIX]{x1D708}$ the kinematic viscosity, two main sets of simulations are described. The first set varies 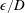$\unicode[STIX]{x1D716}/D$ from 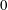$0$ to 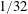$1/32$ while fixing 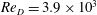$Re_{D}=3.9\times 10^{3}$. We study the flow deviation from the smooth-cylinder case, with emphasis on several important statistics such as the length of the mean-flow recirculation bubble 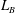$L_{B}$, the pressure coefficient 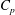$C_{p}$, the skin-friction coefficient 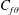$C_{f\unicode[STIX]{x1D703}}$ and the non-dimensional pressure gradient parameter 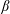$\unicode[STIX]{x1D6FD}$. It is found that, with increasing 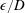$\unicode[STIX]{x1D716}/D$ at fixed 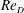$Re_{D}$, some properties of the mean flow behave somewhat similarly to changes in the smooth-cylinder flow when 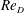$Re_{D}$ is increased. This includes shrinking 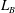$L_{B}$ and nearly constant minimum pressure coefficient. In contrast, while the non-dimensional pressure gradient parameter 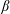$\unicode[STIX]{x1D6FD}$ remains nearly constant for the front part of the smooth cylinder flow, 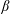$\unicode[STIX]{x1D6FD}$ shows an oscillatory variation for the grooved-cylinder case. The second main set of LES varies 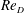$Re_{D}$ from 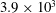$3.9\times 10^{3}$ to 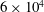$6\times 10^{4}$ with fixed 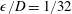$\unicode[STIX]{x1D716}/D=1/32$. It is found that this 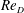$Re_{D}$ range spans the subcritical and supercritical regimes and reaches the beginning of the transcritical flow regime. Mean-flow properties are diagnosed and compared with available experimental data including 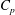$C_{p}$ and the drag coefficient 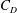$C_{D}$. The timewise variation of the lift and drag coefficients are also studied to elucidate the transition among three regimes. Instantaneous images of the surface, skin-friction vector field and also of the three-dimensional Q-criterion field are utilized to further understand the dynamics of the near-surface flow structures and vortex shedding. Comparison of the grooved-cylinder flow with the equivalent flow over a smooth-wall cylinder shows structural similarities but significant differences. Both flows exhibit a clear common signature, which is the formation of mean-flow secondary separation bubbles that transform to other local flow features upstream of the main separation region (prior separation bubbles) as 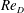$Re_{D}$ is increased through the respective drag crises. Based on these similarities it is hypothesized that the drag crises known to occur for flow past a cylinder with different surface topographies is the result of a change in the global flow state generated by an interaction of primary flow separation with secondary flow recirculating motions that manifest as a mean-flow secondary bubble. For the smooth-wall flow this is accompanied by local boundary-layer flow transition to turbulence and a strong drag crisis, while for the grooved-cylinder case the flow remains laminar but unsteady through its drag crisis and into the early transcritical flow range.

JFM classification

Boundary Layers: Boundary layer separation Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 327 - 362
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1968 Distribuion of local pressure and skin friction around a circular cylinder in cross-flow up to Re = 5 × 106 . J. Fluid Mech. 34, 625–639.Google Scholar
Achenbach, E. 1971 Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 46, 321–335.Google Scholar
Achenbach, E. & Heinecke, E. 1981 On vortex shedding from smooth and rough cylinders in the range of Reynolds numbers 6 × 103 to 5 × 106 . J. Fluid Mech. 109, 239–251.Google Scholar
Beaudan, P. & Moin, P.1994 Numerical experiments on the flow past a circular cylinder at sub-critical Reynolds number. Tech. Rep. TF-62. Stanford University.Google Scholar
Breuer, M. 2000 A challenging test case for large eddy simulation: high Reynolds number circular cylinder flow. Intl J. Heat Fluid Flow 21, 648–654.Google Scholar
Cardell, G. S.1993 Flow past a circular cylinder with a permeable splitter plate. PhD thesis, California Institute of Technology.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Cheng, W., Pullin, D. I. & Samtaney, R. 2015 Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer. J. Fluid Mech. 785, 78–108.CrossRefGoogle Scholar
Cheng, W., Pullin, D. I., Samtaney, R., Zhang, W. & Gao, W. 2017 Large-eddy simulation of flow over a cylinder with Re D from 3. 9 × 103 to 8. 5 × 105 : a skin-friction perspective. J. Fluid Mech. 820, 121–158.Google Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24, 011702.Google Scholar
Chung, D. & Pullin, D. I. 2009 Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 631, 281–309.Google Scholar
Fage, A. & Warsap, J. H.1929 The effects of turbulence and surface roughness on the drag of a circular cylinder. Tech. Rep. 1283. Reports and Memoranda.Google Scholar
Güven, O., Farell, C. & Patel, V. C. 1980 Surface-roughness effects on the mean flow past circular cylinders. J. Fluid Mech. 98, 673–701.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Kravchenko, A. G. & Moin, P. 2000 Numerical studies of flow over a circular cylinder at Re D = 3900. Phys. Fluids 12, 403–417.Google Scholar
Lehmkuhl, O., Rodriguez, I., Borrell, R., Chiva, J. & Oliva, A. 2014 Unsteady forces on a circular cylinder at critical Reynolds numbers. Phys. Fluids 26, 4904415.Google Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9, 2443–2454.Google Scholar
Mittal, R. & Balachandar, S. 1996 Direct numerical simulation of flow past elliptic cylinders. J. Comput. Phys. 124, 351–367.Google Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10, 345–356.Google Scholar
Sayadi, T., Hamman, C. W. & Moin, P. 2013 Direct numerical simulation of complete H-type and K-type transitions with implications for the dynamics of turbulent boundary layers. J. Fluid Mech. 724, 480–509.Google Scholar
Schewe, G. 1983 On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 133, 265–285.Google Scholar
Sherman, F. S. 1990 Viscous Flow. McGraw-Hill.Google Scholar
Son, J. S. & Hanratty, T. J. 1969 Velocity gradients at the wall for flow around a cylinder at Reynolds numbers from 5 × 103 to 105 . J. Fluid Mech. 35, 353–368.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one finite and two periodic directions. J. Comput. Phys. 96, 297–324.Google Scholar
Szechenyi, E. 1975 Supercritical Reynolds number simulation for two-dimensional flow over circular cylinders. J. Fluid Mech. 70, 529–542.Google Scholar
Thwaites, B. 1949 Approximate calculation of the laminar boundary layer. Aeronaut. Q. 1, 245–280.Google Scholar
Voelkl, T., Pullin, D. I. & Chan, D. C. 2000 A physical-space version of the stretched-vortex subgrid-stress model for large-eddy simulation. Phys. Fluids 228, 2426–2442.Google Scholar
Weidman, P.1968 Wake transition and blockage effects on cylinder base pressures. PhD thesis, California Institute of Technology.Google Scholar
Yamagishi, Y. & Oki, M. 2004 Effect of groove shape on flow characteristics around a circular cylinder with grooves. J. Vis. 7, 209–216.Google Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33.Google Scholar
Zhang, W., Cheng, W., Gao, W., Qamar, A. & Samtaney, R. 2015 Geometrical effects on the airfoil flow separation and transition. Comput. Fluids 15, 60–73.Google Scholar