Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T22:40:53.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation of passive scalar dispersion in an urban-like canopy

Published online by Cambridge University Press:  16 April 2013

D. A. Philips ,
R. Rossi  and
G. Iaccarino
D. A. Philips*
Affiliation:
Department of Mechanical Engineering, Stanford University, 488 Escondido Mall, Building 02-500, Stanford, CA 94305, USA
R. Rossi
Affiliation:
Dipartimento di Ingegneria Industriale, Universitá di Bologna, Viale Risorgimento 2, 40136 Bologna, Italy
G. Iaccarino
Affiliation:
Department of Mechanical Engineering, Stanford University, 488 Escondido Mall, Building 02-500, Stanford, CA 94305, USA
*
†Email address for correspondence: dphilips@cascadetechnologies.com
Get access Rights & Permissions [Opens in a new window]

Abstract

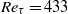Results from large-eddy simulations of short-range dispersion of a passive scalar from a point source release in an urban-like canopy are presented. The computational domain is that of a variable height array of buildings immersed in a pressure-driven, turbulent flow with a roughness Reynolds number ${\mathit{Re}}_{\tau } = 433$. A comparative study of several cases shows the changes in plume behaviour for different mean flow directions and source locations. The analysis of the results focuses on utilizing the high-fidelity datasets to examine the three-dimensional flow field and scalar plume structure. The detailed solution of the flow and scalar fields within the canopy allows for a direct assessment of the impact of local features of the building array geometry. The staggered, skewed and aligned arrangements of the buildings with respect to the oncoming flow were shown to affect plume development. Additional post-processing quantified this development through parameters fundamental to reduced-order Gaussian dispersion models. The parameters include measures of concentration decay with distance from the source as well as plume trajectory and spread. The horizontal plume trajectory and width were found to be more sensitive to source location variations, and hence local geometric features, than vertical plume parameters.

JFM classification

Turbulent Flows: Turbulence simulation Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 404 - 428
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biltoft, C 2001 Customer report for mock urban setting test. Tech. Rep. WDTC-FR-01-121. US Army Dugway Proving Ground, Dugway, UT.Google Scholar
Branford, S., Coceal, O., Thomas, T. & Belcher, S. 2011 Dispersion of a point-source release of a passive scalar through an urban-like array for different wind directions. Boundary-Layer Meteorol. 139, 367–394.CrossRefGoogle Scholar
Castro, I. P. & Robins, A. G. 1977 The flow around a surface-mounted cube in uniform and turbulent streams. J. Fluid Mech. 79 (2), 307–335.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104, 229–259.Google Scholar
Claus, J., Coceal, O., Thomas, T., Branford, S., Belcher, S. & Castro, I. 2012 Wind-direction effects on urban-type flows. Boundary-Layer Meteorol. 142, 265–287.Google Scholar
Coceal, O., Thomas, T., Castro, I. & Belcher, S. 2006 Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Boundary-Layer Meteorol. 121, 491–519.Google Scholar
Davidson, M. J., Mylne, K. R., Jones, C. D., Phillips, J. C., Perkins, R. J., Fung, J. C. H. & Hunt, J. C. R. 1995 Plume dispersion through large groups of obstacles: a field investigation. Atmos. Environ. 29 (22), 3245–3256.Google Scholar
Fernando, H. J. S., Zajic, D., Sabatino, S. Di, Dimitrova, R., Hedquist, B. & Dallman, A. 2010 Flow, turbulence, and pollutant dispersion in urban atmospheres. Phys. Fluids 22 (5), 051301.CrossRefGoogle Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A: Fluid Dyn. 3 (7), 1760–1765.Google Scholar
Hilderman, T. & Chong, R. 2007 A laboratory study of momentum and passive scalar transport and diffusion within and above a model urban canopy - final report. Tech. Rep. Document No. DRDC-Suffield-CR-2008-025. Defence R&D Canada, Suffield, Ralston, Alberta, 78 pp.Google Scholar
Hunt, J. C. R., Wray, A. & & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. Research Report CTR–S88. Center for Turbulence Research.Google Scholar
Iaccarino, G. & Ham, F. 2007 LES on Cartesian Grids with Anisotropic Refinement. In Complex Effects in Large Eddy Simulations (ed. Kassinos, S. C., Langer, C. A., Iaccarino, G. & Moin, P.). Lecture Notes in Computational Science and Engineering, vol. 56, pp. 219–233. Springer.CrossRefGoogle Scholar
Kang, Seongwon, Iaccarino, Gianluca & Ham, Frank 2009 Dns of buoyancy-dominated turbulent flows on a bluff body using the immersed boundary method. J. Comput. Phys. 228 (9), 3189–3208.CrossRefGoogle Scholar
MacDonald, R. W., Griffiths, R. F. & Cheah, S. C. 1997 Field experiments of dispersion through regular arrays of cubic structures. Atmosph. Environ. 31 (6), 783–795.Google Scholar
Mahesh, K., Constantinescu, G., Apte, S., Iaccarino, G., Ham, F. & Moin, P. 2006 Large-eddy simulation of reacting turbulent flows in complex geometries. Trans. ASME J. Appl. Mech. 73 (3), 374–381.Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197 (1), 215–240.Google Scholar
Moin, Parviz 2002 Advances in large eddy simulation methodology for complex flows. Intl J. Heat Fluid Flow 23 (5), 710–720.Google Scholar
Moin, P., Squires, K., Cabot, W. & Lee, S. 1991 A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids A: Fluid Dyn. 3 (11), 2746–2757.CrossRefGoogle Scholar
Oke, T. R. 1988 The urban energy balance. Prog. Phys. Geog. 12 (4), 471–508.CrossRefGoogle Scholar
Pasquill, F. & Smith, F. B. 1983 Atmospheric diffusion. In Ellis Horwood Series in Environmental Science, 3rd edn. Ellis Horwood.Google Scholar
Piomelli, U., Kang, S., Ham, F. & Iaccarino, G. 2006 Effect of discontinuous filter width in large-eddy simulations of plane channel flow. In Proceedings of the Summer Program, Center for Turbulence Research, pp. 151–162. Stanford.Google Scholar
Richter, David, Iaccarino, Gianluca & Shaqfeh, Eric, S. G. 2010 Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate reynolds numbers. J. Fluid Mech. 651, 415–442.Google Scholar
Rossi, R., Philips, D. A. & Iaccarino, G. 2010 A numerical study of scalar dispersion downstream of a wall-mounted cube using direct simulations and algebraic flux models. Intl J. Heat Fluid Flow 31 (5), 805–819.CrossRefGoogle Scholar
Rotach, M. W. 1993 Turbulence close to a rough urban surface part I: Reynolds stress. Boundary-Layer Meteorol. 65, 1–28.CrossRefGoogle Scholar
United States Environmental Protection Agency, 2012 Technology Transfer Network Support Centre for Regulatory Atmospheric Modelling: Preferred/recommended modelshttp://www.epa.gov/scram001/dispersion_prefrec.htm.Google Scholar
Vanella, M., Piomelli, U. & Balaras, E. 2008 Effect of grid discontinuities on large-eddy simulation statistics and flow fields. J. Turbul. 9, N32.CrossRefGoogle Scholar
Wang, B.-C., Yee, E. & Lien, F.-S. 2009 Numerical study of dispersing pollutant clouds in a built-up environment. Intl J. Heat Fluid Flow 30 (1), 3–19.CrossRefGoogle Scholar
Xie, Z. & Castro, I. 2006 LES and RANS for turbulent flow over arrays of wall-mounted obstacles. Flow Turbul. Combust. 76, 291–312.CrossRefGoogle Scholar
Xie, Z., Coceal, O. & Castro, I. 2008 Large-eddy simulation of flows over random urban-like obstacles. Boundary-Layer Meteorol. 129, 1–23.CrossRefGoogle Scholar
Yee, E. & Biltoft, C. A. 2004 Concentration fluctuation measurements in a plume dispersing through a regular array of obstacles. Boundary-Layer Meteorol. 111, 363–415.Google Scholar