Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T02:06:12.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer

Published online by Cambridge University Press:  11 November 2015

W. Cheng ,
D. I. Pullin  and
R. Samtaney
W. Cheng*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
R. Samtaney
Affiliation:
Mechanical Engineering, Physical Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
*
†Email address for correspondence: chengw@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present large-eddy simulations (LES) of separation and reattachment of a flat-plate turbulent boundary-layer flow. Instead of resolving the near wall region, we develop a two-dimensional virtual wall model which can calculate the time- and space-dependent skin-friction vector field at the wall, at the resolved scale. By combining the virtual-wall model with the stretched-vortex subgrid-scale (SGS) model, we construct a self-consistent framework for the LES of separating and reattaching turbulent wall-bounded flows at large Reynolds numbers. The present LES methodology is applied to two different experimental flows designed to produce separation/reattachment of a flat-plate turbulent boundary layer at medium Reynolds number 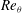$Re_{{\it\theta}}$ based on the momentum boundary-layer thickness 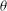${\it\theta}$. Comparison with data from the first case at 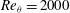$Re_{{\it\theta}}=2000$ demonstrates the present capability for accurate calculation of the variation, with the streamwise co-ordinate up to separation, of the skin friction coefficient, $Re_{{\it\theta}}$, the boundary-layer shape factor and a non-dimensional pressure-gradient parameter. Additionally the main large-scale features of the separation bubble, including the mean streamwise velocity profiles, show good agreement with experiment. At the larger 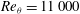$Re_{{\it\theta}}=11\,000$ of the second case, the LES provides good postdiction of the measured skin-friction variation along the whole streamwise extent of the experiment, consisting of a very strong adverse pressure gradient leading to separation within the separation bubble itself, and in the recovering or reattachment region of strongly-favourable pressure gradient. Overall, the present two-dimensional wall model used in LES appears to be capable of capturing the quantitative features of a separation-reattachment turbulent boundary-layer flow at low to moderately large Reynolds numbers.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , pp. 78 - 108
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Mizobuchi, Y., Matsuo, Y. & Spalart, P. R. 2012 DNS and modeling of a turbulent boundary layer with separation and reattachment over a range of Reynolds numbers. In Annual Research Briefs, pp. 311–322. Center for Turbulence Research.Google Scholar
Alving, A. E. & Fernholz, H. H. 1996 Turbulence measurements around a mild separation bubble and downstream of reattachment. J. Fluid Mech. 322, 297–328.Google Scholar
Bose, S. T. & Moin, P. 2014 A dynamic slip boundary condition for wall-modeled large-eddy simulation. Phys. Fluids 26, 015104.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Cheng, W. & Samtaney, R. 2014 Power-law versus log-law in wall-bounded turbulence: a large-eddy simulation perspective. Phys. Fluids 26, 011703.Google Scholar
Chung, D. & Pullin, D. I. 2009 Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 631, 281–309.Google Scholar
Constantinescu, G. & Squires, K. D. 2004 Numerical investigations of flow over a sphere in the subcritical and supercritical regimes. Phys. Fluids 16, 1449–1466.Google Scholar
Inoue, M., Mathis, R., Marusic, I. & Pullin, D. I. 2012 Inner-layer intensities for the flat-plate turbulent boundary layer combining a predictive wall-model with large-eddy simulations. Phys. Fluids 24 (7), 075102.Google Scholar
Inoue, M. & Pullin, D. I. 2011 Large-eddy simulation of the zero pressure gradient turbulent boundary layer up to $Re_{{\it\theta}}={\mathcal{O}}(10^{12})$ . J. Fluid Mech. 686, 507–533.Google Scholar
Inoue, M., Pullin, D. I., Harun, Z. & Marusic, I. 2013 LES of the adverse-pressure gradient turbulent boundary layer. Intl J. Heat Fluid Flow 44, 293–300.Google Scholar
Lögdberg, O., Angele, K. & Alfredsson, P. 2008 On the scaling of turbulent separating boundary layers. Phys. Fluids 20, 075104.CrossRefGoogle Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.Google Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25, 2193–2203.Google Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9, 2443–2454.CrossRefGoogle Scholar
Na, Y. & Moin, P. 1998 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.Google Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Patrick, W.1987, Mean flowfield measurements in a separated and reattached flat-plate turbulent boundary layer. NASA Contractor Rep. 4052.Google Scholar
Perot, J. B. 1993 An analysis of the fractional step method. J. Comput. Phys. 108, 51–58.Google Scholar
Perry, A. E. & Fairlie, B. D. 1975 A study of turbulent boundary-layer separation and reattachment. J. Fluid Mech. 69, 657–672.Google Scholar
Perry, A. E. & Schofield, W. H. 1973 Mean velocity and shear stress distributions in turbulent boundary layers. Phys. Fluids 16 (12), 2068–2074.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.Google Scholar
Saito, N. & Pullin, D. I. 2014 Large eddy simulation of smooth–rough–smooth transitions in turbulent channel flows. Intl J. Heat Mass Transfer 78, 707–720.Google Scholar
Saito, N., Pullin, D. I. & Inoue, M. 2012 Large eddy simulation of smooth-wall, transitional and fully rough-wall channel flow. Phys. Fluids 24 (7), 075103.Google Scholar
Sanborn, V. A. & Kline, S. J. 1961 Flow models in boundary-layer stall inception. J. Fluids Engng 83 (3), 317–327.Google Scholar
Simpson, R. L. 1983 A model for the backflow mean velocity profile. AIAA J. 21 (1), 142–143.Google Scholar
Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21 (1), 205–232.Google Scholar
Simpson, R. L., Chew, Y. T. & Shivaprasad, B. G. 1981a The structure of a separating turbulent boundary-layer. Part 1. Mean flow and Reynolds stresses. J. Fluid Mech. 113, 23–51.Google Scholar
Simpson, R. L., Chew, Y. T. & Shivaprasad, B. G. 1981b The structure of a separating turbulent boundary-layer. Part 2. Higher-order turbulence results. J. Fluid Mech. 113, 53–73.CrossRefGoogle Scholar
Simpson, R. L., Strickland, J. H. & Barr, P. W. 1977 Features of a separating turbulent boundary-layer in vicinity of separation. J. Fluid Mech. 79, 553–594.Google Scholar
Skote, M.2001 Studies of turbulent boundary layer flow through direct numerical simulation. PhD thesis, Royal Institute of Technology.Google Scholar
Skote, M. & Henningson, D. S. 2002 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.Google Scholar
Spalart, P. R. 2009 Detached-eddy simulation. Annu. Rev. Fluid Mech. 41, 181–202.Google Scholar
Spalart, P. R. & Coleman, G. N. 1997 Numerical study of a separation bubble with heat transfer. Eur. J. Mech. (B/Fluids) 16 (2), 169–189.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one finite and two periodic directions. J. Comput. Phys. 96, 297–324.Google Scholar
Voelkl, T., Pullin, D. I. & Chan, D. C. 2000 A physical-space version of the stretched-vortex subgrid-stress model for large-eddy simulation. Phys. Fluids 228, 2426–2442.Google Scholar