Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alfredsson, P. Henrik
Örlü, Ramis
and
Segalini, Antonio
2012.
A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows.
European Journal of Mechanics - B/Fluids,
Vol. 36,
Issue. ,
p.
167.
Schlatter, Philipp
and
Örlü, Ramis
2012.
Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects.
Journal of Fluid Mechanics,
Vol. 710,
Issue. ,
p.
5.
Inoue, M.
Mathis, R.
Marusic, I.
and
Pullin, D. I.
2012.
Inner-layer intensities for the flat-plate turbulent boundary layer combining a predictive wall-model with large-eddy simulations.
Physics of Fluids,
Vol. 24,
Issue. 7,
Saito, Namiko
Pullin, Dale I.
and
Inoue, Michio
2012.
Large eddy simulation of smooth-wall, transitional and fully rough-wall channel flow.
Physics of Fluids,
Vol. 24,
Issue. 7,
Pullin, D. I.
Inoue, M.
and
Saito, N.
2013.
On the asymptotic state of high Reynolds number, smooth-wall turbulent flows.
Physics of Fluids,
Vol. 25,
Issue. 1,
Inoue, M.
Pullin, D.I.
Harun, Z.
and
Marusic, I.
2013.
LES of the adverse-pressure gradient turbulent boundary layer.
International Journal of Heat and Fluid Flow,
Vol. 44,
Issue. ,
p.
293.
Lee, Jungil
Cho, Minjeong
and
Choi, Haecheon
2013.
Large eddy simulations of turbulent channel and boundary layer flows at high Reynolds number with mean wall shear stress boundary condition.
Physics of Fluids,
Vol. 25,
Issue. 11,
Eitel-Amor, Georg
Örlü, Ramis
and
Schlatter, Philipp
2014.
Simulation and validation of a spatially evolving turbulent boundary layer up to.
International Journal of Heat and Fluid Flow,
Vol. 47,
Issue. ,
p.
57.
Encinar, M P
García-Mayoral, R
and
Jiménez, J
2014.
Scaling of velocity fluctuations in off-wall boundary conditions for turbulent flows.
Journal of Physics: Conference Series,
Vol. 506,
Issue. ,
p.
012002.
Dhamankar, Nitin S.
Martha, Chandra Sekhar
Situ, Yingchong
Aikens, Kurt M.
Blaisdell, Gregory A.
Lyrintzis, Anastasios S.
and
Li, Zhiyuan
2014.
Digital Filter-based Turbulent Inflow Generation for Jet Aeroacoustics on Non-Uniform Structured Grids.
Cheng, Wan
and
Samtaney, Ravi
2014.
A high-resolution code for large eddy simulation of incompressible turbulent boundary layer flows.
Computers & Fluids,
Vol. 92,
Issue. ,
p.
82.
Cheng, W.
and
Samtaney, R.
2014.
Power-law versus log-law in wall-bounded turbulence: A large-eddy simulation perspective.
Physics of Fluids,
Vol. 26,
Issue. 1,
Chung, Daniel
and
Matheou, Georgios
2014.
Large-Eddy Simulation of Stratified Turbulence. Part I: A Vortex-Based Subgrid-Scale Model.
Journal of the Atmospheric Sciences,
Vol. 71,
Issue. 5,
p.
1863.
Xu, Lei
Rusak, Zvi
and
Castillo, Luciano
2014.
A Reduced-Order Model of the Mean Properties of a Turbulent Wall Boundary Layer at a Zero Pressure Gradient.
Journal of Fluids Engineering,
Vol. 136,
Issue. 3,
Yang, X. I. A.
Sadique, J.
Mittal, R.
and
Meneveau, C.
2015.
Integral wall model for large eddy simulations of wall-bounded turbulent flows.
Physics of Fluids,
Vol. 27,
Issue. 2,
Mankbadi, Mina R.
DeBonis, James R.
and
Georgiadis, Nicholas J.
2015.
Comparison of High-Order and Low-Order Methods for Large-Eddy Simulation of a Compressible Shear Layer.
Cheng, W.
Pullin, D. I.
and
Samtaney, R.
2015.
Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 785,
Issue. ,
p.
78.
Castro, Ian P.
2015.
Turbulence intensity in wall-bounded and wall-free flows.
Journal of Fluid Mechanics,
Vol. 770,
Issue. ,
p.
289.
Park, George Ilhwan
and
Moin, Parviz
2016.
Space-time characteristics of wall-pressure and wall shear-stress fluctuations in wall-modeled large eddy simulation.
Physical Review Fluids,
Vol. 1,
Issue. 2,
Sridhar, A.
Pullin, D. I.
and
Cheng, W.
2017.
Rough-wall turbulent boundary layers with constant skin friction.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
26.
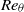 based on the free-stream velocity and the momentum thickness in the range
based on the free-stream velocity and the momentum thickness in the range 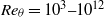 . Results include the inverse square-root skin-friction coefficient,
. Results include the inverse square-root skin-friction coefficient, 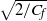 , velocity profiles, the shape factor
, velocity profiles, the shape factor 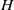 , the von Kármán ‘constant’ and the Coles wake factor as functions of
, the von Kármán ‘constant’ and the Coles wake factor as functions of 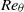 . Comparisons with some direct numerical simulation (DNS) and experiment are made including turbulent intensity data from atmospheric-layer measurements at
. Comparisons with some direct numerical simulation (DNS) and experiment are made including turbulent intensity data from atmospheric-layer measurements at 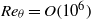 . At extremely large
. At extremely large 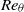 , the empirical Coles–Fernholz relation for skin-friction coefficient provides a reasonable representation of the LES predictions. While the present LES methodology cannot probe the structure of the near-wall region, the present results show turbulence intensities that scale on the wall-friction velocity and on the Clauser length scale over almost all of the outer boundary layer. It is argued that LES is suggestive of the asymptotic, infinite Reynolds number limit for the smooth-wall turbulent boundary layer and different ways in which this limit can be approached are discussed. The maximum
, the empirical Coles–Fernholz relation for skin-friction coefficient provides a reasonable representation of the LES predictions. While the present LES methodology cannot probe the structure of the near-wall region, the present results show turbulence intensities that scale on the wall-friction velocity and on the Clauser length scale over almost all of the outer boundary layer. It is argued that LES is suggestive of the asymptotic, infinite Reynolds number limit for the smooth-wall turbulent boundary layer and different ways in which this limit can be approached are discussed. The maximum 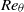 of the present simulations appears to be limited by machine precision and it is speculated, but not demonstrated, that even larger
of the present simulations appears to be limited by machine precision and it is speculated, but not demonstrated, that even larger 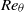 could be achieved with quad- or higher-precision arithmetic.
could be achieved with quad- or higher-precision arithmetic.