Article contents
Large-eddy simulation-based reconstruction of turbulence in a neutral boundary layer using spectral-tensor regularization
Published online by Cambridge University Press: 27 February 2024
Abstract
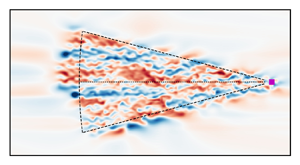
We propose an efficient method to reconstruct the turbulent flow field in a neutrally stratified atmospheric boundary layer using large-eddy simulation (LES) and a series of lidar measurements. The reconstruction is formulated as a strong four-dimensional variational data assimilation problem, which involves optimizing two competing terms that contribute in the objective functional. The first term is a likelihood term, while the second contains the initial background distribution of turbulent velocity fluctuations and works as a regularization term. However, computing and storing the full background covariance tensor in turbulent flows is time consuming and resource intensive. In the current work, we investigate the possibility of replacing the complex background tensor by simple analytical approximations based on spectral tensors such as the Hunt–Graham–Wilson (HGW) model (Boundary-Layer Meteorol., vol. 85, 1997, pp. 35–52) or the Mann model (J. Fluid Mech., vol. 273, 1994, pp. 141–168). Afterwards, the problem is solved using a quasi-Newton algorithm and preconditioned to enhance the convergence rate. We test the method using virtual lidar measurements collected on a fine reference LES. Results show a super-linear convergence rate of the optimization algorithm to a local minimum and very good agreement between virtual lidar measurements and reconstruction in the scanning region. Furthermore, we demonstrate that incorporating the Saffman energy spectrum ( $E(k) \sim k^2$ where E is the energy spectrum and k is the magnitude of the wavenumber vector) at low wavenumbers into the Mann spectral tensor yields a longer streamwise correlation length, resulting in reduced reconstruction error when compared with the Batchelor spectrum (
$E(k) \sim k^2$ where E is the energy spectrum and k is the magnitude of the wavenumber vector) at low wavenumbers into the Mann spectral tensor yields a longer streamwise correlation length, resulting in reduced reconstruction error when compared with the Batchelor spectrum ( $E(k) \sim k^4$). Finally, we observe that using the HGW model or Mann model with a Saffman spectrum yields similar results.
$E(k) \sim k^4$). Finally, we observe that using the HGW model or Mann model with a Saffman spectrum yields similar results.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 3
- Cited by


