Article contents
Large-scale coherent structures in turbulent channel flow: a detuned instability of wall streaks
Published online by Cambridge University Press: 10 October 2024
Abstract
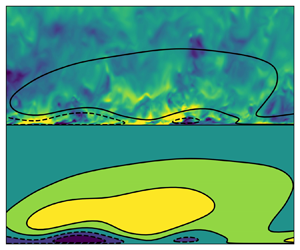
In this paper it is shown that a modal detuned instability of periodic near-wall streaks originates a large-scale structure in the bulk of the turbulent channel flow. The effect of incoherent turbulent fluctuations is included in the linear operator by means of an eddy viscosity. The base flow is an array of periodic two-dimensional streaks, extracted from numerical simulations in small domains, superposed to the turbulent mean profile. The stability problem for a large number of periodic units is efficiently solved using the block-circulant matrix method proposed by Schmid et al. (Phys. Rev. Fluids, vol. 2, 2017, 113902). For friction Reynolds numbers equal or higher than  $590$, it is shown that an unstable branch is present in the eigenspectra. The most unstable eigenmodes display large-scale modulations whose characteristic wavelengths are compatible with the large-scale end of the premultiplied velocity fluctuation spectra reported in previous computational studies. The wall-normal location of the large-wavelength near-wall peak in the spanwise spectrum of the eigenmode exhibits a power-law dependence on the friction Reynolds number, similarly to that found in experiments of pipes and boundary layers. Lastly, the shape of the eigenmode in the streamwise-wall-normal plane is reminiscent of the superstructures reported in the recent experiments of Deshpande et al. (J. Fluid Mech., vol. 969, 2023, A10). Therefore, there is evidence that such large-wavelength instabilities generate large-scale motions in wall-bounded turbulent flows.
$590$, it is shown that an unstable branch is present in the eigenspectra. The most unstable eigenmodes display large-scale modulations whose characteristic wavelengths are compatible with the large-scale end of the premultiplied velocity fluctuation spectra reported in previous computational studies. The wall-normal location of the large-wavelength near-wall peak in the spanwise spectrum of the eigenmode exhibits a power-law dependence on the friction Reynolds number, similarly to that found in experiments of pipes and boundary layers. Lastly, the shape of the eigenmode in the streamwise-wall-normal plane is reminiscent of the superstructures reported in the recent experiments of Deshpande et al. (J. Fluid Mech., vol. 969, 2023, A10). Therefore, there is evidence that such large-wavelength instabilities generate large-scale motions in wall-bounded turbulent flows.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 3
- Cited by


