Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T01:38:57.228Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear instability analysis of convection in a laterally heated cylinder

Published online by Cambridge University Press:  17 April 2014

Bo-Fu Wang ,
Zhen-Hua Wan ,
Zhi-Wei Guo ,
Dong-Jun Ma  and
De-Jun Sun
Bo-Fu Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, Anhui, PR China School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, Hubei, PR China
Zhen-Hua Wan
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, Anhui, PR China
Zhi-Wei Guo*
Affiliation:
School of Water Resources and Hydropower Engineering, Wuhan University, Wuhan 430072, Hubei, PR China
Dong-Jun Ma*
Affiliation:
National Space Science Center, Chinese Academy of Sciences, Beijing 100190, PR China
De-Jun Sun*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, Anhui, PR China
*
†Email addresses for correspondence: juice@mail.ustc.edu.cn, mdj@ustc.edu.cn, dsun@ustc.edu.cn
†Email addresses for correspondence: juice@mail.ustc.edu.cn, mdj@ustc.edu.cn, dsun@ustc.edu.cn
†Email addresses for correspondence: juice@mail.ustc.edu.cn, mdj@ustc.edu.cn, dsun@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

The three-dimensional instabilities of axisymmetric flow are investigated in a laterally heated vertical cylinder by linear stability analysis. Heating is confined to a central zone on the sidewall of the cylinder, while other parts of the sidewall are insulated and both ends of the cylinder are cooled. The length of the heated zone equals the radius of the cylinder. For three different aspect ratios, 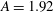$A= 1.92 $, 2, 2.1 (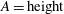$A=\mathrm{height}$/radius), the dependence of the critical Rayleigh number on the Prandtl number (from 0.02 to 6.7) has been studied in detail. For such a kind of laterally heated convection, some interesting stability results are obtained. A monotonous instability curve is obtained for 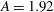$A= 1.92 $, while the instability curves for 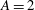$A= 2 $ and 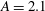$A= 2.1 $ are non-monotonous and multivalued. In particular, an instability island has been found for 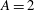$A=2$. Moreover, mechanisms corresponding to different instability results are obtained when the Prandtl number changes. At small Prandtl number, the flow is oscillatory unstable, which is dominated by hydrodynamic instability. At intermediate Prandtl number, the interaction between buoyancy and shear in the base flow plays a more important role than pure hydrodynamic instability. At even higher Prandtl number, Rayleigh–Bénard instability becomes the dominant process and the flow loses stability through steady bifurcation.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection Convection: Convection in cavities
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 447 - 459
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barwölff, G., König, F. & Seifert, G. 1997 Thermal buoyancy convection in vertical zone melting configurations. J. Appl. Math. Mech. 10, 757–766.Google Scholar
Baumgartl, J., Budweiser, W., Mueller, G. & Neumann, G. 1989 Studies of buoyancy driven convection in a vertical cylinder with parabolic temperature profile. J. Cryst. Growth 97, 9–17.Google Scholar
Borońska, K. & Tuckerman, L. S. 2006 Standing and travelling waves in cylindrical Rayleigh–Bénard convection. J. Fluid Mech. 559, 279–298.Google Scholar
Boussinesq, J. 1903 Théorie Analytique de la Chaleur, vol. 2. Gauthier–Villars.Google Scholar
Braunsfurth, M. G. & Mullin, T. 1996 An experimental study of oscillatory convection in liquid gallium. J. Fluid Mech. 327, 199–219.Google Scholar
Buell, J. C. & Catton, I. 1983 The effect of wall conduction on the stability of a fluid in a right circular cylinder heated from below. Trans. ASME J. Heat Transfer 105, 255–260.Google Scholar
Charlson, G. S. & Sani, R. L. 1970 Thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 13, 1479–1496.Google Scholar
Charlson, G. S. & Sani, R. L. 1971 On thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 14, 2157–2160.Google Scholar
Chen, J. G., Chen, H. X., Zhang, G. H. & Fu, S. 2006 Stability of flow between rotating cylinders with axial buoyancy effect. Sci. China Phys. Mech. Astron. 49, 564–575.Google Scholar
Daniels, K. E., Brausch, O., Pesch, W. & Bodenschatz, E. 2008 Competition and bistability of ordered undulations and undulation chaos in inclined layer convection. J. Fluid Mech. 597, 261–282.Google Scholar
Daniels, K. E., Plapp, B. B. & Bodenschatz, E. 2003 Pattern formation in inclined layer convection. Phys. Rev. Lett. 84, 5320–5323.Google Scholar
Erenburg, V., Gelfgat, A. Yu., Kit, E., Bar-Yoseph, P. Z. & Solan, A. 2003 Multiple states, stability and bifurcations of natural convection in a rectangular cavity with partially heated vertical walls. J. Fluid Mech. 492, 63–89.CrossRefGoogle Scholar
Gelfgat, A. Yu., Bar-Yoseph, P. Z. & Solan, A. 2000 Axisymmetry breaking instabilities of natural convection in a vertical Bridgman growth configuration. J. Cryst. Growth 220, 316–325.Google Scholar
Gelfgat, A. Yu., Bar-Yoseph, P. Z. & Yarin, A. L. 1997 On oscillatory instability of convective flows at low Prandtl number. Trans. ASME J. Fluids Engng. 119, 823–830.Google Scholar
Gelfgat, A. Yu., Bar-Yoseph, P. Z. & Yarin, A. L. 1999 Stability of multiple steady states of convection in laterally heated cavities. J. Fluid Mech. 388, 315–334.Google Scholar
Gemeny, L. E., Martin Witkowski, L. & Walker, J. S. 2007 Buoyant instability in a laterally heated vertical cylinder. Intl J. Heat Mass Transfer 50, 1010–1017.CrossRefGoogle Scholar
Hardin, G. R., Sani, R. L., Henry, D. & Roux, B. 1990 Buoyancy-driven instability in a vertical cylinder: Binary fluids with Soret effect. Part 1. General-theory and stationary stability results. Intl J. Numer. Meth. Fluids 10 (1), 79–117.Google Scholar
Hurle, D. T. J. 1966 Temperature oscillations in molten metals and their relationship to growth striae in melt-grown crystals. Phil. Mag. 13, 305–310.Google Scholar
Jaluria, Y. 2001 Fluid flow phenomena in materials processing: the 2000 Freeman scholar lecture. Trans. ASME J. Fluids Engng. 123, 173–210.CrossRefGoogle Scholar
Knoll, D. A. & Keyes, D. E. 2004 Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J. Comput. Phys. 193, 357–397.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C.(Eds.) 1998 ARPACK Users Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.Google Scholar
Ma, D. J., Henry, D. & BenHadid, H. 2005 Three-dimensional numerical study of natural convection in vertical cylinders partially heated from the side. Phys. Fluids 17, 124101.CrossRefGoogle Scholar
Ma, D. J., Sun, D. J. & Yin, X. Y. 2006 Multiplicity of steady states in cylindrical Rayleigh–Bénard convection. Phys. Rev. E 74, 037302.CrossRefGoogle ScholarPubMed
Meseguer, A. & Marques, F. 2000 On the competition between centrifugal and shear instability in spiral Couette flow. J. Fluid Mech. 402, 33–56.Google Scholar
Meseguer, A. & Marques, F. 2002 On the competition between centrifugal and shear instability in spiral Poiseuille flow. J. Fluid Mech. 455, 129–148.Google Scholar
Müller, G. 1993 Convective instabilities in melt growth configurations. J. Cryst. Growth 128, 26–36.Google Scholar
Müller, G. & Ostrogorsky, A. 1994 Convection in melt growth. In Handbook of Crystal Growth (ed. Hurle, D. T. J.), vol. 2, pp. 711–781. North-Holland.Google Scholar
Neumann, G. 1990 Three-dimensional numerical simulation of buoyancy-driven convection in vertical cylinders heated from below. J. Fluid Mech. 214, 559–578.Google Scholar
Oberbeck, A. 1879 Über die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 7, 271–292.Google Scholar
Peng, J. & Zhu, K. Q. 2004 Linear stability of Bingham fluids in spiral Couette flow. J. Fluid Mech. 512, 21–45.CrossRefGoogle Scholar
Rubinov, A., Erenburg, V., Gelfgat, A. Yu., Kit, E., Bar-Yoseph, P. Z. & Solan, A. 2004 Three-dimensional instabilities of natural convection flow in a vertical cylinder with partially heated sidewall. Trans. ASME J. Heat Transfer 126, 586–599.Google Scholar
Selver, R., Kamotani, Y. & Ostrach, S. 1998 Natural convection of a liquid metal in vertical cylinders heated locally from the side. Trans. ASME J. Heat Transfer 120, 108–114.Google Scholar
Stork, K. & Müller, U. 1975 Convection in boxes: an experimental investigation in vertical cylinders and annuli. J. Fluid Mech. 71, 231–240.Google Scholar
Touihri, R., Ben Hadid, H. & Henry, D. 1999 On the onset of convective instabilities in cylindrical cavities heated from below. I. Pure thermal case. Phys. Fluids 11, 2078–2088.Google Scholar
Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for time-steppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems (ed. Doedel, E. & Tuckerman, L. S.), vol. 119, pp. 453–466. Springer.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for the three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.CrossRefGoogle Scholar
Wang, B. F., Ma, D. J., Chen, C. & Sun, D. J. 2012 Linear stability analysis of cylindrical Rayleigh–Bénard convection. J. Fluid Mech. 38, 27–39.Google Scholar
Wanschura, M., Kuhlmann, H. C. & Rath, H. J. 1996 Three-dimensional instability of axisymmetric buoyant convection in cylinders heated from below. J. Fluid Mech. 326, 399–415.CrossRefGoogle Scholar