Published online by Cambridge University Press: 01 October 2019
The influence of turbulence characteristics of a cross-airflow including its velocity fluctuations and integral length and time scales on the primary breakup regime, trajectory and breakup height and time of a transversely injected liquid jet was investigated experimentally. Turbulence intensity of the incoming airflow was varied from 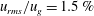 $u_{rms}/u_{g}=1.5\,\%$ to 5.5 % (where
$u_{rms}/u_{g}=1.5\,\%$ to 5.5 % (where 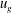 $u_{g}$ is cross-airflow streamwise mean velocity and
$u_{g}$ is cross-airflow streamwise mean velocity and 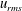 $u_{rms}$ is the r.m.s. of the corresponding cross-airflow streamwise mean velocity fluctuation) by placing at the inlet of the test section a perforated plate/grid with a solidity ratio of
$u_{rms}$ is the r.m.s. of the corresponding cross-airflow streamwise mean velocity fluctuation) by placing at the inlet of the test section a perforated plate/grid with a solidity ratio of 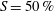 $S=50\,\%$. Over the range of gas Weber number,
$S=50\,\%$. Over the range of gas Weber number, 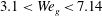 $3.1<We_{g}<7.14$, the ensuing liquid jet exhibited more fluctuations and late breakup transitional behaviour under turbulent airflow conditions than in a uniform cross-airflow. Proper orthogonal decomposition of the liquid jet dynamics revealed that the use of grid caused a rise in the wavelength of travelling waves along the liquid jet, which hindered the transition of the liquid jet primary breakup regime from enhanced capillary breakup to the bag breakup mode. The quantitative results demonstrated that, at a constant airflow mean velocity, turbulent cross-airflow caused the liquid jet to bend earlier compared with its uniform counterpart. A power-law empirical correlation was proposed for the prediction of the liquid jet trajectory which takes into account the effect of turbulent Reynolds number. The liquid jet breakup height (in the
$3.1<We_{g}<7.14$, the ensuing liquid jet exhibited more fluctuations and late breakup transitional behaviour under turbulent airflow conditions than in a uniform cross-airflow. Proper orthogonal decomposition of the liquid jet dynamics revealed that the use of grid caused a rise in the wavelength of travelling waves along the liquid jet, which hindered the transition of the liquid jet primary breakup regime from enhanced capillary breakup to the bag breakup mode. The quantitative results demonstrated that, at a constant airflow mean velocity, turbulent cross-airflow caused the liquid jet to bend earlier compared with its uniform counterpart. A power-law empirical correlation was proposed for the prediction of the liquid jet trajectory which takes into account the effect of turbulent Reynolds number. The liquid jet breakup height (in the 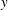 $y$-axis direction) normalized by the jet diameter, and accordingly the liquid jet breakup time normalized by the airflow integral time scale, were found to decrease with increasing the airflow turbulence intensity. Two power-law empirical correlations were proposed to predict the liquid jet breakup height and time.
$y$-axis direction) normalized by the jet diameter, and accordingly the liquid jet breakup time normalized by the airflow integral time scale, were found to decrease with increasing the airflow turbulence intensity. Two power-law empirical correlations were proposed to predict the liquid jet breakup height and time.
Present address: Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON M5S 3G8, Canada.