Article contents
Liquid rope coiling: a synoptic view
Published online by Cambridge University Press: 28 December 2016
Abstract
In liquid rope coiling, a slender jet of viscous fluid falling onto a rigid surface builds a rotating corkscrew-like structure. Here, I use a numerical continuation method to construct a complete regime diagram for liquid rope coiling. I first consider the onset of coiling, and show that a suitable onset criterion is that the radius
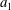 $a_{1}$
of the rope itself be just equal to the radius
$a_{1}$
of the rope itself be just equal to the radius
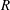 $R$
of the coil. Numerical calculation of the critical surface
$R$
of the coil. Numerical calculation of the critical surface
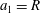 $a_{1}=R$
in the space of the dimensionless fall height
$a_{1}=R$
in the space of the dimensionless fall height
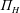 $\unicode[STIX]{x1D6F1}_{H}$
, flow rate
$\unicode[STIX]{x1D6F1}_{H}$
, flow rate
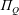 $\unicode[STIX]{x1D6F1}_{Q}$
and nozzle diameter
$\unicode[STIX]{x1D6F1}_{Q}$
and nozzle diameter
 $\unicode[STIX]{x1D6F1}_{d}$
shows that the surface has four distinct asymptotic limits corresponding to a viscous (V) mode, a gravitational (G) mode and two inertial modes (I1, I2) which are distinguished by how much the tail of the jet is stretched by gravity. Exact expressions for the onset frequencies in each of these four modes are determined. Finally, the regime diagram is constructed in the form of contour plots of the dimensionless coiling frequency as a function of
$\unicode[STIX]{x1D6F1}_{d}$
shows that the surface has four distinct asymptotic limits corresponding to a viscous (V) mode, a gravitational (G) mode and two inertial modes (I1, I2) which are distinguished by how much the tail of the jet is stretched by gravity. Exact expressions for the onset frequencies in each of these four modes are determined. Finally, the regime diagram is constructed in the form of contour plots of the dimensionless coiling frequency as a function of
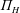 $\unicode[STIX]{x1D6F1}_{H}$
and
$\unicode[STIX]{x1D6F1}_{H}$
and
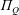 $\unicode[STIX]{x1D6F1}_{Q}$
for several values of
$\unicode[STIX]{x1D6F1}_{Q}$
for several values of
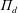 $\unicode[STIX]{x1D6F1}_{d}$
. The diagram exhibits a total of six modes: V, G, I1, I2, a multivalued inertio-gravitational (IG) mode and a third inertial mode I3 with viscosity-dominated stretching of the tail. The regime diagram permits prediction of the coiling frequency for given values of the fall height, flow rate, viscosity and nozzle diameter, and should therefore be useful in practical applications ranging from non-woven textile production to 3D printing.
$\unicode[STIX]{x1D6F1}_{d}$
. The diagram exhibits a total of six modes: V, G, I1, I2, a multivalued inertio-gravitational (IG) mode and a third inertial mode I3 with viscosity-dominated stretching of the tail. The regime diagram permits prediction of the coiling frequency for given values of the fall height, flow rate, viscosity and nozzle diameter, and should therefore be useful in practical applications ranging from non-woven textile production to 3D printing.
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 22
- Cited by



