Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T05:28:26.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Local linear stability of laminar axisymmetric plumes

Published online by Cambridge University Press:  04 September 2015

R. V. K. Chakravarthy ,
L. Lesshafft  and
P. Huerre
R. V. K. Chakravarthy
Affiliation:
Laboratoire d’Hydrodynamique, CNRS/École polytechnique, 91128 Palaiseau CEDEX, France
L. Lesshafft*
Affiliation:
Laboratoire d’Hydrodynamique, CNRS/École polytechnique, 91128 Palaiseau CEDEX, France
P. Huerre
Affiliation:
Laboratoire d’Hydrodynamique, CNRS/École polytechnique, 91128 Palaiseau CEDEX, France
*
†Email address for correspondence: lesshafft@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The temporal and spatiotemporal stability of thermal plumes is investigated for laminar velocity and temperature profiles, under the Boussinesq approximation, in the far self-similar region as well as in the region close to a finite-size inlet. In the self-similar case, Prandtl and Grashof numbers are systematically varied, and azimuthal wavenumbers 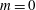$m=0$, 1 and 2 are considered. In the temporal analysis, helical modes of 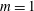$m=1$ are found to be dominant throughout the unstable parameter space, with few exceptions. Axisymmetric modes typically present smaller growth rates, but they may dominate at very low Prandtl and Grashof numbers. Double-helical modes of 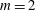$m=2$ are unstable over a very restricted range of parameters. Only the helical 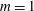$m=1$ mode is found to ever become absolutely unstable, whereas 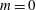$m=0$ and 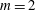$m=2$ modes are at most convectively unstable. In a temporal setting, an analysis of the perturbation energy growth identifies buoyancy- and shear-related mechanisms as the two potentially destabilizing flow ingredients. Buoyancy is demonstrated to be important at low Grashof numbers and long wavelengths, whereas classical shear mechanisms are dominant at high Grashof numbers and shorter wavelengths. The physical mechanism of destabilization through the effect of buoyancy is investigated, and an interpretation is proposed. In the near-source region, both axisymmetric and helical modes may be unstable in a temporal sense over a significant range of wavenumbers. However, absolute instability is again only found for helical 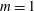$m=1$ modes.

JFM classification

Instability: Absolute/convective instability Convection: Buoyancy-driven instability Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 344 - 369
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14, 529–551.Google Scholar
Brand, R. S. & Lahey, F. J. 1967 The heated laminar vertical jet. J. Fluid Mech. 29 (2), 305–315.Google Scholar
Cetegen, B. M., Dong, Y. & Soteriou, M. C. 1998 Experiments on stability and oscillatory behaviour of planar buoyant plumes. Phys. Fluids 10 (7), 1658–1665.CrossRefGoogle Scholar
Cetegen, B. M. & Kasper, K. D. 1996 Experiments on the oscillatory behavior of buoyant plumes of helium and helium-air mixtures. Phys. Fluids 8 (11), 2974–2984.Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77 (02), 397–413.Google Scholar
Delbende, I., Chomaz, J.-M. & Huerre, P. 1998 Absolute/convective instabilities in the batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.Google Scholar
Deloncle, A.2007 Three dimensional instabilities in stratified fluids. PhD thesis, Ecole Polytechnique, Palaiseau, France.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
van Dyke, D. 1982 An Album of Fluid Motion. p. figure 107. Parabolic Press.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.CrossRefGoogle Scholar
Hattori, T., Bartos, N., Norris, S. E., Kirkpatrick, M. P. & Armfield, S. W. 2013 Simulation and analysis of puffing instability in the near field of pure thermal planar plumes. Intl J. Therm. Sci. 69, 1–13.Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.Google Scholar
Jiang, X. & Luo, K. H. 2000a Combustion-induced buoyancy effects of an axisymmetric reactive plume. Proc. Combust. Inst. 28 (2), 1989–1995.CrossRefGoogle Scholar
Jiang, X. & Luo, K. H. 2000b Direct numerical simulation of the puffing phenomenon of an axisymmetric thermal plume. Theoret. Comput. Fluid Dynamics 14, 55–74.Google Scholar
Khorrami, M. R., Malik, M. R. & Ash, R. L. 1989 Application of spectral collocation techniques to the stability of swirling flows. J. Comput. Phys. 81, 206–229.CrossRefGoogle Scholar
Lesshafft, L. & Huerre, P. 2007 Linear impulse response in hot round jets. Phys. Fluids 19 (2), 024102.Google Scholar
Lesshafft, L., Huerre, P., Sagaut, P. & Terracol, M. 2006 Nonlinear global modes in hot jets. J. Fluid Mech. 554, 393–409.Google Scholar
Lesshafft, L. & Marquet, O. 2010 Optimal velocity and density profiles for the onset of absolute instability in jets. J. Fluid Mech. 662, 398–408.Google Scholar
Lombardi, M., Caulfield, C. P., Cossu, C., Pesci, A. I. & Goldstein, R. E. 2011 Growth and instability of a laminar plume in a strongly stratified environment. J. Fluid Mech. 671, 184–206.CrossRefGoogle Scholar
Lopez, J. M. & Marques, F. 2013 Instability of plumes driven by localized heating. J. Fluid Mech. 736, 616–640.Google Scholar
Maxworthy, T. 1999 The flickering candle: transition to a global oscillation in a thermal plume. J. Fluid Mech. 390, 297–323.CrossRefGoogle Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluid Mech. 660, 499–526.Google Scholar
Mollendorf, J. C. & Gebhart, B. 1973 An experimental and numerical study of the viscous stability of a round laminar vertical jet with and without thermal buoyancy for symmetric and asymmetric perturbations. J. Fluid Mech. 61 (2), 367–399.Google Scholar
Monkewitz, P. & Sohn, K. 1988 Absolute instability in hot jets. AIAA 26, 911–916.Google Scholar
Nachtsheim, P. R.1963 Stability of free-convection boundary layer flows. NACA Tech. Rep. TN D-2089.Google Scholar
Nadal, F., Meunier, P., Pouligny, B. & Laurichesse, E. 2011 Stationary plume induced by carbon dioxide dissolution. J. Fluid Mech. 719, 203–229.Google Scholar
Pier, B. 2008 Local and global instabilities in the wake of a sphere. J. Fluid Mech. 603, 39–61.Google Scholar
Riley, D. S. & Tveitereid, M. 1984 On the stability of an axisymmetric plume in a uniform flow. J. Fluid Mech. 142, 171–186.Google Scholar
Satti, R. P. & Agrawal, A. K. 2004 Numerical analysis of flow evolution in a helium jet injected into ambient air. ASME 2, 1267–1276.Google Scholar
Satti, R. P. & Agrawal, A. K. 2006a Computational analysis of gravitational effects in low-density gas jets. AIAA 44 (7), 1505–1515.Google Scholar
Satti, R. P. & Agrawal, A. K. 2006b Flow structure in the near-field of buoyant low-density gas jets. Intl J. Heat Fluid Flow 27 (2), 336–347.CrossRefGoogle Scholar
Subbarao, E. R. & Cantwell, B. J. 1992 Investigation of a co-flowing buoyant jet: experiments on the effect of Reynolds number and Richardson number. J. Fluid Mech. 245, 69–90.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics. Clarendon.Google Scholar
Tveitereid, M. & Riley, D. S. 1992 Nonparallel flow stability of an axisymmetric buoyant plume in a coflowing uniform stream. Phys. Fluids A 4 (10), 2151–2161.Google Scholar
Wakitani, S. 1980 The stability of a natural convection flow above a point heat source. J. Phys. Soc. Japan 49 (6), 2392–2399.Google Scholar
Worster, M. G. 1986 The axisymmetric laminar plume: asymptotic solution for large Prandtl number. Stud. Appl. Maths 75, 139–152.Google Scholar
Yih, C. S. 1988 Fluid Mechanics. West River Press.Google Scholar