Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T21:04:55.010Z Has data issue: false hasContentIssue false
  • English
  • Français

A local model for the limiting configuration of interfacial solitary waves

Published online by Cambridge University Press:  25 June 2021

X. Guan ,
J.-M. Vanden-Broeck ,
Z. Wang Open the ORCID record for Z. Wang [Opens in a new window]  and
F. Dias Open the ORCID record for F. Dias [Opens in a new window]
X. Guan
Affiliation:
Institute of Mechanics, Chinese Academy of Sciences, Beijing100190, PR China Department of Mathematics, University College London, LondonWC1E 6BT, UK
J.-M. Vanden-Broeck
Affiliation:
Department of Mathematics, University College London, LondonWC1E 6BT, UK
Z. Wang*
Affiliation:
Institute of Mechanics, Chinese Academy of Sciences, Beijing100190, PR China
F. Dias
Affiliation:
School of Mathematics and Statistics, University College Dublin, Belfield, Dublin4, Ireland
*
†Email address for correspondence: zwang@imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

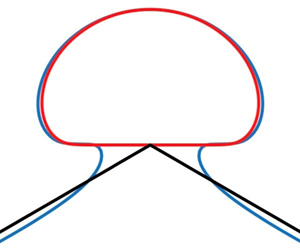
The limiting configuration of interfacial solitary waves between two homogeneous fluids consisting of a sharp $120^{\circ }$ angle with an enclosed bubble of stagnant heavier fluid on top is investigated numerically. We use a boundary integral equation method to compute the almost limiting profiles which are nearly self-intersecting and thus extend the work of Pullin & Grimshaw (Phys. Fluids, vol. 31, 1988, pp. 3550–3559) by obtaining the overhanging solutions for very small density ratios. To further study the local configuration of the limiting profile, we propose a reduced model that replaces the $120^{\circ }$ angle with two straight solid walls intersecting at the bottom of the bubble. Using a series truncation method, a one-parameter family of solutions depending on the angle between the two solid walls (denoted by $\gamma$) is found. When $\gamma = {2{\rm \pi} }/{3}$, it is shown that the simplified model agrees well with the near-limiting wave profile if the density ratio is small, and thus provides a good local approximation to the assumed limiting configuration. Interesting solutions for other values of $\gamma$ are also explored.

JFM classification

Waves/Free-surface Flows: Solitary waves Geophysical and Geological Flows: Internal waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 921 , 25 August 2021 , A9
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Amick, C.J., Fraenkel, L.E. & Toland, J.F. 1982 On the stokes conjecture for the wave of extreme form. Acta Math. 148 (1), 193–214.CrossRefGoogle Scholar
Amick, C.J. & Turner, R.E.L. 1986 A global theory of internal solitary waves in two-fluid systems. Trans. Am. Math. Soc. 298 (2), 431–484.CrossRefGoogle Scholar
Benjamin, T.B. & Bridges, T.J. 1997 Reappraisal of the Kelvin–Helmholtz problem. Part 2. Interaction of the Kelvin–Helmholtz, superharmonic and Benjamin–Feir instabilities. J. Fluid Mech. 333, 327–373.CrossRefGoogle Scholar
Daboussy, D., Dias, F. & Vanden-Broeck, J.-M. 1998 Gravity flows with a free surface of finite extent. Eur. J. Mech. B/Fluids 17, 19–31.CrossRefGoogle Scholar
Funakoshi, M. & Oikawa, M. 1986 Long internal waves of large amplitude in a two-layer fluid. J. Phys. Soc. Japan 55, 128–144.CrossRefGoogle Scholar
Grimshaw, R.H.J. & Pullin, D.I. 1986 Extreme interfacial waves. Phys. Fluids 29 (9), 2802–2807.CrossRefGoogle Scholar
Havelock, T.H. 1918 Periodic irrotational waves of finite height. Proc. R. Soc. A 665, 38–51.Google Scholar
Hunter, J.K. & Vanden-Broeck, J.-M. 1983 Accurate computations for steep solitary waves. J. Fluid Mech. 136, 62–71.CrossRefGoogle Scholar
Kataoka, T. 2006 The stability of finite-amplitude interfacial solitary waves. Fluid Dyn. Res. 38, 831–867.CrossRefGoogle Scholar
Lenau, C.W. 1966 The solitary wave of maximum amplitude. J. Fluid Mech. 26, 309–320.CrossRefGoogle Scholar
Longuet-Higgins, M.S. 1973 On the form of the highest progressive and standing waves in deep water. Proc. R. Soc. A 331, 445–456.Google Scholar
Longuet-Higgins, M.S. & Tanaka, M. 1997 On the crest instabilities of steep surface waves. J. Fluid Mech. 336, 51–68.CrossRefGoogle Scholar
Maklakov, D.V. 2020 A note on the existence of pure gravity waves at the interface of two fluids. Physica D 401, 132157.CrossRefGoogle Scholar
Maklakov, D.V. & Sharipov, R.R. 2018 Almost limiting configurations of steady interfacial overhanging gravity waves. J. Fluid Mech. 856, 673–708.CrossRefGoogle Scholar
Meiron, D.I. & Saffman, P.G. 1983 Overhanging interfacial gravity waves of large amplitude. J. Fluid Mech. 129, 213–218.CrossRefGoogle Scholar
Okamoto, H. & Shoji, M. 2001 The Mathematical Theory of Permanent Progressive Water–waves. Advanced Series in Nonlinear Dynamics, vol. 20. World Scientific.CrossRefGoogle Scholar
Pullin, D.I. & Grimshaw, R.H.J. 1988 Finite-amplitude solitary waves at the interface between two homogeneous fluids. Phys. Fluids 31 (12), 3550–3559.CrossRefGoogle Scholar
Rusås, P.-O. & Grue, J. 2002 Solitary waves and conjugate flows in a three-layer fluid. Eur. J. Mech. B/Fluids 21, 185–206.CrossRefGoogle Scholar
Schwartz, L.W. 1974 Computer extension and analytic continuation of Stokes’ expansion for gravity waves. J. Fluid Mech. 62, 553–578.CrossRefGoogle Scholar
Saffman, P.G. & Yuen, H.C. 1982 Finite-amplitude interfacial waves in the presence of a current. J. Fluid Mech. 123, 459–476.CrossRefGoogle Scholar
Sha, H. & Vanden-Broeck, J.-M. 1993 Two-layer flows past a semicircular obstruction. Phys. Fluids A 5, 2661–2668.CrossRefGoogle Scholar
Taylor, G.I. 1953 An experimental study of standing waves. Proc. R. Soc. A 218, 44–59.Google Scholar
Turner, R.E.L. & Vanden-Broeck, J.-M. 1986 The limiting configuration of interfacial gravity waves. Phys. Fluids 29 (2), 372–375.CrossRefGoogle Scholar
Turner, R.E.L. & Vanden-Broeck, J.-M. 1988 Broadening of interfacial solitary waves. Phys. Fluids 31 (9), 2486–2490.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. & Schwartz, L.W. 1979 Numerical computation of steep gravity waves in shallow water. Phys. Fluids 22 (10), 1868–1871.CrossRefGoogle Scholar
Villermaux, E. & Pomeau, Y. 2010 Super free fall. J. Fluid Mech. 642, 147–157.CrossRefGoogle Scholar
Yamada, H. 1957 a Highest waves of permanent type on the surface of deep water. Rep. Res. Inst. Appl. Mech. Kyushu Univ. 5, 37–52.Google Scholar
Yamada, H. 1957 b On the highest solitary wave. Rep. Res. Inst. Appl. Mech. Kyushu Univ. 5, 53–67.Google Scholar