Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T17:00:12.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Local versus volume-integrated turbulence and mixing in breaking internal waves on slopes

Published online by Cambridge University Press:  17 February 2017

Robert S. Arthur Open the ORCID record for Robert S. Arthur [Opens in a new window] ,
Jeffrey R. Koseff  and
Oliver B. Fringer
Robert S. Arthur*
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Jeffrey R. Koseff
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Oliver B. Fringer
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: barthur@berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Using direct numerical simulations (DNS), we explore local and volume-integrated measures of turbulence and mixing in breaking internal waves on slopes. We consider eight breaking wave cases with a range of normalized pycnocline thicknesses 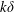$k\unicode[STIX]{x1D6FF}$, where 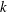$k$ is the horizontal wavenumber and 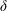$\unicode[STIX]{x1D6FF}$ is the pycnocline thickness, but with similar incoming wave properties. The energetics of wave breaking is quantified in terms of local turbulent dissipation and irreversible mixing using the method of Scotti & White (J. Fluid Mech., vol. 740, 2014, pp. 114–135). Local turbulent mixing efficiencies are calculated using the irreversible flux Richardson number 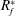$R_{f}^{\ast }$ and are found to be a function of the turbulent Froude number 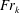$Fr_{k}$. Volume-integrated measures of the turbulent mixing efficiency during wave breaking are also made, and are found to be functions of 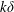$k\unicode[STIX]{x1D6FF}$. The bulk turbulent mixing efficiency ranges from 0.25 to 0.37 and is maximized when 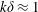$k\unicode[STIX]{x1D6FF}\approx 1$. In order to connect local and bulk mixing efficiency measures, the variation in the bulk turbulent mixing efficiency with 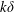$k\unicode[STIX]{x1D6FF}$ is related to the turbulent Froude number at which the maximum total mixing occurs over the course of the breaking event, 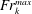$Fr_{k}^{max}$. We find that physically, 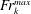$Fr_{k}^{max}$ is controlled by the vertical length scale of billows at the interface during wave breaking.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Topographic effects Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 169 - 198
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aghsaee, P., Boegman, L. & Lamb, K. G. 2010 Breaking of shoaling internal solitary waves. J. Fluid Mech. 659, 289–317.Google Scholar
Arthur, R. S.2015 Numerical investigation of breaking internal waves on slopes: dynamics, energetics, and transport. PhD thesis, Stanford University.Google Scholar
Arthur, R. S. & Fringer, O. B. 2014 The dynamics of breaking internal solitary waves on slopes. J. Fluid Mech. 761, 360–398.Google Scholar
Arthur, R. S. & Fringer, O. B. 2016 Transport by breaking internal gravity waves on slopes. J. Fluid Mech. 789, 93–126.CrossRefGoogle Scholar
Bluteau, C. E., Jones, N. L. & Ivey, G. N. 2013 Turbulent mixing efficiency at an energetic ocean site. J. Geophys. Res. 118 (9), 4662–4672.CrossRefGoogle Scholar
Boegman, L., Ivey, G. N. & Imberger, J. 2005 The degeneration of internal waves in lakes with sloping topography. Limnol. Oceanogr. 50 (5), 1620–1637.Google Scholar
Bogucki, D., Dickey, T. & Redekopp, L. G. 1997 Sediment resuspension and mixing by resonantly generated internal solitary waves. J. Phys. Oceanogr. 27 (7), 1181–1196.Google Scholar
Carter, G. S., Gregg, M. C. & Lien, R. 2005 Internal waves, solitary-like waves, and mixing on the Monterey Bay shelf. Cont. Shelf Res. 25 (12), 1499–1520.Google Scholar
Chou, Y. J. & Fringer, O. B. 2010 A model for the simulation of coupled flow-bed form evolution in turbulent flows. J. Geophys. Res. 115, C10041.CrossRefGoogle Scholar
Cui, A.1999 On the parallel computation of turbulent rotating stratified flows. PhD thesis, Stanford University.Google Scholar
Davis, K. A. & Monismith, S. G. 2011 The modification of bottom boundary layer turbulence and mixing by internal waves shoaling on a barrier reef. J. Phys. Oceanogr. 41 (11), 2223–2241.CrossRefGoogle Scholar
Dörnbrack, A. 1998 Turbulent mixing by breaking gravity waves. J. Fluid Mech. 375, 113–141.CrossRefGoogle Scholar
Dunckley, J. F., Koseff, J. R., Steinbuck, J. V., Monismith, S. G. & Genin, A. 2012 Comparison of mixing efficiency and vertical diffusivity models from temperature microstructure. J. Geophys. Res. 117, C10.Google Scholar
Ferziger, J. H. & Perić, M. 2002 Solution of the Navier–Stokes equations. In Computational Methods for Fluid Dynamics, pp. 157–216. Springer.Google Scholar
Fringer, O. B. & Street, R. L. 2003 The dynamics of breaking progressive interfacial waves. J. Fluid Mech. 494, 319–353.CrossRefGoogle Scholar
Gargett, A. E. & Moum, J. N. 1995 Mixing efficiencies in turbulent tidal fronts: results from direct and indirect measurements of density flux. J. Phys. Oceanogr. 25 (11), 2583–2608.Google Scholar
Härtel, C., Carlsson, F. & Thunblom, M. 2000 Analysis and direct numerical simulation of the flow at a gravity-current head. Part 2. The lobe-and-cleft instability. J. Fluid Mech. 418, 213–229.CrossRefGoogle Scholar
Hosegood, P., Bonnin, J. & van Haren, H. 2004 Solibore-induced sediment resuspension in the Faeroe-Shetland channel. Geophys. Res. Lett. 31, L09301.Google Scholar
Hosegood, P. & van Haren, H. 2004 Near-bed solibores over the continental slope in the Faeroe-Shetland channel. Deep-Sea Res. II 51 (25), 2943–2971.Google Scholar
Hult, E. L., Troy, C. D. & Koseff, J. R. 2011 The mixing efficiency of interfacial waves breaking at a ridge: 2. Local mixing processes. J. Geophys. Res. 116, C02004.Google Scholar
Ivey, G. N. & Imberger, J. 1991 On the nature of turbulence in a stratified fluid. Part i: the energetics of mixing. J. Phys. Oceanogr. 21 (5), 650–658.2.0.CO;2>CrossRefGoogle Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169–184.Google Scholar
Klymak, J. M. & Moum, J. N. 2003 Internal solitary waves of elevation advancing on a shoaling shelf. Geophys. Res. Lett. 30 (20), 2045.Google Scholar
Lamb, K. G. 2002 A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 451, 109–144.Google Scholar
Lamb, K. G. 2014 Internal wave breaking and dissipation mechanisms on the continental slope/shelf. Annu. Rev. Fluid Mech. 46, 231–254.Google Scholar
Leichter, J. J., Wing, S. R., Miller, S. L. & Denny, M. W. 1996 Pulsed delivery of subthermocline water to Conch Reef (Florida Keys) by internal tidal bores. Limnol. Oceanogr. 41 (7), 1490–1501.CrossRefGoogle Scholar
Leonard, B. P. 1979 A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Mech. Engng 19 (1), 59–98.Google Scholar
Lin, C. L., Ferziger, J. H., Koseff, J. R. & Monismith, S. G. 1993 Simulation and stability of two-dimensional internal gravity waves in a stratified shear flow. Dyn. Atmos. Oceans 19 (1), 325–366.Google Scholar
Linden, P. F. & Redondo, J. M. 1991 Molecular mixing in Rayleigh–Taylor instability. Part i: global mixing. Phys. Fluids A 3 (5), 1269–1277.CrossRefGoogle Scholar
Lozovatsky, I. D. & Fernando, H. J. S. 2013 Mixing efficiency in natural flows. Phil. Trans. R. Soc. Lond. A 371, 20120213.Google ScholarPubMed
Mater, B. D. & Venayagamoorthy, S. K. 2014 The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 41 (13), 4646–4653.Google Scholar
McEwan, A. D. 1983a Internal mixing in stratified fluids. J. Fluid Mech. 128, 59–80.Google Scholar
McEwan, A. D. 1983b The kinematics of stratified mixing through internal wave breaking. J. Fluid Mech. 128, 47–57.Google Scholar
Michallet, H. & Ivey, G. N. 1999 Experiments on mixing due to internal solitary waves breaking on uniform slopes. J. Geophys. Res. 104 (C6), 13467–13477.Google Scholar
Moore, C. D., Koseff, J. R. & Hult, E. L. 2016 Characteristics of bolus formation and propagation from breaking internal waves on shelf slopes. J. Fluid Mech. 791, 260–283.Google Scholar
Moum, J. N. 1996 Efficiency of mixing in the main thermocline. J. Geophys. Res. 101 (C5), 12057–12069.CrossRefGoogle Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes ii: energetics of tidal and wind mixing. Deep-Sea Res. 45 (12), 1977–2010.Google Scholar
Oakey, N. S. 1982 Determination of the rate of dissipation of turbulent energy from simultaneous temperature and velocity shear microstructure measurements. J. Phys. Oceanogr. 12 (3), 256–271.Google Scholar
Omand, M. M., Leichter, J. J., Franks, P. J., Guza, R. T., Lucas, A. J. & Feddersen, F. 2011 Physical and biological processes underlying the sudden appearance of a red-tide surface patch in the nearshore. Limnol. Oceanogr. 56 (3), 787–801.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10 (1), 83–89.Google Scholar
Osborn, T. R. & Cox, C. S. 1972 Oceanic fine structure. Geophys. Fluid Dyn. 3 (1), 321–345.CrossRefGoogle Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.CrossRefGoogle Scholar
Pineda, J. 1994 Internal tidal bores in the nearshore: warm-water fronts, seaward gravity currents and the onshore transport of neustonic larvae. J. Mar. Res. 52 (3), 427–458.Google Scholar
Quaresma, L. S., Vitorino, J., Oliveira, A. & da Silva, J. 2007 Evidence of sediment resuspension by nonlinear internal waves on the western Portuguese mid-shelf. Mar. Geol. 246 (2), 123–143.Google Scholar
Rehmann, C. R. & Koseff, J. R. 2004 Mean potential energy change in stratified grid turbulence. Dyn. Atmos. Oceans 37 (4), 271–294.Google Scholar
Scotti, A. & White, B. 2014 Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy. J. Fluid Mech. 740, 114–135.Google Scholar
Seim, H. E. & Gregg, M. C. 1995 Energetics of a naturally occurring shear instability. J. Geophys. Res. 100 (C3), 4943–4958.CrossRefGoogle Scholar
Shih, L. H.2003 Numerical simulations of stably stratified turbulent flow. PhD thesis, Stanford University.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Simpson, J. E. 1972 Effects of the lower boundary on the head of a gravity current. J. Fluid Mech. 53 (4), 759–768.Google Scholar
Slinn, D. N. & Riley, J. J. 1998 Turbulent dynamics of a critically reflecting internal gravity wave. Theor. Comput. Fluid Dyn. 11 (3–4), 281–303.Google Scholar
Smyth, W. D., Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31 (8), 1969–1992.Google Scholar
Troy, C. D. & Koseff, J. R. 2005 The instability and breaking of long internal waves. J. Fluid Mech. 543, 107–136.Google Scholar
Venayagamoorthy, S. K. & Fringer, O. B. 2007 On the formation and propagation of nonlinear internal boluses across a shelf break. J. Fluid Mech. 577, 137–159.CrossRefGoogle Scholar
Venayagamoorthy, S. K. & Koseff, J. R. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1.Google Scholar
Walter, R. K., Squibb, M. E., Woodson, C. B., Koseff, J. R. & Monismith, S. G. 2014a Stratified turbulence in the nearshore coastal ocean: dynamics and evolution in the presence of internal bores. J. Geophys. Res. 119 (12), 8709–8730.CrossRefGoogle Scholar
Walter, R. K., Woodson, C. B., Arthur, R. S., Fringer, O. B. & Monismith, S. G. 2012 Nearshore internal bores and turbulent mixing in southern Monterey Bay. J. Geophys. Res. 117, C07017.Google Scholar
Walter, R. K., Woodson, C. B., Leary, P. R. & Monismith, S. G. 2014b Connecting wind-driven upwelling and offshore stratification to nearshore internal bores and oxygen variability. J. Geophys. Res. 116 (6), 3517–3534.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Yamazaki, H. & Osborn, T. R. 1993 Direct estimation of heat flux in a seasonal thermocline. J. Phys. Oceanogr. 23 (3), 503–516.Google Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33.Google Scholar