Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-14T05:42:50.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Lock-exchange gravity currents propagating in a channel containing an array of obstacles

Published online by Cambridge University Press:  26 January 2015

Ayse Yuksel Ozan ,
George Constantinescu  and
Andrew J. Hogg
Ayse Yuksel Ozan
Affiliation:
Department of Civil and Environmental Engineering, The University of Iowa, Iowa City, IA 52242, USA Department of Civil Engineering, Adnan Menderes University, Main Campus 09100 Aydin, Turkey
George Constantinescu*
Affiliation:
Department of Civil and Environmental Engineering, The University of Iowa, Iowa City, IA 52242, USA
Andrew J. Hogg
Affiliation:
Centre for Environmental and Geophysical Flows, School of Mathematics, University of Bristol, Bristol BS8 1TW, UK
*
†Email address for correspondence: sconstan@engineering.uiowa.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Large eddy simulation (LES) is used to investigate the evolution of Boussinesq gravity currents propagating through a channel of height 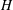$H$ containing a staggered array of identical cylinders of square cross-section and edge length 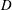$D$. The cylinders are positioned with their axes horizontal and perpendicular to the (streamwise) direction along which the lock-exchange flow develops. The effects of the volume fraction of solids, 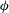${\it\phi}$, the Reynolds number and geometrical parameters describing the array of obstacles on the structure of the lock-exchange flow, total drag force acting on the gravity current, front velocity and global energy budget are analysed. Simulation results show that the currents rapidly transition to a state in which the extra resistance provided by the cylinders strongly retards the motion and dominates the dissipative processes. A shallow layer model is also formulated and similarity solutions for the motion are found in the regime where the driving buoyancy forces are balanced by the drag arising from the interaction with the cylinders. The numerical simulations and this shallow layer model show that low-Reynolds-number currents transition to a drag-dominated regime in which the resistance is linearly proportional to the flow speed and, consequently, the front velocity, 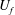$U_{f}$, is proportional to 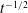$t^{-1/2}$, where $t$ is the time measured starting at the gate release time. By contrast, high-Reynolds-number currents, for which the cylinder Reynolds number is sufficiently high that the drag coefficient for most of the cylinders can be considered constant, transition first to a quadratic drag-dominated regime in which the front speed determined from the simulations is given by 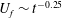$U_{f}\sim t^{-0.25}$, before undergoing a subsequent transition to the aforementioned linear drag regime in which 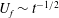$U_{f}\sim t^{-1/2}$. Meanwhile, away from the front, the depth-averaged gravity current velocity is proportional to 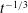$t^{-1/3}$, a result that is in agreement with the shallow water model. It is suggested that the difference between these two is due to mixing processes, which are shown to be significant in the numerical simulations, especially close to the front of the motion. Direct estimation of the drag coefficient 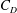$C_{D}$ from the numerical simulations shows that the combined drag parameter for the porous medium, 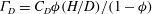${\it\Gamma}_{D}=C_{D}{\it\phi}(H/D)/(1-{\it\phi})$, is the key dimensionless grouping of variables that determines the speed of propagation of the current within arrays with different $C_{D},{\it\phi}$ and 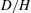$D/H$.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 544 - 575
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cantero, M. I., Lee, J. R., Balachandar, S. & Garcia, M. H. 2007 On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.Google Scholar
Chang, K. S. & Constantinescu, G. 2013 Coherent structures in developing flow over 2D dunes. Water Resour. Res. 49, 2466–2460.Google Scholar
Chang, K. S., Constantinescu, G. & Park, S. O. 2006 Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J. Fluid Mech. 561, 113–145.Google Scholar
Chang, K. S., Constantinescu, G. & Park, S. O. 2007 The purging of a neutrally buoyant or a dense miscible contaminant from a rectangular cavity. Part II: the case of an incoming fully turbulent overflow. ASCE J. Hydraul. Engng 133 (4), 373–385.CrossRefGoogle Scholar
Chimney, M. J., Wenkert, L. & Pietro, K. C. 2006 Patterns of vertical stratification in a subtropical constructed wetland in south Florida (USA). Ecol. Engng 27, 322–330.CrossRefGoogle Scholar
Coates, M. & Ferris, J. 1994 The radiatively-driven natural convection beneath a floating plant layer. Limnol. Oceanogr. 39 (5), 1186–1194.Google Scholar
Constantinescu, G. 2014 LES of lock-exchange compositional gravity currents: a brief review of some recent results. Environ. Fluid Mech. 14, 295–317.Google Scholar
Edwards, A. M., Wright, D. G. & Platt, T. 2004 Biological heating effects of a band of phytoplankton. J. Mar. Syst. 49, 89–103.CrossRefGoogle Scholar
Ermanyuk, E. V. & Gavrilov, N. V. 2005a Interaction of an internal gravity current with a submerged circular cylinder. J. Appl. Mech. Tech. Phys. 46 (2), 216–223.Google Scholar
Ermanyuk, E. V. & Gavrilov, N. V. 2005b Interaction of an internal gravity current with an obstacle on the channel bottom. J. Appl. Mech. Tech. Phys. 46 (4), 489–495.Google Scholar
Furukawa, K., Wolanski, E. & Mueller, H. 1997 Currents and sediment transport in mangrove forests. Eastuar. Coast. Shelf Sci. 44, 301–310.Google Scholar
Gonzalez-Juez, E., Meiburg, E. & Constantinescu, G. 2009 Gravity currents impinging on bottom mounted square cylinders: flow fields and associated forces. J. Fluid Mech. 631, 65–102.CrossRefGoogle Scholar
Gonzalez-Juez, E., Meiburg, E., Tokyay, T. & Constantinescu, G. 2010 Gravity current flow past a circular cylinder: forces and wall shear stresses and implications for scour. J. Fluid Mech. 649, 69–102.Google Scholar
Hákonardóttir, K. M., Hogg, A. J., Jóhannesson, T., Kern, M. & Tiefenbacher, F. 2003 Large-scale avalanche breaking mounds and catching dam experiments with snow: a study of the airborne jet. Surv. Geophys. 24, 543–554.CrossRefGoogle Scholar
Härtel, C., Meiburg, E. & Necker, F. 2000 Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries. J. Fluid Mech. 418, 189–212.Google Scholar
Hatcher, L., Hogg, A. J. & Woods, A. W. 2000 The effects of drag on turbulent gravity currents. J. Fluid Mech. 416, 297–314.CrossRefGoogle Scholar
Hogg, A. J. 2006 Lock-release gravity currents and dam-break flows. J. Fluid Mech. 569, 61–87.Google Scholar
Hopfinger, E. J. 1983 Snow avalanche motion and related phenomena. Annu. Rev. Fluid Mech. 15, 47–76.CrossRefGoogle Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.Google Scholar
Huppert, H. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.Google Scholar
Huppert, H. & Woods, A. W. 1995 Gravity-current flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Jamali, M., Zhang, X. & Nepf, H. 2008 Exchange flow between a canopy and open water. J. Fluid Mech. 611, 237–254.Google Scholar
Keulegan, G. H. 1957 An experimental study of the motion of saline water from locks into fresh water channels. US Natl. Bur. Stand. Rep. 5168.Google Scholar
King, A. T., Tinoco, R. O. & Cowen, E. A. 2012 A ${\it\kappa}{-}{\it\varepsilon}$ turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 701, 1–39.Google Scholar
Kirkpatrick, M. P., Ackerman, A. S., Stevens, D. & Mansour, N. N. 2006 On the application of the dynamic Smagorinsky model to large eddy simulations of the cloud-topped atmospheric boundary layer. J. Atmos. Sci. 63, 526–546.Google Scholar
Leonard, B. P. 1979 A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Mech. Engng 19, 59–98.CrossRefGoogle Scholar
Lindsey, W. F.1987 Drag of cylinders of simple shape, National Advisory Committee for Aeronautics. NACA Report 619, Langley Field, VA.Google Scholar
Meiburg, E. & Kneller, B. 2010 Turbidity currents and their deposits. Annu. Rev. Fluid Mech. 42, 135–156.Google Scholar
Naaim-Bouvet, F., Naaim, M., Bacher, M. & Heiligenstein, L. 2002 Physical modelling of the interaction between powder avalanches and defence structures. Nat. Hazards Earth Syst. Sci. 2, 193–202.Google Scholar
Necker, F., Härtel, C., Kleiser, L. & Meiburg, E. 2002 High-resolution simulations of particle-driven gravity currents. Intl J. Multiphase Flow 28, 279–300.Google Scholar
Necker, F., Härtel, C., Kleiser, L. & Meiburg, E. 2005 Mixing and dissipation in particle-driven gravity currents. J. Fluid Mech. 545, 339–372.CrossRefGoogle Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Oehy, C. D. & Schleiss, A. J. 2007 Control of turbidity currents in reservoirs by solid and permeable obstacles. J. Hydraul. Engng 133 (6), 637–648.Google Scholar
Ooi, S. K., Constantinescu, S. G. & Weber, L. 2007 A numerical study of intrusive compositional gravity currents. Phys. Fluids 19, 076602.CrossRefGoogle Scholar
Ooi, S. K., Constantinescu, S. G. & Weber, L. 2009 Numerical simulations of lock exchange compositional gravity currents. J. Fluid Mech. 635, 361–388.Google Scholar
Pierce, C. D. & Moin, P.2001 Progress-variable approach for large-eddy simulation of turbulent combustion. Mech. Eng. Dept. Rep. TF-80. Stanford University, California, USA.Google Scholar
Pierce, C. D. & Moin, P. 2004 Progress-variable approach for large-eddy simulation of nonpremixed turbulent combustion. J. Fluid Mech. 504, 73–97.CrossRefGoogle Scholar
Rodi, W., Constantinescu, G. & Stoesser, T. 2013 Large Eddy Simulation in Hydraulics. (IAHR Monograph) , CRC Press, Taylor & Francis Group, ISBN-10: 1138000247.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.CrossRefGoogle Scholar
Shin, J., Dalziel, S. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.Google Scholar
Tanino, Y., Nepf, H. M. & Kulis, P. S. 2005 Gravity currents in aquatic canopies. Water Resour. Res. 41, W12402.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2011 Lock exchange gravity currents with a high volume of release propagating over an array of obstacles. J. Fluid Mech. 672, 570–605.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2012 Tail structure and bed friction velocity distribution of gravity currents propagating over an array of obstacles. J. Fluid Mech. 694, 252–291.CrossRefGoogle Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2014 Lock exchange gravity currents with a low volume of release propagating over an array of obstacles. J. Geophys. Res. Oceans 119, 2752–2768.CrossRefGoogle Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. CRC Press, Taylor & Francis Group, LLC, ISBN 978-1-58488-903-8.CrossRefGoogle Scholar
Yoon, D. H., Yang, K. S. & Choi, C. B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22, 043603.Google Scholar
Zhang, X. & Nepf, H. 2008 Density-driven exchange flow between open water and an aquatic canopy. Water Resour. Res. 44, W08417.CrossRefGoogle Scholar
Zhang, X. & Nepf, H. 2011 Exchange flow between open water and floating vegetation. Environ. Fluid Mech. 11 (5), 531–546.Google Scholar