Article contents
Longitudinal–transverse aerodynamic force in viscous compressible complex flow
Published online by Cambridge University Press: 01 September 2014
Abstract
We report our systematic development of a general and exact theory for diagnosis of total force and moment exerted on a generic body moving and deforming in a calorically perfect gas. The total force and moment consist of a longitudinal part (L-force) due to compressibility and irreversible thermodynamics, and a transverse part (T-force) due to shearing. The latter exists in incompressible flow but is now modulated by the former. The theory represents a full extension of a unified incompressible diagnosis theory of the same type developed by J. Z. Wu and coworkers to compressible flow, with Mach number ranging from low-subsonic to moderate-supersonic flows. Combined with computational fluid dynamics (CFD) simulation, the theory permits quantitative identification of various complex flow structures and processes responsible for the forces, and thereby enables rational optimal configuration design and flow control. The theory is confirmed by a numerical simulation of circular-cylinder flow in the range of free-stream Mach number 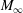 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M_{\infty }$ between 0.2 and 2.0. The L-drag and T-drag of the cylinder vary with
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M_{\infty }$ between 0.2 and 2.0. The L-drag and T-drag of the cylinder vary with 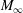 $M_{\infty }$ in different ways, the underlying physical mechanisms of which are analysed. Moreover, each L-force and T-force integrand contains a universal factor of local Mach number
$M_{\infty }$ in different ways, the underlying physical mechanisms of which are analysed. Moreover, each L-force and T-force integrand contains a universal factor of local Mach number 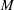 $M$. Our preliminary tests suggest that the possibility of finding new similarity rules for each force constituent could be quite promising.
$M$. Our preliminary tests suggest that the possibility of finding new similarity rules for each force constituent could be quite promising.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 27
- Cited by


