Article contents
A macrotransport equation for the particle distribution in the flow of a concentrated, non-colloidal suspension through a circular tube
Published online by Cambridge University Press: 08 October 2013
Abstract
A two-time-scale perturbation expansion is used to derive a cross-section-averaged convection–dispersion equation for the particle distribution in the flow of a concentrated suspension of neutrally buoyant, non-colloidal particles through a straight, circular tube. Since the cross-streamline motion of particles is governed by shear-induced migration, the Taylor-dispersion coefficient 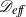 ${\mathscr{D}}_{eff} $ scales as
${\mathscr{D}}_{eff} $ scales as 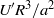 ${U}^{\prime } {R}^{3} / {a}^{2} $,
${U}^{\prime } {R}^{3} / {a}^{2} $, 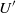 ${U}^{\prime } $,
${U}^{\prime } $, 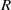 $R$ and
$R$ and  $a$ being the characteristic velocity scale, the tube radius and the particle radius, respectively. Here
$a$ being the characteristic velocity scale, the tube radius and the particle radius, respectively. Here  ${\mathscr{D}}_{eff} $ is found to decrease monotonically with an increase in the particle concentration. The linear dependence of
${\mathscr{D}}_{eff} $ is found to decrease monotonically with an increase in the particle concentration. The linear dependence of 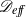 ${\mathscr{D}}_{eff} $ on
${\mathscr{D}}_{eff} $ on 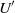 ${U}^{\prime } $ implies that changes in the cross-section averaged axial concentration profile are dependent only on the total axial strain experienced by the suspension. This stipulates that the spatial evolution of a fluctuation in the concentration of particles in the flowing suspension, or the width of the mixing zone between two regions of different concentrations in the tube will be independent of the suspension velocity in the tube. A second interesting feature in particulate dispersion is that the effective velocity of the particulate phase is concentration-dependent, which, by itself (i.e. without considering Taylor dispersion), can produce either sharpening or relaxation of concentration gradients. In particular, shocks with positive concentration gradients along the flow direction can asymptotically evolve into time-independent distributions in an appropriately chosen frame of reference, and concentration pulses relax asymmetrically. These trends are contrasted with those expected from the classical problem of Taylor dispersion of a passive tracer in the same geometry. The results in this paper are especially relevant for suspension flows through microfluidic geometries, where the induction lengths for shear-induced migration are short.
${U}^{\prime } $ implies that changes in the cross-section averaged axial concentration profile are dependent only on the total axial strain experienced by the suspension. This stipulates that the spatial evolution of a fluctuation in the concentration of particles in the flowing suspension, or the width of the mixing zone between two regions of different concentrations in the tube will be independent of the suspension velocity in the tube. A second interesting feature in particulate dispersion is that the effective velocity of the particulate phase is concentration-dependent, which, by itself (i.e. without considering Taylor dispersion), can produce either sharpening or relaxation of concentration gradients. In particular, shocks with positive concentration gradients along the flow direction can asymptotically evolve into time-independent distributions in an appropriately chosen frame of reference, and concentration pulses relax asymmetrically. These trends are contrasted with those expected from the classical problem of Taylor dispersion of a passive tracer in the same geometry. The results in this paper are especially relevant for suspension flows through microfluidic geometries, where the induction lengths for shear-induced migration are short.
JFM classification
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 14
- Cited by


