Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T07:54:40.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Markovian inhomogeneous closures for Rossby waves and turbulence over topography

Published online by Cambridge University Press:  31 October 2018

Jorgen S. Frederiksen Open the ORCID record for Jorgen S. Frederiksen [Opens in a new window]  and
Terence J. O’Kane
Jorgen S. Frederiksen*
Affiliation:
CSIRO Oceans and Atmosphere, Aspendale, Victoria, 3195, and Hobart, Tasmania, 7004, Australia
Terence J. O’Kane
Affiliation:
CSIRO Oceans and Atmosphere, Aspendale, Victoria, 3195, and Hobart, Tasmania, 7004, Australia
*
†Email address for correspondence: Jorgen.Frederiksen@csiro.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Manifestly Markovian closures for the interaction of two-dimensional inhomogeneous turbulent flows with Rossby waves and topography are formulated and compared with large ensembles of direct numerical simulations (DNS) on a generalized 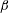$\unicode[STIX]{x1D6FD}$-plane. Three versions of the Markovian inhomogeneous closure (MIC) are established from the quasi-diagonal direct interaction approximation (QDIA) theory by modifying the response function to a Markovian form and employing respectively the current-time (quasi-stationary) fluctuation dissipation theorem (FDT), the prior-time (non-stationary) FDT and the correlation FDT. Markov equations for the triad relaxation functions are derived that carry similar information to the time-history integrals of the non-Markovian QDIA closure but become relatively more efficient for long integrations. Far from equilibrium processes are studied, where the impact of a westerly mean flow on a conical mountain generates large-amplitude Rossby waves in a turbulent environment, over a period of 10 days. Excellent agreement between the evolved mean streamfunction and mean and transient kinetic energy spectra are found for the three versions of the MIC and two variants of the non-Markovian QDIA compared with an ensemble of 1800 DNS. In all cases mean Rossby wavetrain pattern correlations between the closures and the DNS ensemble are greater than 0.9998.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Turbulent Flows: Turbulence theory Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 45 - 70
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bowman, J. C., Krommes, J. A. & Ottaviani, M. 1993 The realizable Markovian closure. Part I. General theory, with application to three-wave dynamics. Phys. Fluids B 5, 3558–3589.Google Scholar
Bowman, J. C. & Krommes, J. A. 1997 The realizable Markovian closure and realizable test-field model. Part II. Application to anisotropic drift-wave dynamics. Phys. Plasmas 4, 3895–3909.Google Scholar
Cambon, C., Mons, V., Gréa, B.-J. & Rubinstein, R. 2017 Anisotropic triadic closures for shear-driven and buoyancy-driven turbulent flows. Comput. Fluids 151, 73–84.Google Scholar
Carnevale, G. F. & Frederiksen, J. S. 1983a Viscosity renormalization based on direct-interaction closure. J. Fluid Mech. 131, 289–304.Google Scholar
Carnevale, G. F. & Frederiksen, J. S. 1983b A statistical dynamical theory of strongly nonlinear internal gravity waves. Geophys. Astrophys. Fluid Dyn. 23, 175–207.Google Scholar
Carnevale, G. F. & Frederiksen, J. S. 1987 Nonlinear stability and statistical mechanics of flow over topography. J. Fluid Mech. 175, 157–181.Google Scholar
Carnevale, G. F., Frisch, U. & Salmon, R. 1981 H theorems in statistical fluid dynamics. J. Phys. A: Math. Gen. 14, 1701–1718.Google Scholar
Carnevale, G. F. & Martin, P. C. 1982 Field theoretic techniques in statistical fluid dynamics: with application to nonlinear wave dynamics. Geophys. Astrophys. Fluid Dyn. 20, 131–164.Google Scholar
Deker, U. & Haake, F. 1975 Fluctuation–dissipation theorems for classical processes. Phys. Rev. A 11, 2043–2056.Google Scholar
Epstein, E. S. 1969a The role of initial uncertainties in prediction. J. Appl. Meteorol. 8, 190–198.Google Scholar
Epstein, E. S. 1969b Stochastic dynamic prediction. Tellus 21, 739–759.Google Scholar
Epstein, E. S. & Pitcher, E. J. 1972 Stochastic analysis of meteorological fields. J. Atmos. Sci. 29, 244–257.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2007 Structure and spacing of jets in barotropic turbulence. J. Atmos. Sci. 64, 3652–3665.Google Scholar
Fleming, R. J. 1971a On stochastic dynamic prediction. Part I. The energetics of uncertainty and the question of closure. Mon. Weath. Rev. 99, 851–872.Google Scholar
Fleming, R. J. 1971b On stochastic dynamic prediction. Part II. Predictability and utility. Mon. Weath. Rev. 99, 927–938.Google Scholar
Frederiksen, J. S. 1982 Eastward and westward flows over topography in nonlinear and linear barotropic models. J. Atmos. Sci. 39, 2477–2489.Google Scholar
Frederiksen, J. S. 1999 Subgrid-scale parameterizations of eddy–topographic force, eddy viscosity and stochastic backscatter for flow over topography. J. Atmos. Sci. 56, 1481–1494.Google Scholar
Frederiksen, J. S. 2003 Renormalized closure theory and subgrid-scale parameterizations for two-dimensional turbulence. In Nonlinear Dynamics: From Lasers to Butterflies (ed. Ball, R. & Akhmediev, N.), Lecture Notes in Complex Systems, vol. 1, chap. 6, pp. 225–256. World Scientific.Google Scholar
Frederiksen, J. S. 2012a Statistical dynamical closures and subgrid modeling for QG and 3D inhomogeneous turbulence. Entropy 14, 32–57.Google Scholar
Frederiksen, J. S. 2012b Self-energy closure for inhomogeneous turbulent flows and subgrid modeling. Entropy 14, 769–799.Google Scholar
Frederiksen, J. S. 2017 Quasi-diagonal inhomogeneous closure for classical and quantum statistical dynamics. J. Math. Phys. 58, 103303.Google Scholar
Frederiksen, J. S. & Davies, A. G. 1997 Eddy viscosity and stochastic backscatter parameterizations on the sphere for atmospheric circulation models. J. Atmos. Sci. 54, 2475–2492.Google Scholar
Frederiksen, J. S & Davies, A. G. 2000 Dynamics and spectra of cumulant update closures for two-dimensional turbulence. Geophys. Astrophys. Fluid Dyn. 92, 197–231.Google Scholar
Frederiksen, J. S. & Davies, A. G. 2004 The regularized DIA closure for two-dimensional turbulence. Geophys. Astrophys. Fluid Dyn. 98, 203–223.Google Scholar
Frederiksen, J. S., Davies, A. G. & Bell, R. C. 1994 Closure theories with non-Gaussian restarts for truncated two-dimensional turbulence. Phys. Fluids 6, 3153–3163.Google Scholar
Frederiksen, J. S., Dix, M. R. & Kepert, S. M. 1996 Systematic energy errors and the tendency towards canonical equilibrium in atmospheric circulation models. J. Atmos. Sci. 53, 887–904.Google Scholar
Frederiksen, J. S., Kitsios, V., O’Kane, T. J. & Zidikheri, M. J. 2017 Stochastic subgrid modelling for geophysical and three-dimensional turbulence. In Nonlinear and Stochastic Climate Dynamics (ed. Franzke, C. J. E. & O’Kane, T. J.), pp. 241–275. Cambridge University Press.Google Scholar
Frederiksen, J. S. & O’Kane, T. J. 2005 Inhomogeneous closure and statistical mechanics for Rossby wave turbulence over topography. J. Fluid Mech. 539, 137–165.Google Scholar
Frederiksen, J. S. & O’Kane, T. J. 2008 Entropy, closures and subgrid modeling. Entropy 10, 635–683.Google Scholar
Gotoh, T., Kaneda, Y. & Bekki, N. 1988 Numerical integration of the Lagrangian renormalized approximation. J. Phys. Soc. Japan 57, 866–880.Google Scholar
Hasselmann, K. 1966 Feynman diagrams and interaction rules of wave–wave scattering processes. Rev. Geophys. 4, 1–32.Google Scholar
Herring, J. R. 1965 Self-consistent-field approach to turbulence theory. Phys. Fluids 8, 2219–2225.Google Scholar
Herring, J. R. 1966 Self-consistent-field approach to nonstationary turbulence. Phys. Fluids 9, 2106–2110.Google Scholar
Herring, J. R. 1977 Two-dimensional topographic turbulence. J. Atmos. Sci. 34, 1731–1750.Google Scholar
Herring, J. R. & Kraichnan, R. H. 1979 A numerical comparison of velocity-based and strain-based Lagrangian-history turbulence approximations. J. Fluid Mech. 91, 581–597.Google Scholar
Herring, J. R., Orszag, S. A., Kraichnan, R. H. & Fox, D. G. 1974 Decay of two-dimensional homogeneous turbulence. J. Fluid Mech. 66, 417–444.Google Scholar
Holloway, G. 1978 A spectral theory of nonlinear barotropic motion above irregular topography. J. Phys. Oceanogr. 8, 414–427.Google Scholar
Hu, G., Krommes, J. A. & Bowman, J. C. 1997 Statistical theory of resistive drift-wave turbulence and transport. Phys. Plasmas 4, 2116–2133.Google Scholar
Kaneda, Y. 1981 Renormalised expansions in the theory of turbulence with the use of the Lagrangian position function. J. Fluid Mech. 107, 131–145.Google Scholar
Kasahara, A. 1966 The dynamical influence of orography on the large scale motion of the atmosphere. J. Atmos. Sci. 23, 259–270.Google Scholar
Kiyani, K. & McComb, W. D. 2004 Time-ordered fluctuation–dissipation relation for incompressible isotropic turbulence. Phys. Rev. E 70, 066303.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very high Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kraichnan, R. H. 1959a The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.Google Scholar
Kraichnan, R. H. 1959b Classical fluctuation–relaxation theorem. Phys. Rev. 113, 1181–1182.Google Scholar
Kraichnan, R. H. 1964a Decay of isotropic turbulence in the direct-interaction approximation. Phys. Fluids 7, 1030–1048.Google Scholar
Kraichnan, R. H. 1964b Direct-interaction approximation for shear and thermally driven turbulence. Phys. Fluids 7, 1048–1082.Google Scholar
Kraichnan, R. H. 1964c Kolmogorov’s hypothesis and Eulerian turbulence theory. Phys. Fluids 7, 1723–1733.Google Scholar
Kraichnan, R. H. 1965 Lagrangian-history approximation for turbulence. Phys. Fluids 8, 575–598.Google Scholar
Kraichnan, R. H. 1971 An almost-Markovian Galilean-invariant turbulence model. J. Fluid Mech. 47, 513–524.Google Scholar
Kraichnan, R. H. 1972 Test-field model for inhomogeneous turbulence. J. Fluid Mech. 56, 287–304.Google Scholar
Kraichnan, R. H. 1977 Eulerian and Lagrangian renormalization in turbulence theory. J. Fluid Mech. 83, 349–374.Google Scholar
Kraichnan, R. H. & Herring, J. R. 1978 A strain-based Lagrangian-history turbulence theory. J. Fluid Mech. 88, 355–367.Google Scholar
Krommes, J. A. 2002 Fundamental descriptions of plasma turbulence in magnetic fields. Phys. Rep. 360, 1–352.Google Scholar
Leith, C. E. 1971 Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 28, 145–161.Google Scholar
Leith, C. E. & Kraichnan, R. H. 1972 Predictability of turbulent flows. J. Atmos. Sci. 29, 1041–1058.Google Scholar
Martin, P. C., Siggia, E. D. & Rose, H. A. 1973 Statistical dynamics of classical systems. Phys. Rev. A 8, 423–437.Google Scholar
Marston, J. B., Qi, W. & Tobias, S. M.2016 Direct statistical simulation of a jet. arXiv:1412.0381v2.Google Scholar
McComb, W. D. 1974 A local energy-transfer theory of isotropic turbulence. J. Phys. A 7, 632–649.Google Scholar
McComb, W. D. 1990 The Physics of Fluid Turbulence. Oxford University Press.Google Scholar
McComb, W. D. 2004 Renormalization Methods. Oxford University Press.Google Scholar
McComb, W. D. 2014 Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press.Google Scholar
Millionshtchikov, M. 1941 On the theory of homogeneous isotropic turbulence. Dokl. Akad. Nauk. SSSR 32, 615–618.Google Scholar
Newell, A. C. & Rumpf, B. 2011 Wave turbulence. Annu. Rev. Fluid Mech. 43, 59–78.Google Scholar
Ogura, Y. 1963 A consequence of the zero fourth order cumulant approximation in the decay of isotropic turbulence. J. Fluid Mech. 16, 33–40.Google Scholar
O’Kane, T. J. & Frederiksen, J. S. 2004 The QDIA and regularized QDIA closures for inhomogeneous turbulence over topography. J. Fluid Mech. 65, 133–165.Google Scholar
O’Kane, T. J. & Frederiksen, J. S. 2008a A comparison of statistical dynamical and ensemble prediction methods during blocking. J. Atmos. Sci. 65, 426–447.Google Scholar
O’Kane, T. J. & Frederiksen, J. S. 2008b Comparison of statistical dynamical, square root and ensemble Kalman filters. Entropy 10, 684–721.Google Scholar
O’Kane, T. J. & Frederiksen, J. S. 2008c Statistical dynamical subgrid-scale parameterizations for geophysical flows. Phys. Scr. T142, 014042.Google Scholar
O’Kane, T. J. & Frederiksen, J. S. 2010 Application of statistical dynamical closures to data assimilation. Phys. Scr. T132, 014033.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Pitcher, E. J. 1977 Application of stochastic dynamic prediction to real data. J. Atmos. Sci. 34, 3–21.Google Scholar
Rose, H. A. 1985 An efficient non-Markovian theory of non-equilibrium dynamics. Physica D 14, 216–226.Google Scholar
Srinivasan, K. & Young, W. R. 2012 Zonostropic instability. J. Atmos. Sci. 69, 1633–1656.Google Scholar
Yoshizawa, A. 1984 Statistical analysis of the deviation of the Reynolds stress from its eddy-viscosity representation. Phys. Fluids 27, 1377.Google Scholar
Yoshizawa, A., Liou, W. W., Yokoi, N. & Shih, T. H. 1997 Modeling of compressible effects on the Reynolds stress using a Markovianized two-scale method. Phys. Fluids 9, 3024–3036.Google Scholar