Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2025-01-06T00:39:23.660Z Has data issue: false hasContentIssue false
  • English
  • Français

Mathematical modelling of a viscida network

Published online by Cambridge University Press:  07 June 2019

C. Mavroyiakoumou ,
I. M. Griffiths Open the ORCID record for I. M. Griffiths [Opens in a new window]  and
P. D. Howell
C. Mavroyiakoumou
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA
I. M. Griffiths*
Affiliation:
Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
P. D. Howell
Affiliation:
Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
*
†Email address for correspondence: ian.griffiths@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a general model to describe a network of interconnected thin viscous sheets, or viscidas, which evolve under the action of surface tension. A junction between two viscidas is analysed by considering a single viscida containing a smoothed corner, where the centreline angle changes rapidly, and then considering the limit as the smoothing tends to zero. The analysis is generalized to derive a simple model for the behaviour at a junction between an arbitrary number of viscidas, which is then coupled to the governing equation for each viscida. We thus obtain a general theory, consisting of 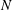$N$ partial differential equations and 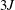$3J$ algebraic conservation laws, for a system of 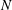$N$ viscidas connected at 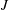$J$ junctions. This approach provides a framework to understand the fabrication of microstructured optical fibres containing closely spaced holes separated by interconnected thin viscous struts. We show sample solutions for simple networks with 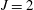$J=2$ and 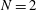$N=2$ or 3. We also demonstrate that there is no uniquely defined junction model to describe interconnections between viscidas of different thicknesses.

JFM classification

Interfacial Flows (free surface): Capillary flows Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 147 - 176
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birks, T. A., Knight, J. C. & Russell, P. S. J. 1997 Endlessly single-mode photonic crystal fiber. Opt. Lett. 22 (13), 961–963.Google Scholar
Buchak, P. & Crowdy, D. G. 2016 Surface-tension-driven Stokes flow: a numerical method based on conformal geometry. J. Comput. Phys. 317, 347–361.Google Scholar
Buchak, P., Crowdy, D. G., Stokes, Y. M. & Ebendorff-Heidepriem, H. 2015 Elliptical pore regularisation of the inverse problem for microstructured optical fibre fabrication. J. Fluid Mech. 778, 5–38.Google Scholar
Buckmaster, J. D. & Nachman, A. 1978 The buckling and stretching of a viscida II. Effects of surface tension. Q. J. Mech. Appl. Maths 31 (2), 157–168.Google Scholar
Buckmaster, J. D., Nachman, A. & Ting, L. 1975 The buckling and stretching of a viscida. J. Fluid Mech. 69 (01), 1–20.Google Scholar
Chen, M. J., Stokes, Y. M., Buchak, P., Crowdy, D. G. & Ebendorff-Heidepriem, H. 2015 Microstructured optical fibre drawing with active channel pressurisation. J. Fluid Mech. 783, 137–165.Google Scholar
Cummings, L. J. & Howell, P. D. 1999 On the evolution of non-axisymmetric viscous fibres with surface tension, inertia and gravity. J. Fluid Mech. 389, 361–389.Google Scholar
Dewynne, J. N., Howell, P. D. & Wilmott, P. 1994 Slender viscous fibres with inertia and gravity. Q. J. Mech. Appl. Maths 47 (4), 541–555.Google Scholar
Dewynne, J. N., Ockendon, J. R. & Wilmott, P. 1989 On a mathematical model for fiber tapering. SIAM J. Appl. Maths 49 (4), 983–990.Google Scholar
Ebendorff-Heidepriem, H. & Monro, T. M. 2007 Extrusion of complex preforms for microstructured optical fibers. Opt. Express 15 (23), 15086–15092.Google Scholar
Ebendorff-Heidepriem, H., Moore, R. C. & Monro, T. M. 2008 Progress in the fabrication of the next-generation soft glass microstructured optical fibers. AIP Conf. Proc. 1055 (1), 95–98.Google Scholar
Fitt, A. D., Furusawa, K., Monro, T. M., Please, C. P. & Richardson, D. J. 2002 The mathematical modelling of capillary drawing for holey fibre manufacture. J. Engng Maths 43 (2), 201–227.Google Scholar
Griffiths, I. M.2007 Mathematical modelling of non-axisymmetric glass tube manufacture. PhD thesis, University of Oxford.Google Scholar
Griffiths, I. M. & Howell, P. D. 2007 The surface-tension-driven evolution of a two-dimensional annular viscous tube. J. Fluid Mech. 593, 181–208.Google Scholar
Griffiths, I. M. & Howell, P. D. 2008 Mathematical modelling of non-axisymmetric capillary tube drawing. J. Fluid Mech. 605, 181–206.Google Scholar
Hansen, K. P., Broeng, J., Skovgaard, P. M., Folkenberg, J. R., Nielsen, M. D., Petersson, A., Hansen, T. P., Jakobsen, C., Simonsen, H. R., Limpert, J. et al. 2005 High-power photonic crystal fiber lasers: design, handling and subassemblies. Proc. SPIE 5709, 273–283.Google Scholar
Monro, T. M., Richardson, D. J., Broderick, N. G. R. & Bennett, P. J. 1999 Holey optical fibers: an efficient modal model. J. Lightwave Technol. 17 (6), 1093–1102.Google Scholar
Ranka, J. K., Windeler, R. S. & Stentz, A. J. 2000 Optical properties of high-delta air–silica microstructure optical fibers. Opt. Lett. 25 (11), 796–798.Google Scholar
Russell, P.2019 TDSU 3: Glass Studio. https://www.mpl.mpg.de/divisions/russell-division/research/tdsu-3-glass-studio/, accessed online 19 February 2019.Google Scholar
Senior, J. M. & Jamro, M. Y. 2009 Optical Fiber Communications: Principles and Practice. Pearson Education.Google Scholar
Stewart, P. S., Davis, S. H. & Hilgenfeldt, S. 2015 Microstructural effects in aqueous foam fracture. J. Fluid Mech. 785, 425–461.Google Scholar
Stokes, Y. M., Buchak, P., Crowdy, D. G. & Ebendorff-Heidepriem, H. 2014 Drawing of micro-structured fibres: circular and non-circular tubes. J. Fluid Mech. 755, 176–203.Google Scholar
Tronnolone, H.2016 Extensional and surface-tension-driven fluid flows in microstructured optical fibre fabrication. PhD thesis, University of Adelaide.Google Scholar
Wynne, R. M. 2006 A fabrication process for microstructured optical fibers. J. Lightwave Technol. 24 (11), 4304–4313.Google Scholar