Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-14T17:41:41.271Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximum drag enhancement asymptote in spanwise-rotating viscoelastic plane Couette flow of dilute polymeric solutions

Published online by Cambridge University Press:  01 March 2023

Yabiao Zhu Open the ORCID record for Yabiao Zhu [Opens in a new window] ,
Zhenhua Wan Open the ORCID record for Zhenhua Wan [Opens in a new window] ,
Fenghui Lin Open the ORCID record for Fenghui Lin [Opens in a new window] ,
Nansheng Liu Open the ORCID record for Nansheng Liu [Opens in a new window] ,
Xiyun Lu Open the ORCID record for Xiyun Lu [Opens in a new window]  and
Bamin Khomami Open the ORCID record for Bamin Khomami [Opens in a new window]
Yabiao Zhu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China Yangzhou Collaborative Innovation Research Institute, Shenyang ADRI, Yangzhou, Jiangsu 225000, PR China
Zhenhua Wan
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Fenghui Lin
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Nansheng Liu*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Xiyun Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Bamin Khomami*
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Tennessee, Knoxville, TN 37996, USA
*
†Email addresses for correspondence: lns@ustc.edu.cn, bkhomami@utk.edu
†Email addresses for correspondence: lns@ustc.edu.cn, bkhomami@utk.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

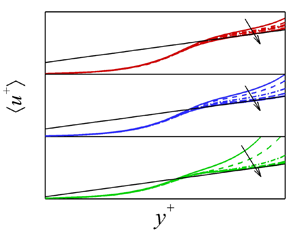
The existence of a maximum drag enhancement (MDE) asymptote at high rotation ($Ro$) and Weissenberg ($Wi$) numbers in turbulent viscoelastic spanwise-rotating plane Couette flow has been demonstrated. Specifically, it is shown that above a critical $Wi$, drag enhancement plateaus and the MDE asymptote is realized in a broad range of $Ro$. The mean velocity profiles at MDE appear to closely follow a log-law profile that has a nearly identical slope but different intercepts as a function of $Ro$. Much like the maximum drag reduction (MDR) asymptote, the logarithmic function in MDE is closely followed if the mean velocity is plotted using the traditional inner variable scaling; however, the logarithmic function is not well defined when examined by the indicator function. Hence, in this study, we have used the logarithmic fit as a visual guide for the mean velocity profile. Last and perhaps the most intriguing finding of this study is that MDE occurs in the elasto-inertial turbulence (EIT) flow state; hence, it is mainly sustained by elastic forces much like the MDR flow state. To that end, a universal picture of elastically induced drag modification asymptotes is emerging, namely these asymptotic states are an inherent property of the elastically sustained EIT flow state.

JFM classification

Non-Newtonian Flows: Viscoelasticity Turbulent Flows: Rotating turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 958 , 10 March 2023 , A15
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bech, K.H. & Andersson, H.I. 1996 Secondary flow in weakly rotating turbulent plane Couette flow. J. Fluid Mech. 317, 195–214.CrossRefGoogle Scholar
Brauckmann, H.J., Salewski, M. & Eckhardt, B. 2016 Momentum transport in Taylor–Couette flow with vanishing curvature. J. Fluid Mech. 790, 419–452.CrossRefGoogle Scholar
Choueiri, G.H., Lopez, J.M. & Hof, B. 2018 Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120 (12), 124501.CrossRefGoogle ScholarPubMed
De Angelis, E., Casciola, C.M. & Piva, R. 2002 DNS of wall turbulence: dilute polymers and self-sustaining mechanisms. Comput. Fluids 31, 495–507.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V.E., White, C.M., Shaqfeh, E.S., Moin, P. & Lele, S.K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74, 311–329.CrossRefGoogle Scholar
Elbing, B.R., Perlin, M.R., Dowling, D. & Ceccio, S.L. 2013 Modification of the mean near-wall velocity profile of a high-Reynolds number turbulent boundary layer with the injection of dragreducing polymer solutions. Phys. Fluids 25, 085103.CrossRefGoogle Scholar
Gai, J., Xia, Z., Cai, Q. & Chen, S. 2016 Turbulent statistics and flow structures in spanwise-rotating turbulent plane Couette flows. Phys. Rev. Fluids 1 (5), 054401.CrossRefGoogle Scholar
Kim, K., Li, C.-F., Sureshkumar, R., Balachandar, S. & Adrian, R.J. 2007 Effects of polymer stresses on eddy structures in drag-reduced turbulent channel flow. J. Fluid Mech. 584, 281–299.CrossRefGoogle Scholar
Li, C.-F., Sureshkumar, R. & Khomami, B. 2006 Influence of rheological parameters on polymer induced turbulent drag reduction. J. Non-Newtonian Fluid Mech. 140 (1–3), 23–40.CrossRefGoogle Scholar
Li, C.-F., Sureshkumar, R. & Khomami, B. 2015 Simple framework for understanding the universality of the maximum drag reduction asymptote in turbulent flow of polymer solutions. Phys. Rev. E 92, 043014.CrossRefGoogle ScholarPubMed
Liu, N. & Khomami, B. 2013 Polymer-induced drag enhancement in turbulent Taylor–Couette flows: direct numerical simulations and mechanistic insight. Phys. Rev. Lett. 111, 114501.CrossRefGoogle ScholarPubMed
Lopez, J.M., Choueiri, G.H. & Hof, B. 2019 Dynamics of viscoelastic pipe flow at low Reynolds numbers in the maximum drag reduction limit. J. Fluid Mech. 874, 699–719.CrossRefGoogle Scholar
Lumley, J.L. 1969 Drag reduction by additives. Annu. Rev. Fluid Mech. 1, 367–384.CrossRefGoogle Scholar
Ostilla, R., Verzicco, R. & Lohse, D. 2015 Effects of the computational domain size on direct numerical simulations of Taylor–Couette turbulence with stationary outer cylinder. Phys. Fluids 27, 025110.CrossRefGoogle Scholar
Ostilla, R., Verzicco, R. & Lohse, D. 2016 Turbulent Taylor–Couette flow with stationary inner cylinder. J. Fluid Mech. 766, R1.CrossRefGoogle Scholar
Procaccia, I., L'vov, V.S. & Benzi, R. 2008 Colloquium: theory of drag reduction by polymers in wall-bounded turbulence. Rev. Mod. Phys. 80, 225–247.CrossRefGoogle Scholar
Salewski, M. & Eckhardt, B. 2015 Turbulent states in plane Couette flow with rotation. Phys. Fluids 27 (4), 045109.CrossRefGoogle Scholar
Samanta, D., Dubief, Y., Holzner, M., Schäfer, C., Morozov, A.N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110 (26), 10557–10562.CrossRefGoogle ScholarPubMed
Serafini, F., Battista, F., Gualtieri, P. & Casciola, C.M. 2022 Drag reduction in turbulent wall-bounded flows of realistic polymer solutions. Phys. Rev. Lett. 129, 104502.CrossRefGoogle ScholarPubMed
Seyer, F.A. & Metzner, A.B. 1969 Turbulence phenomena in drag-reducing systems. AIChE J. 15, 426.CrossRefGoogle Scholar
Shaqfeh, E.S.G. & Khomami, B. 2021 The Oldroyd-B fluid in elastic instabilities, turbulence and particle suspensions. J. Non-Newtonian Fluid Mech. 298, 104672.CrossRefGoogle Scholar
Shekar, A., McMullen, R.M., Wang, S.-N., McKeon, B.J. & Graham, M.D. 2019 Critical-layer structures and mechanisms in elastoinertial turbulence. Phys. Rev. Lett. 122 (12), 124503.CrossRefGoogle ScholarPubMed
Sid, S., Terrapon, V.E. & Dubief, Y. 2018 Two-dimensional dynamics of elasto-inertial turbulence and its role in polymer drag reduction. Phys. Rev. Fluids 3 (1), 011301.CrossRefGoogle Scholar
Song, J., Lin, F., Liu, N., Lu, X. & Khomami, B. 2021 a Direct numerical simulation of inertio-elastic turbulent Taylor–Couette flow. J. Fluid Mech. 926, A37.CrossRefGoogle Scholar
Song, J., Teng, H., Liu, N., Ding, H., Lu, X. & Khomami, B. 2019 The correspondence between drag enhancement and vortical structures in turbulent Taylor–Couette flows with polymer additives: a study of curvature dependence. J. Fluid Mech. 881, 602–616.CrossRefGoogle Scholar
Song, J., Wan, Z., Liu, N., Lu, X. & Khomami, B. 2021 b A reverse transition route from inertial to elasticity-dominated turbulence in viscoelastic Taylor–Couette flow. J. Fluid Mech. 927, A10.CrossRefGoogle Scholar
Sureshkumar, R. & Beris, A.N. 1995 Effect of artificial stress diffusivity on the stability of numerical calculations and the flow dynamics of time-dependent viscoelastic flows. J. Non-Newtonian Fluid Mech. 60 (1), 53–80.CrossRefGoogle Scholar
Sureshkumar, R., Beris, A.N. & Handler, R.A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9 (3), 743–755.CrossRefGoogle Scholar
Teng, H., Liu, N., Lu, X. & Khomami, B. 2018 Turbulent drag reduction in plane Couette flow with polymer additives: a direct numerical simulation study. J. Fluid Mech. 846, 482–507.CrossRefGoogle Scholar
Toms, B.A. 1949 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the International Congress on Rheology, pp. 135–141. North Holland.Google Scholar
Virk, P.S. 1975 Drag reduction fundamentals. AIChE J. 21 (4), 625–656.CrossRefGoogle Scholar
White, C.M., Dubief, Y. & Klewicki, J. 2012 Re-examining the logarithmic dependence of the mean velocity distribution in polymer drag reduced wall-bounded flow. Phys. Fluids 24, 021701.CrossRefGoogle Scholar
White, C.M. & Mungal, M.G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.CrossRefGoogle Scholar
Zhu, Y., Song, J., Lin, F., Liu, N., Lu, X. & Khomami, B. 2022 Relaminarization of spanwise-rotating viscoelastic plane Couette flow via a transition sequence from a drag-reduced inertial to a drag-enhanced elasto-inertial turbulent flow. J. Fluid Mech. 931, R7.CrossRefGoogle Scholar
Zhu, Y., Song, J., Liu, N., Lu, X. & Khomami, B. 2020 Polymer-induced flow relaminarization and drag enhancement in spanwise-rotating plane Couette flow. J. Fluid Mech. 905, A19.CrossRefGoogle Scholar