Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T05:10:28.555Z Has data issue: false hasContentIssue false
  • English
  • Français

The mean electromotive force generated by elliptic instability

Published online by Cambridge University Press:  12 July 2012

K. A. Mizerski ,
K. Bajer  and
H. K. Moffatt
K. A. Mizerski*
Affiliation:
Department of Mechanics and Physics of Fluids, Institute of Fundamental Technological Research, Polish Academy of Sciences, ul. Pawińskiego 5B, 02-106, Warsaw, Poland
K. Bajer
Affiliation:
Faculty of Physics, University of Warsaw, ul. Pasteura 7, 02-093 Warsaw, Poland Interdisciplinary Centre for Mathematical and Computer Modelling, University of Warsaw, ul. Pawinskiego 5a, 02-106 Warsaw, Poland
H. K. Moffatt
Affiliation:
DAMTP, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: krzysztof.mizerski@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The mean electromotive force (EMF) associated with exponentially growing perturbations of an Euler flow with elliptic streamlines in a rotating frame of reference is studied. We are motivated by the possibility of dynamo action triggered by tidal deformation of astrophysical objects such as accretion discs, stars or planets. Ellipticity of the flow models such tidal deformations in the simplest way. Using analytical techniques developed by Lebovitz & Zweibel (Astrophys. J., vol. 609, 2004, pp. 301–312) in the limit of small elliptic (tidal) deformations, we find the EMF associated with each resonant instability described by Mizerski & Bajer (J. Fluid Mech., vol. 632, 2009, pp. 401–430), and for arbitrary ellipticity the EMF associated with unstable horizontal modes. Mixed resonance between unstable hydrodynamic and magnetic modes and resonance between unstable and oscillatory horizontal modes both lead to a non-vanishing mean EMF which grows exponentially in time. The essential conclusion is that interactions between unstable eigenmodes with the same wave-vector 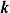can lead to a non-vanishing mean EMF, without any need for viscous or magnetic dissipation. This applies generally (and not only to the elliptic instabilities considered here).

JFM classification

MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD turbulence Instability: Parametric instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 111 - 128
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aldridge, K. D., Lumb, L. I. & Henderson, G. A. 1989 A Poincaré model for the earth’s fluid core. Geophys. Astrophys. Fluid Dyn. 48, 5–23.CrossRefGoogle Scholar
2. Bajer, K. & Mizerski, K. A. 2012 Elliptical flow instability triggered by a magnetic field. Phys. Rev. Lett. (submitted).Google Scholar
3. Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
4. Braginsky, S. I. 1964a Self excitation of a magnetic field during the motion of a highly conducting fluid. Sov. Phys. JETP 20, 726–735.Google Scholar
5. Braginsky, S. I. 1964b Theory of the hydromagnetic dynamo. Sov. Phys. JETP 20, 1462–1471.Google Scholar
6. Braginsky, S. I. 1975 An almost axially symmetric model of the hydromagnetic dynamo of the earth. Part I. Geomagn. Aeron. 15, 149–156.Google Scholar
7. Braginsky, S. I. 1976 On the nearly axially-symmetrical model of the hydromagnetic dynamo of the earth. Phys. Earth Planet. Inter. 11, 191–199.CrossRefGoogle Scholar
8. Braginsky, S. I. 1978 An almost axially symmetric model of the hydromagnetic dynamo of the earth. Part II. Geomagn. Aeron. 18, 240–351.Google Scholar
9. Bushby, P. J. & Proctor, M. R. E. 2010 The influence of -effect fluctuations and the shear-current effect upon the behaviour of solar mean-field dynamo models. Mon. Not. R. Astron. Soc. 409 (4), 1611–1618.CrossRefGoogle Scholar
10. Cambon, C., Benoit, J. P., Shao, L. & Jacquin, L. 1994 Stability analysis and large eddy simulation of rotating turbulence with organized eddies. J. Fluid Mech. 278, 175–200.CrossRefGoogle Scholar
11. Chandrasekhar, S. 1969 Ellipsoidal Figures of Equilibrium. Yale University Press.Google Scholar
12. Courvoisier, A., Hughes, D. W. & Tobias, S. M. 2006 -effect in a family of chaotic flows. Phys. Rev. Lett. 96, 034503.CrossRefGoogle Scholar
13. Craik, A. D. D. & Criminale, W. O. 1986 Evolution of wavelike disturbances in shear flows: a class of exact solutions of the Navier–Stokes equations. Proc. R. Soc. A 406 (1830), 13–26.Google Scholar
14. Gilbert, A. 2003 Dynamo theory. In Handbook of Mathematical Fluid Dynamics (ed. Friedlander, S. & Serre, D. ), vol. 2, pp. 355–441. Elsevier.CrossRefGoogle Scholar
15. Hawley, J. F., Gammie, C. F. & Balbus, S. A. 1995 Local three-dimensional magnetohydrodynamic simulations of accretion disks. Astrophys. J. 440, 742–763.CrossRefGoogle Scholar
16. Kerswell, R. R. 1993 The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 72 (1), 107–144.CrossRefGoogle Scholar
17. Kerswell, R. R. 1994 Tidal excitation of hydromagnetic waves and their damping in the earth. J. Fluid Mech. 274, 219–241.CrossRefGoogle Scholar
18. Kerswell, R. R. & Malkus, W. V. R. 1998 Tidal instability as the source for Io’s magnetic signature. Geophys. Res. Lett. 25 (5), 603–606.CrossRefGoogle Scholar
19. Lacaze, L., Le Gal, P. & Le Dizès, S. 2004 Elliptical instability in a rotating spheroid. J. Fluid Mech. 505, 1–22.CrossRefGoogle Scholar
20. Lacaze, L., Le Gal, P. & Le Dizès, S. 2005 Elliptical instability of the flow in a rotating shell. Phys. Earth Planet. Inter. 151 (3/4), 194–205.CrossRefGoogle Scholar
21. Lacaze, L., Herreman, W., Le Bars, M., Le Dizès, S. & Le Gal, P. 2006 Magnetic field induced by elliptical instability in a rotating spheroid. Geophys. Astrophys. Fluid Dyn. 100 (4/5), 299–317.CrossRefGoogle Scholar
22. Landman, M. J. & Saffman, P. G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30 (8), 2339–2342.CrossRefGoogle Scholar
23. Leblanc, S. & Cambon, C. 1997 On the three-dimensional instabilities of plane flows subjected to Coriolis force. Phys. Fluids 9 (5), 1307–1316.CrossRefGoogle Scholar
24. Leblanc, S. 1997 Stability of stagnation points in rotating flows. Phys. Fluids 9 (11), 3566–3569.CrossRefGoogle Scholar
25. Lebovitz, N. R. & Lifschitz, A. 1996 Short wavelength instabilities of Riemann ellipsoids. Phil. Trans. R. Soc. Lond. A 354, 927–950.Google Scholar
26. Lebovitz, N. R. & Zweibel, E. 2004 Magnetoelliptic instabilities. Astrophys. J. 609, 301–312.CrossRefGoogle Scholar
27. Le Gal, P., Lacaze, L. & Le Dizès, S. 2005 Magnetic field induced by elliptical instability in a rotating tidally-distorted sphere. J. Phys. Conf. Ser. 14, 30–34.CrossRefGoogle Scholar
28. Lesur, G. & Papaloizou, J. C. B. 2009 On the stability of elliptical vortices in accretion discs. Astron. Astrophys. 498, 1–12.CrossRefGoogle Scholar
29. Malkus, W. V. R. 1968 Precession of the earth as the cause of geomagnetism: experiments lend support to the proposal that precessional torques drive the earth’s dynamo. Science 160 (3825), 259–264.CrossRefGoogle Scholar
30. Malkus, W. V. R. 1989 An experimental study of global instabilities due to the tidal (elliptical) distortion of a rotating elastic cylinder. Geophys. Astrophys. Fluid Dyn. 48 (1), 123–134.CrossRefGoogle Scholar
31. Mizerski, K. A. & Bajer, K. 2009 The magnetoelliptic instability of rotating systems. J. Fluid Mech. 632 (1), 401–430.CrossRefGoogle Scholar
32. Mizerski, K. A. & Bajer, K. 2011 The influence of magnetic field on short-wavelength instability of Riemann ellipsoids. Physica D 240, 1629–1635.CrossRefGoogle Scholar
33. Moffatt, H. K. 1970 Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44, 705–719, available at http://moffatt.tc.CrossRefGoogle Scholar
34. Moffatt, H. K. 1974 The mean electromotive force generated by turbulence in the limit of perfect conductivity. J. Fluid Mech. 65, 1–10, available at http://moffatt.tc.CrossRefGoogle Scholar
35. Moffatt, H. K. 1976 Generation of magnetic fields by fluid motion. Adv. Appl. Mech. 16, 119–181, available at http://moffatt.tc.CrossRefGoogle Scholar
36. Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press, available at http://moffatt.tc.Google Scholar
37. Moffatt, H. K. 1983 Induction in turbulent conductors. In Stellar and Planetary Magnetism (ed. Soward, A. M. ). pp. 3–16. Gordon and Breach, available at http://moffatt.tc.Google Scholar
38. Noir, J., Brito, D., Aldridge, K. & Cardin, P. 2001 Experimental evidence of inertial waves in a precessing spheroidal cavity. Geophys. Res. Lett. 28 (19), 3785–3788.CrossRefGoogle Scholar
39. Proctor, M. R. E. 2007 Effects of fluctuation on alpha–omega dynamo models. Mon. Not. R. Astron. Soc. 382 (1), L39–L42.CrossRefGoogle Scholar
40. Rädler, K. H. & Brandenburg, A. 2009 Mean-field effects in the Galloway–Proctor flow. Mon. Not. R. Astron. Soc. 393 (1), 113–125.CrossRefGoogle Scholar
41. Richardson, K. J. & Proctor, M. R. E. 2010 Effects of -effect fluctuations on simple nonlinear dynamo models. Geophys. Astrophys. Fluid Dyn. 104 (5), 601–618.CrossRefGoogle Scholar
42. Roberts, G. O. 1972 Dynamo action of fluid motions with two-dimensional periodicity. Phil. Trans. R. Soc. A 271 (1216), 411–454.Google Scholar
43. Rüdiger, G. O. & Hollerbach, R. 2004 The Magnetic Universe: Geophysical and Astrophysical Dynamo Theory. Wiley.CrossRefGoogle Scholar
44. Seehafer, N. 1995 The turbulent electromotive force in the high-conductivity limit. Astron. Astrophys. 301, 290–292.Google Scholar
45. Soward, A. M. 1972 A kinematic theory of large magnetic Reynolds number dynamos. Phil. Trans. R. Soc. A 272 (1227), 431–462.Google Scholar
46. Suess, S. T. 1970 Some effects of gravitational tides on a model earth’s core. J. Geophys. Res. 75, 6650–6661.CrossRefGoogle Scholar
47. Tilgner, A. 2005 Precession driven dynamos. Phys. Fluids 17, 034104.CrossRefGoogle Scholar
48. Vanyo, J., Wilde, P., Cardin, P. & Olson, P. 1995 Experiments on precessing flows in the Earth’s liquid core. Geophys. J. Intl 121 (1), 136–142.CrossRefGoogle Scholar
49. Wienbruch, U. & Spohn, T. 1995 A self sustained magnetic field on Io?. Planet. Space Sci. 43 (9), 1045–1057.CrossRefGoogle Scholar