Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T06:53:52.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean flow generation by an intermittently unstable boundary layer over a sloping wall

Published online by Cambridge University Press:  22 August 2018

Abouzar Ghasemi Open the ORCID record for Abouzar Ghasemi [Opens in a new window] ,
Marten Klein ,
Andreas Will  and
Uwe Harlander
Abouzar Ghasemi*
Affiliation:
Department for Atmospheric and Environmental Sciences, Goethe University of Frankfurt am Main, Frankfurt/Main, Germany
Marten Klein
Affiliation:
Department of Numerical Fluid and Gas Dynamics, Brandenburg University of Technology (BTU) Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
Andreas Will
Affiliation:
Department of Environmental Meteorology, Brandenburg University of Technology (BTU) Cottbus-Senftenberg, Burger Chaussee 2, D-03044 Cottbus, Germany
Uwe Harlander
Affiliation:
Department of Aerodynamics and Fluid Mechanics, Brandenburg University of Technology (BTU) Cottbus-Senftenberg, Siemens-Halske-Ring 14, D-03046 Cottbus, Germany
*
†Email address for correspondence: ghasemi@iau.uni-frankfurt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of the flow in various rotating annular confinements have been conducted to investigate the effects of wall inclination on secondary fluid motions due to an unstable boundary layer. The inner wall resembles a truncated cone (frustum) whose apex half-angle is varied from 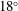$18^{\circ }$ to 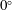$0^{\circ }$ (straight cylinder). The large inner radius 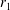$r_{1}$, the mean rotation rate 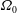$\unicode[STIX]{x1D6FA}_{0}$ and the kinematic viscosity $\unicode[STIX]{x1D708}$ were kept constant resulting in the constant Ekman number 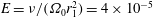$E=\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FA}_{0}r_{1}^{2})=4\times 10^{-5}$. Flows were excited by time-harmonic modulation of the inner wall’s rotation rate (so-called longitudinal libration) by prescribing the amplitude 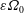$\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FA}_{0}$ and the forcing frequency 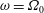$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FA}_{0}$. By steepening the inner wall and hence reducing the effect of the local Coriolis force in the boundary layer three different flow regimes can be realized: a rotation-dominated, a libration-dominated and an intermediate regime. In the present study we focus on the libration-dominated regime. For small libration amplitudes (here 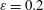$\unicode[STIX]{x1D700}=0.2$), a laminar Ekman–Stokes boundary layer (ESBL) is realized at the librating wall. With the aid of laminar boundary layer theory and DNS we show that the ESBL exhibits an oscillatory mass flux along the librating wall (Ekman property) and an oscillatory azimuthal velocity, which resembles a radially damped wave (Stokes property). For large libration amplitudes (here $\unicode[STIX]{x1D700}=0.8$), the DNS results exhibit an intermittently unstable ESBL, which turns centrifugally unstable during the prograde (faster) part of a libration period. This instability is due to the Stokes property and gives rise to Görtler vortices, which are found to be tilted with respect to the azimuth when the librating wall is at a finite angle relative to the axis of rotation. We show that this tilt is related to the Ekman property of the ESBL. This suggests that linear and nonlinear dynamics are equally important for this intermittent instability. Our DNS results indicate further that the Görtler vortices propagate into the fluid bulk where they generate an azimuthal mean flow. This mean flow is notably different from the mean flow driven in the case of the stable ESBL. A diagnostic analysis of the Reynolds-averaged Navier–Stokes (RANS) equations in the unstable flow regime hints at a competition between the radial and axial turbulent transport terms which act as generating and destructing agents for the azimuthal mean flow, respectively. We show that the balance of both terms depends on the wall inclination, that is, on the wall-tangential component of the Coriolis force.

JFM classification

Instability: Instability Turbulent Flows: Intermittency Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 111 - 149
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldridge, K. D.1967 An experimental study of axisymmetric inertial oscillations of a rotating sphere. PhD thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts.Google Scholar
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., McKenney, A. & Sorensen, D. 1999 LAPACK Users’ Guide, 3rd edn. Society for Industrial and Applied Mathematics.Google Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108, 124501.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bilson, M. & Bremhorst, K. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 579, 227–270.Google Scholar
Borcia, I. D., Ghasemi, V. A. & Harlander, U. 2014 Inertial wave mode excitation in a rotating annulus with partially librating boundaries. Fluid Dyn. Res. 46, 041423.Google Scholar
Borcia, I. D. & Harlander, U. 2012 Inertial waves in a rotating annulus with inclined inner cylinder: comparing the spectrum of wave attractor frequency bands and the eigenspectrum in the limit of zero inclination. Theor. Comput. Fluid Dyn. 27, 397–413.Google Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.Google Scholar
Busse, F. H. 2011 Zonal flow induced by longitudinal librations of a rotating cylindrical cavity. Physica D Nonlinear Phenomena 240 (2), 208–211.Google Scholar
Busse, F. H., Dormy, E., Simitev, R. & Soward, A. M. 2007 Mathematical Aspects of Natural Dynamos. Grenoble Sciences and CRC Press.Google Scholar
Busse, F. H. & Or, A. C. 1986 Subharmonic and asymmetric convection rolls. Z. Angew. Math. Phys. J. Appl. Math. Phys. 37, 608–623.Google Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22 (8), 086602.Google Scholar
Chemin, J.-Y., Desjardins, B., Gallagher, I. & Grenier, E. 2006 Mathematical Geophysics. Clarendon Press.Google Scholar
Choi, H., Moin, P. & Kim, J.1992 Turbulent drag reduction: studies of feedback control and flow over riblets. Tech. Rep. TF-55. Department of Mechanical Engineering, Stanford University, Stanford, CA.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulations of turbulent-flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Comstock, R. L. & Bills, B. G. 2003 A solar system survey of forced librations in longitude. J. Geophys. Res. 108 (E9), 5100.Google Scholar
Czarny, O. & Lueptow, R. M. 2007 Time scales for transition in Taylor–Couette flow. Phys. Fluids 19, 054103.Google Scholar
Ekman, V. W. 1905 On the influence of Earth’s rotation on ocean currents. Arkiv för Matematik, Astronomi och Fysik 2, 1–52.Google Scholar
Ghasemi, A.2017 Mean flow generation mechanisms in a rotating annular container with librating walls. PhD thesis, Fakultät für Umwelt und Naturwissenschaften, Brandenburgische Technische Universität Cottbus-Senftenberg, Cottbus, Germany, published by Cuvillier Verlag Göttingen, Germany.Google Scholar
Ghasemi, A., Klein, M., Harlander, U., Kurgansky, M. V., Schaller, E. & Will, A. 2016 Mean flow generation by Görtler vortices in a rotating annulus with librating side-walls. Phys. Fluids 28 (5), 056603.Google Scholar
Greenspan, H. P. 1969 The Theory of Rotating Fluids. Cambridge University Press; reprint with corrections.Google Scholar
Hazewinkel, J., Maas, L. R. M. & Dalziel, S. B. 2008 Observations on the wavenumber spectrum and evolution of an internal wave attractor. J. Fluid Mech. 598, 373–382.Google Scholar
Henderson, G. A. & Aldridge, K. D. 1992 A finite-element method for inertial waves in a frustum. J. Fluid Mech. 234, 317–327.Google Scholar
Hoff, M., Harlander, U. & Triana, S. A. 2016 Study of turbulence and interacting inertial modes in a differentially rotating spherical shell experiment. Phys. Rev. Fluids 1, 043701.Google Scholar
Hollerbach, R. & Fournier, A. 2004 End-effects in rapidly rotating cylindrical Taylor–Couette flow. In MHD Couette Flows: Experiments and Models (ed. Bonanno, A., Rüdiger, G. & Rosner, R.), vol. 733, pp. 114–121. AIP Conference proceedings.Google Scholar
Jouve, L. & Ogilvie, G. I. 2014 Direct numerical simulations of an inertial wave attractor in linear and nonlinear regimes. J. Fluid Mech. 745, 223–250.Google Scholar
Kaltenbach, H.-J., Fatica, M., Mittal, R., Lund, T. S. & Moin, P. 1999 Study of flow in a planar asymmetric diffuser using large-eddy simulation. J. Fluid Mech. 390, 151–185.Google Scholar
Kerswell, R. R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59 (2), 308–323.Google Scholar
Klein, M.2016 Inertial wave attractors, resonances, and wave excitation by libration: direct numerical simulations and theory. PhD thesis, Fakultät für Umwelt und Naturwissenschaften, Brandenburgische Technische Universität Cottbus-Senftenberg, Cottbus, Germany, published online.Google Scholar
Klein, M., Seelig, T., Kurgansky, M. V., Ghasemi, A., Borcia, I. D., Will, A., Schaller, E., Egbers, C. & Harlander, U. 2014 Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder. J. Fluid Mech. 751, 255–297.Google Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45 (3), 035504.Google Scholar
Lopez, J. M. & Marques, F. 2011 Instabilities and inertial waves generated in a librating cylinder. J. Fluid Mech. 687, 171–193.Google Scholar
Lund, T. S. & Kaltenbach, H.-J.1995 Experiments with explicit filtering for LES using a finite-difference method. Annual Research Briefs 1995. Center for Turbulence Research, Stanford, CA.Google Scholar
Maas, L. R. M. 2001 Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 437, 13–28.Google Scholar
Maas, L. R. M. & Lam, F.-P. A. 1995 Geometric focusing of internal waves. J. Fluid Mech. 300, 1–41.Google Scholar
Morinishi, Y., Lund, T. S., Vasilyev, V. O. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143 (1), 90–124.Google Scholar
Noir, J., Calkins, M. A., Lasbleis, M., Cantwell, J. & Aurnou, J. M. 2010 Experimental study of libration-driven zonal flows in a straight cylinder. Phys. Earth Planet. Inter. 182, 98–106.Google Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173, 141–152.Google Scholar
Nordsiek, F., Huisman, S. G., van der Veen, R. C. A., Sun, C., Lohse, D. & Lathrop, D. A. 2015 Azimuthal velocity profiles in Rayleigh-stable Taylor–Couette flow and implied axial angular momentum transport. J. Fluid Mech. 774, 342–362.Google Scholar
Orlandi, P. 2000 Fluid Flow Phenomena: A Numerical Toolkit. Kluwer.Google Scholar
Orszag, S. A. 1971 On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28, 1074.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26, 015114.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Prandle, D. 1982 The vertical structure of tidal currents and other oscillatory flows. Cont. Shelf Res. 1 (2), 191–207.Google Scholar
Salon, S. & Armenio, V. 2011 A numerical investigation of the turbulent Stokes–Ekman bottom boundary layer. J. Fluid Mech. 684, 316–352.Google Scholar
Sauret, A., Cébron, D. & Le Bars, M. 2013 Sponateous generation of inertial waves from boundary turbulence in a librating sphere. J. Fluid Mech. 728 (R5), 1–11.Google Scholar
Sauret, A., Cébron, D., Le Bars, M. & Le Dizès, S. 2012 Fluid flows in a librating cylinder. Phys. Fluids 24, 026603.Google Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.Google Scholar
Swart, A., Manders, A., Harlander, U. & Maas, L. R. M. 2010 Experimental observation of strong mixing due to internal wave focusing over sloping terrain. Dyn. Atmos. Oceans 50, 16–34.Google Scholar
Thompson, J. E., Warsi, Z. U. A. & Mastin, C. W. 1985 Numerical Grid Generation: Foundations and Applications. North-Holland.Google Scholar
Thorade, H. 1928 Gezeitenuntersuchungen in der Deutschen Bucht der Nordsee. Deutsche Seewarte 46 (3), 1–85.Google Scholar
Wang, C.-Y. 1970 Cylindrical tank of fluid oscillating about a state of steady rotation. J. Fluid Mech. 41, 581–592.Google Scholar