Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T15:47:16.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean flow structure in horizontal convection

Published online by Cambridge University Press:  05 January 2017

Olga Shishkina Open the ORCID record for Olga Shishkina [Opens in a new window]
Olga Shishkina*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, D-37077 Göttingen, Germany
*
†Email address for correspondence: Olga.Shishkina@ds.mpg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

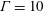We analyse the global flow structures in horizontal convection systems, where the heat supply and removal takes place through separated parts of a lower horizontal surface of a fluid layer. The results are based on direct numerical simulations for the length-to-height aspect ratio of the convection cell $\unicode[STIX]{x1D6E4}=10$, Rayleigh number 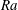$\mathit{Ra}$ from 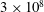$3\times 10^{8}$ to 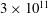$3\times 10^{11}$ and Prandtl number 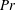$\mathit{Pr}$ from 0.05 to 50. The structure of the mean flows in horizontal convection is described in terms of time-averaged spatial distributions of the temperature, velocity, kinetic energy, thermal and kinetic dissipation rates. A possible scenario of transition to turbulent horizontal convection in the whole convection cell of a large aspect ratio is discussed.

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 525 - 540
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.Google Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google ScholarPubMed
Chiu-Webster, S., Hinch, E. J. & Liter, J. R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.CrossRefGoogle Scholar
Cushman-Roisin, B. & Beckers, J.-M. 2011 Introduction to Geophysical Fluid Dynamics. Physical and Numerical Aspects, 2nd edn. Academic.Google Scholar
Daya, Z. A. & Ecke, R. E. 2001 Does turbulent convection feel the shape of the container? Phys. Rev. Lett. 87, 184501.Google Scholar
Gayen, B., Griffiths, R. W. & Hughes, G. O. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 698–724.CrossRefGoogle Scholar
Gibert, M., Pabiou, H., Chillà, F. & Castaing, B. 2006 High-Rayleigh-number convection in a vertical channel. Phys. Rev. Lett. 96, 084501.Google Scholar
Gramberg, H. J. J., Howell, P. D. & Ockendon, J. R. 2007 Convection by a horizontal thermal gradient. J. Fluid Mech. 586, 41–57.Google Scholar
Griffiths, R. W., Hughes, G. O. & Gayen, B. 2013 Horizontal convection dynamics: insights from transient adjustment. J. Fluid Mech. 726, 559–595.Google Scholar
Griffiths, R. W., Maher, N. & Hughes, G. O. 2011 Horizontal convection under oscillatory buoyancy forcing. J. Mar. Res. 69, 523–543.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Hanasoge, S., Gizon, L. & Sreenivasan, K. R. 2016 Seismic sounding of convection in the sun. Annu. Rev. Fluid Mech. 48, 191–217.CrossRefGoogle Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Horn, S. & Shishkina, O. 2015 Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255.Google Scholar
Houghton, J. T. 1977 The Physics of Atmospheres. Cambridge University Press.Google Scholar
Huang, S.-D., Wang, F., Xi, H.-D. & Xia, K.-Q. 2015 Comparative experimental study of fixed temperature and fixed heat flux boundary conditions in turbulent thermal convection. Phys. Rev. Lett. 115, 154502.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Ng, C. S., Ooi, A., Lohse, D. & Chung, D. 2015 Vertical natural convection: application of the unifying theory of thermal convection. J. Fluid Mech. 764, 349–361.CrossRefGoogle Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep Sea Res. 12, 9–16.Google Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really ‘non-turbulent’? Geophys. Res. Lett. 38, L21609.CrossRefGoogle Scholar
Sheard, G. J. & King, M. P. 2011 Horizontal convection: effect of aspect ratio on Rayleigh number scaling and stability. Appl. Math. Model. 35, 1647.Google Scholar
Shishkina, O. 2007 The Neumann stability of high-order symmetric schemes for convection–diffusion problems. Sib. Math. J. 48, 1141–1146.Google Scholar
Shishkina, O. 2016 Momentum and heat transport scalings in laminar vertical convection. Phys. Rev. E 93, 051102 (R).Google Scholar
Shishkina, O., Grossmann, S. & Lohse, D. 2016 Heat and momentum transport scalings in horizontal convection. Geophys. Res. Lett. 43, 1219–1225.Google Scholar
Shishkina, O. & Horn, S. 2016 Thermal convection in inclined cylindrical containers. J. Fluid Mech. 790, R3.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Shishkina, O. & Wagner, S. 2016 Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett. 116, 024302.CrossRefGoogle ScholarPubMed
Siggers, J. H., Kerswell, R. R. & Balmforth, N. J. 2004 Bounds on horizontal convection. J. Fluid Mech. 517, 55–70.Google Scholar
Song, H. & Tong, P. 2010 Scaling laws in turbulent Rayleigh–Bénard convection under different geometry. Eur. Phys. Lett. 90, 44001.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Wang, W. & Huang, R. X. 2005 An experimental study on thermal circulation driven by horizontal differential heating. J. Fluid Mech. 540, 49–73.CrossRefGoogle Scholar
Yu, H., Li, N. & Ecke, R. E. 2007 Scaling in laminar natural convection in laterally heated cavities: is turbulence essential in the classical scaling of heat transfer? Phys. Rev. E 76, 026303.Google Scholar