Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-28T03:17:46.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Mechanism for frustum transition over blunt cones at hypersonic speeds

Published online by Cambridge University Press:  11 May 2020

Pedro Paredes Open the ORCID record for Pedro Paredes [Opens in a new window] ,
Meelan M. Choudhari Open the ORCID record for Meelan M. Choudhari [Opens in a new window]  and
Fei Li
Pedro Paredes*
Affiliation:
National Institute of Aerospace, Hampton, VA 23666, USA
Meelan M. Choudhari
Affiliation:
NASA Langley Research Center, Hampton, VA 23681, USA
Fei Li
Affiliation:
NASA Langley Research Center, Hampton, VA 23681, USA
*
†Email address for correspondence: pedro.paredes@nasa.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

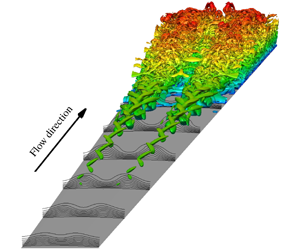
Numerical and experimental studies have demonstrated laminar–turbulent transition in hypersonic boundary layers over sharp cones via the modal growth of planar Mack-mode instabilities. However, due to the strong reduction in Mack-mode growth at higher nose bluntness values, the mechanisms underlying the observed onset of transition over the cone frustum are currently unknown. Linear non-modal growth analysis has shown that both planar and oblique travelling disturbances that peak within the entropy layer experience appreciable energy amplification for moderate to large nose bluntness. However, due to their weak signature within the boundary-layer region, the route to transition onset via non-modal growth of travelling disturbances remains unclear. Nonlinear parabolized stability equations (NPSE) and direct numerical simulations (DNS) are used to identify a potential mechanism for transition over a 7-degree blunt cone that was tested in the AFRL Mach-6 high-Reynolds-number facility. Specifically, computations are conducted to study the nonlinear development of a pair of oblique, unsteady non-modal disturbances in the regime of moderately blunt nose tips. Excellent agreement was demonstrated between the NPSE and DNS predictions. Results reveal that, even though the linear non-modal disturbances are primarily concentrated outside the boundary layer, their nonlinear interaction can generate stationary streaks that penetrate and amplify within the boundary layer, eventually inducing the onset of transition via the breakdown of these streaks. The results indicate that a pair of oblique, controlled non-modal disturbances can produce transition at the location measured in the experiment when their initial amplitude is chosen to be approximately 0.15 % of the free-stream velocity.

JFM classification

Aerodynamics: High-speed flow Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 894 , 10 July 2020 , A22
Creative Commons
Creative Common License - CCCreative Common License - BY
This is a work of the US Government and is not subject to copyright protection within the United States.
Copyright
© National Institute of Aerospace Associates and United States Government as Represented by the Administrator of the National Aeronautics and Space Administration, 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, N. A. & Kleiser, L. 1993 Numerical simulation of transition in a compressible flat plate boundary layer. In Transitional and Turbulent Compressible Flows (ed. Kral, L. D. & Zang, T. A.), pp. 101–110. ASME, No. 151 in FED.Google Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11, 134–150.CrossRefGoogle Scholar
Berlin, S., Lundbladh, A. & Henningson, D. S. 1994 Spatial simulations of oblique transition in a boundary layer. Phys. Fluids 6 (6), 1949–1951.CrossRefGoogle Scholar
Chang, C.-L. & Malik, M. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–360.CrossRefGoogle Scholar
Chu, B.-T. 1956 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mech. 1 (3), 215–234.CrossRefGoogle Scholar
Cook, D. A., Thome, J. S., Brock, J. M., Nichols, J. W. & Candler, G. V.2018 Understanding effects of nose-cone bluntness on hypersonic boundary layer transition using input-output analysis. AIAA Paper 2018-0378.CrossRefGoogle Scholar
Dietz, G. & Hein, S. 1999 Entropy-layer instabilities over a blunted flat plate in supersonic flow. Phys. Fluids 11 (1), 7–9.CrossRefGoogle Scholar
Fasel, H., Thumm, A. & Bestek, H. 1993 Direct numerical simulation of transition in supersonic boundary layer: oblique breakdown. In Transitional and Turbulent Compressible Flows (ed. Kral, L. D. & Zang, T. A.), pp. 77–92. ASME, No. 151 in FED.Google Scholar
Fedorov, A. & Tumin, A. 2004 Evolution of disturbances in entropy layer on blunted plate in supersonic flow. AIAA J. 42 (1), 89–94.CrossRefGoogle Scholar
Grossir, G., Pinna, F., Bonucci, G., Regert, T., Rambaut, P. & Chazot, O.2014 Hypersonic boundary layer transition on a 7 degree half-angle cone at Mach 10. AIAA Paper 2014-2774.CrossRefGoogle Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20, 487–526.CrossRefGoogle Scholar
Hermanns, M. & Hernández, J. A. 2008 Stable high-order finite-difference methods based on non-uniform grid point distributions. Intl J. Numer. Meth. Fluids 56, 233–255.CrossRefGoogle Scholar
Jewell, J. S., Kennedy, R. E., Laurence, S. J. & Kimmel, R. L.2018 Transition on a variable bluntness 7-degree cone at high Reynolds number. AIAA Paper 2018-1822.CrossRefGoogle Scholar
Jewell, J. S. & Kimmel, R. L. 2017 Boundary layer stability analysis for Stetson’s Mach 6 blunt cone experiments. J. Spacecr. Rockets 54 (1), 258–265.CrossRefGoogle Scholar
Jiang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Joslin, R. D., Streett, C. L. & Chang, C.-L. 1992 Oblique-wave breakdown in an incompressible boundary layer computed by spatial DNS and PSE theory. In Instability, Transition, and Turbulence (ed. Hussaini, M. Y., Kumar, A. & Streett, C. L.), pp. 304–310. Springer.CrossRefGoogle Scholar
Kara, K., Balakumar, P. & Kandil, O. A. 2011 Effects of nose bluntness on hypersonic boundary-layer receptvity and stability over cones. AIAA J. 49 (12), 2593–2606.CrossRefGoogle Scholar
Kennedy, R. E., Jagde, E. K., Laurence, S. J., Jewell, J. S. & Kimmel, R. L.2019 Visualizations of hypersonic boundary-layer transition on a variable bluntness cone. AIAA Paper 2019-3079.CrossRefGoogle Scholar
Kufner, E., Dallmann, U. & Stilla, J.1993 Instability of hypersonic flow past blunt cones – effects of mean flow variations. AIAA Paper 93-2983.CrossRefGoogle Scholar
Laible, A. C. & Fasel, H. F. 2016 Continuously forced transient growth in oblique breakdown for supersonic boundary layers. J. Fluid Mech. 804, 323–350.CrossRefGoogle Scholar
Laible, A. C., Mayer, C. S. J. & Fasel, H. F.2009 Numerical investigation of transition for a cone at Mach 3.5. AIAA Paper 2009-3557.CrossRefGoogle Scholar
Leib, S. J., Wundrow, D. W. & Goldstein, M. E. 1999 Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 380, 169–203.CrossRefGoogle Scholar
Mack, L. M.1969 Boundary layer stability theory. Tech. Rep. Jet Propulsion Laboratory Report 900-277. California Institute of Technology, Pasadena, CA.Google Scholar
Malik, M. R., Spall, R. E. & Chang, C.-L.1990 Effect of nose bluntness on boundary layer stability and transition. AIAA Paper 90-0112.CrossRefGoogle Scholar
Marineau, E. C., Moraru, C. G., Lewis, D. R., Norris, J. D., Lafferty, J. F., Wagnild, R. M. & Smith, J. S.2014 Mach 10 boundary-layer transition experiments on sharp and blunted cones. AIAA Paper 2014-3108.CrossRefGoogle Scholar
Martin, J. A. & Paredes, P. 2016 Three-dimensional instability analysis of boundary layers perturbed by streamwise vortices. Theor. Comput. Fluid Dyn. 31 (5–6), 505–517.CrossRefGoogle Scholar
Martin, M. P., Taylor, E. M., Wu, M. & Weirs, V. G. 2006 A bandwidth-optimized WENO scheme for the direct numerical simulation of compressible turbulence. J. Comput. Phys. 220 (1), 270–289.CrossRefGoogle Scholar
Mayer, C. S. J., Von Terzi, D. A. & Fasel, H. F. 2011 Direct numerical simulation of complete transition to turbulence via oblqiue breakdown at Mach 3. J. Fluid Mech. 674, 5–42.CrossRefGoogle Scholar
Ovchinnikov, V., Choudhari, M. M. & Piomelli, U. 2008 Numerical simulations of boundary-layer bypass transition due to high-amplitude free-stream turbulence. J. Fluid Mech. 613, 135–169.CrossRefGoogle Scholar
Panina, A. V., Kosinov, A. D., Semionov, N. V. & Yermolaev, Y. G. 2017 On the oblique breakdown mechanism in a supersonic boundary layer on a swept wing at Mach 2. AIP Conf. Proc. 1893 (1), 030080.CrossRefGoogle Scholar
Paredes, P., Choudhari, M. & Li, F. 2017 Instaiblity wave-streak interactions in a supersonic boundary layer. J. Fluid Mech. 831, 524–553.CrossRefGoogle Scholar
Paredes, P., Choudhari, M. & Li, F. 2019a Instaiblity wave-streak interactions in a high Mach number boundary layer at flight conditions. J. Fluid Mech. 858, 474–499.CrossRefGoogle Scholar
Paredes, P., Choudhari, M. & Li, F.2019b Laminar-turbulent transition upstream of the entropy-layer swallowing location in hypersonic boundary layers. AIAA Paper 2019-3215.CrossRefGoogle Scholar
Paredes, P., Choudhari, M., Li, F., Jewell, J. & Kimmel, R. 2019c Nonmodal growth of traveling waves on blunt cones at hypersonic speeds. AIAA J. 57 (11), 4738–4749.CrossRefGoogle Scholar
Paredes, P., Choudhari, M., Li, F., Jewell, J. S., Kimmel, R. L., Marineau, E. C. & Grossir, G.2018 Nosetip bluntness effects on transition at hypersonic speeds: experimental and numerical analysis under NATO STO AVT-240. AIAA Paper 2018-0057.CrossRefGoogle Scholar
Paredes, P., Choudhari, M., Li, F., Jewell, J., Kimmel, R., Marineau, E. & Grossir, G. 2019d Nosetip bluntness effects on transition at hypersonic speeds: experimental and numerical analysis. J. Spacecr. Rockets 56 (2), 369–387.CrossRefGoogle Scholar
Paredes, P., Hanifi, A., Theofilis, V. & Henningson, D. 2015 The nonlinear PSE-3D concept for transition prediction in flows with a single slowly-varying spatial direction. Procedia IUTAM 14C, 35–44.Google Scholar
Schmid, P. J. & Henningson, D. S. 1992 A new mechanism for rapid transition involving a pair of oblique waves. Phys. Fluids A 4 (9), 1986–1989.CrossRefGoogle Scholar
Schneider, S. P. 2004 Hypersonic laminar-turbulent transition on circular cones and scramjet forebodies. Prog. Aerosp. Sci. 40, 1–50.CrossRefGoogle Scholar
Sharma, S., Shadloo, M. S., Hadjadj, A. & Kloker, M. J. 2019 Control of oblique-type breakdown in a supersonic boundary layer employing streaks. J. Fluid Mech. 873, 1072–1089.CrossRefGoogle Scholar
Siconolfi, L., Camarri, S. & Fransson, J. H. M. 2015 Boundary layer stabilization using free-stream vortices. J. Fluid Mech. 764, R2.CrossRefGoogle Scholar
Sivasubramanian, J. & Fasel, H. F.2013 Direct numerical simulation of controlled transition in a boundary layer on a sharp cone at Mach 6. AIAA Paper 2013-0263.CrossRefGoogle Scholar
Stetson, K. F.1983 Nosetip bluntness effects on cone frustum boundary layer transition in hypersonic flow. AIAA Paper 83-1763.CrossRefGoogle Scholar
Thumm, A.1991 Numerische untersuchungen zum laminar-turbulenten strömungsumschlag in transsonischen grenzschichtströmungen. PhD thesis, Universität Stuttgart.Google Scholar
van Driest, E. R. 1956 The problem of aerodynamic heating. Aeronaut. Engng Rev. 15, 26–41.Google Scholar
Wright, M. J., Candler, G. V. & Bose, D. 1998 Data-parallel line relaxation method for the Navier–Stokes equations. AIAA J. 36 (9), 1603–1609.CrossRefGoogle Scholar
Wu, M. & Martin, M. P. 2007 Direct numerical simulation of supersonic boundary layer over a compression ramp. AIAA J. 45 (4), 879–889.CrossRefGoogle Scholar
Zanchetta, M.1996 Kinetic heating and transition studies and hypersonic speeds. PhD thesis, Imperial College of Science, Technology and Medicine, London.Google Scholar