Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T01:38:17.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Microstructural theory and the rheology of concentrated colloidal suspensions

Published online by Cambridge University Press:  03 December 2012

Ehssan Nazockdast  and
Jeffrey F. Morris
Ehssan Nazockdast
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, City University of New York, NY 10031, USA
Jeffrey F. Morris*
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, City University of New York, NY 10031, USA
*
†Email address for correspondence: morris@ccny.cuny.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A theory for the analytical prediction of microstructure of concentrated Brownian suspensions of spheres in simple-shear flow is developed. The computed microstructure is used in a prediction of the suspension rheology. A near-hard-sphere suspension is studied for solid volume fraction $\phi \leq 0. 55$ and Péclet number 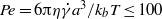$Pe= 6\lrm{\pi} \eta \dot {\gamma } {a}^{3} / {k}_{b} T\leq 100$; $a$ is the particle radius, $\eta $ is the suspending Newtonian fluid viscosity, 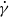$\dot {\gamma } $ is the shear rate, 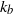${k}_{b} $ is the Boltzmann constant and 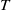$T$ is absolute temperature. The method developed determines the steady pair distribution function 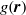$g(\mathbi{r})$, where $\mathbi{r}$ is the pair separation vector, from a solution of the Smoluchowski equation (SE) reduced to pair level. To account for the influence of the surrounding bath of particles on the interaction of a pair, an integro-differential form of the pair SE is developed; the integral portion represents the forces due to the bath which drive the pair interaction. Hydrodynamic interactions are accounted for in a pairwise fashion, based on the dominant influence of pair lubrication interactions for concentrated suspensions. The SE is modified to include the influence of shear-induced relative diffusion, and this is found to be crucial for success of the theory; a simple model based on understanding of the shear-induced self-diffusivity is used for this property. The computation of the microstructure is split into two parts, one specific to near-equilibrium (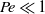$Pe\ll 1$), where a regular perturbation expansion of $g$ in 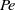$Pe$ is applied, and a general-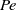$Pe$ solution of the full SE. The predicted microstructure at low 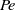$Pe$ agrees with prior theory for dilute conditions, and becomes increasingly distorted from the equilibrium isotropic state as 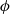$\phi $ increases at fixed 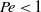$Pe\lt 1$. Normal stress differences are predicted and the zero-shear viscosity predicted agrees with simulation results obtained using a Green–Kubo formulation (Foss & Brady, J. Fluid Mech., vol. 407, 2000, pp. 167–200). At 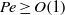$Pe\geq O(1)$, the influence of convection results in a progressively more anisotropic microstructure, with the contact values increasing with 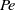$Pe$ to yield a boundary layer and a wake. Agreement of the predicted microstructure with observations from simulations is generally good and discrepancies are clearly noted. The predicted rheology captures shear thinning and shear thickening as well as normal stress differences in good agreement with simulation; quantitative agreement is best at large 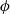$\phi $.

JFM classification

Complex Fluids: Colloids Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 420 - 452
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, M. J. & Tildesley, D. J. 1989 Computer Simulation of Liquids. Oxford University Press.Google Scholar
Ball, R. C. & Melrose, J. R. 1995 Lubrication breakdown in hydrodynamic simulations of concentrated colloids. Adv. Colloid Interface Sci. 59, 19–30.Google Scholar
Banchio, A. J. & Brady, J. F. 2003 Accelerated Stokesian dynamics: Brownian motion. J. Chem. Phys. 118, 10323–10332.CrossRefGoogle Scholar
Barnes, H. A. 1989 Shear-thickening (‘dilatancy’) in suspensions of nonaggregating solid particles dispersed in Newtonian liquids. J. Rheol. 33, 329–366.Google Scholar
Batchelor, G. K. 1977 The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 83, 97–117.Google Scholar
Batchelor, G. K. & Green, J. T. 1972a The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56, 375–400.Google Scholar
Batchelor, G. K. & Green, J. T. 1972b The determination of the bulk stress in a suspension of spherical particles to order ${c}^{2} $ . J. Fluid Mech. 56, 401–427.CrossRefGoogle Scholar
Bergenholtz, J., Brady, J. F. & Vicic, M. 2002 The non-Newtonian rheology of dilute colloidal suspensions. J. Fluid Mech. 456, 239–275.Google Scholar
Brady, J. F. 1993 The rheological behaviour of concentrated colloidal dispersions. J. Chem. Phys. 99, 567–581.CrossRefGoogle Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.Google Scholar
Brady, J. F. & Vicic, M. 1995 Normal stresses in colloidal dispersions. J. Rheol. 39, 545–566.CrossRefGoogle Scholar
Chen, L. B., Zukoski, C. F. & Ackerson, B. J. 1994 Rheological consequences of microstructural transitions in colloidal crystals. J. Rheol. 38, 193–216.CrossRefGoogle Scholar
Foss, D. R. & Brady, J. F. 1999 Self-diffusion in sheared suspensions by dynamic simulation. J. Fluid Mech. 401, 243–274.Google Scholar
Foss, D. R. & Brady, J. F. 2000 Structure, diffusion and rheology of Brownian suspensions by Stokesian dynamics simulation. J. Fluid Mech. 407, 167–200.Google Scholar
Frank, M., Anderson, D., Weeks, E. A. & Morris, J. F. 2003 Particle migration in pressure-driven flow of a Brownian suspension. J. Fluid Mech. 493, 363–378.Google Scholar
Fuchs, M. & Cates, M. E. 2009 A mode coupling theory for Brownian particles in homogeneous steady shear flow. J. Rheol. 53, 957–1000.Google Scholar
Gao, C., Kulkarni, S. D., Morris, J. F. & Gilchrist, J. F. 2010 Direct investigation of anisotropic suspension structure in pressure-driven flow. Phys. Rev. E 81, 041403.Google Scholar
Hansen, J.-P. & McDonald, I. R. 1986 Theory of Simple Liquids, 3rd edn. Elsevier.Google Scholar
Kim, S. & Karrila, S. 2005 Microhydrodynamics: Principles and Selected Applications, 1st edn. Dover.Google Scholar
Kulkarni, S. D. & Morris, J. F. 2009 Ordering transition and structural evolution under shear in Brownian suspensions. J. Rheol. 53, 417–439.Google Scholar
Leighton, D. T. & Acrivos, A. 1987a Measurement of shear-induced self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.CrossRefGoogle Scholar
Leighton, D. T. & Acrivos, A. 1987b The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Lionberger, R. A. & Russel, W. B. 1997 A Smoluchowski theory with simple approximations for hydrodynamic interactions in concentrated dispersions. J. Rheol. 41, 399–425.Google Scholar
Mazur, P. & Van Saarloos, W. 1982 Many-sphere hydrodynamic interactions and mobilities in a suspension. Physica A 115, 21–57.CrossRefGoogle Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J. Rheol. 43, 1213–1237.CrossRefGoogle Scholar
Morris, J. F. & Brady, J. F. 1996 Self-diffusion in sheared suspensions. J. Fluid Mech. 312, 223–252.Google Scholar
Morris, J. F. & Katyal, B. 2002 Microstructure from simulated Brownian suspension flows at large shear rate. Phys. Fluids 14, 1920–1937.Google Scholar
Nazockdast, E. & Morris, J. F. 2012 Effect of repulsive interactions on structure and rheology of sheared colloidal dispersions. Soft Matt. 8, 4223–4234.CrossRefGoogle Scholar
Rice, S. A. & Lekner, J. 1965 On the equation of state of the rigid-sphere fluid. J. Chem. Phys. 42, 3559–3565.Google Scholar
Russel, W. B., Saville, D. A. & Schowalter, W. R. 1995 Colloidal Dispersions. Cambridge University Press.Google Scholar
Sierou, A. & Brady, J. F. 2001 Accelerated Stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.Google Scholar
Sierou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 46, 1031–1056.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.CrossRefGoogle Scholar
Szamel, G. 2001 Nonequilibrium structure and rheology of concentrated colloidal suspensions: linear response. J. Chem. Phys. 114, 8708–8717.Google Scholar
Throop, G. & Bearman, R. 1965 Numerical solutions of the Percus–Yevick equation for the hard-sphere potential. J. Chem. Phys. 42, 2408–2411.Google Scholar
Vermant, J. & Solomon, M. J. 2005 Flow-induced structure in colloidal suspensions. J. Phys.: Condens. Matter 17 (4), R187–R216.Google Scholar
Wagner, N. J. & Ackerson, B. J. 1992 Analysis of nonequilibrium structures of shearing colloidal suspensions. J. Chem. Phys. 97, 1473–1484.Google Scholar
van der Werff, J. C. & de Kruif, C. G. 1989 Hard-sphere colloidal dispersions: the scaling of rheological properties with particle size, volume fraction, and shear rate. J. Rheol. 33, 421–454.Google Scholar
Yurkovetsky, Y. & Morris, J. F. 2006 Triplet correlation in sheared suspensions of Brownian particles. J. Chem. Phys. 124, 204908–204919.Google Scholar
Yurkovetsky, Y. & Morris, J. F. 2008 Particle pressure in sheared Brownian suspensions. J. Rheol. 52, 141–164.Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185–220.Google Scholar