Article contents
Modal stability analysis of a helical vortex tube with axial flow
Published online by Cambridge University Press: 05 December 2013
Abstract
The linear stability of a helical vortex tube with axial flow, which is a model of helical vortices emanating from rotating wings, is studied by modal stability analysis. At the leading order the base flow is set to the Rankine vortex with uniform velocity along the helical tube whose centreline is a helix of constant curvature and torsion. The helical vortex tube in an infinite domain, in which the free boundary condition is imposed at the surface of the tube, is our major target although the case of the rigid boundary condition is also considered in order to elucidate the effects of torsion and the combined effects of torsion and axial flow. The analysis is based on the linearized incompressible Euler equations expanded in  $\epsilon $ which is the ratio of the core to curvature radius of the tube. The unstable growth rate can be evaluated using the leading-order neutral modes called the Kelvin waves with the expanded equations. At
$\epsilon $ which is the ratio of the core to curvature radius of the tube. The unstable growth rate can be evaluated using the leading-order neutral modes called the Kelvin waves with the expanded equations. At 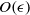 $O(\epsilon )$ the instability is a linear combination of the curvature instability due to the curvature of the tube and the precessional instability due to the axial flow, both parametric instabilities appearing at the same resonance condition. At the next order
$O(\epsilon )$ the instability is a linear combination of the curvature instability due to the curvature of the tube and the precessional instability due to the axial flow, both parametric instabilities appearing at the same resonance condition. At the next order 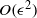 $O({\epsilon }^{2} )$ not only the effects of torsion but also the combined effects of torsion and axial flow appear, a fact which has been shown only for the short-wave limit. The maximum growth rate increases for the right-handed/left-handed helix with positive/negative helicity, in which the torsion makes the period of particle motion increase. All results converge to the previous local stability results in the short-wave limit. The differences between the two cases of different boundary conditions are due to the isolated mode of the free boundary case, whose dispersion curve depends strongly on the axial flow.
$O({\epsilon }^{2} )$ not only the effects of torsion but also the combined effects of torsion and axial flow appear, a fact which has been shown only for the short-wave limit. The maximum growth rate increases for the right-handed/left-handed helix with positive/negative helicity, in which the torsion makes the period of particle motion increase. All results converge to the previous local stability results in the short-wave limit. The differences between the two cases of different boundary conditions are due to the isolated mode of the free boundary case, whose dispersion curve depends strongly on the axial flow.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 23
- Cited by


