Article contents
A model for the constant-density boundary layer surrounding fire whirls
Published online by Cambridge University Press: 06 August 2020
Abstract
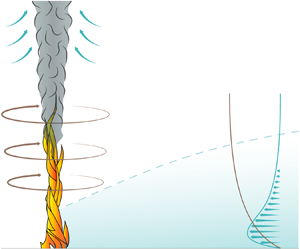
This paper investigates the steady axisymmetric structure of the cold boundary-layer flow surrounding fire whirls developing over localized fuel sources lying on a horizontal surface. The inviscid swirling motion found outside the boundary layer, driven by the entrainment of the buoyant turbulent plume of hot combustion products that develops above the fire, is described by an irrotational solution, obtained by combining Taylor's self-similar solution for the motion in the axial plane with the azimuthal motion induced by a line vortex of circulation  $2 {\rm \pi}\Gamma$. The development of the boundary layer from a prescribed radial location is determined by numerical integration for different swirl levels, measured by the value of the radial-to-azimuthal velocity ratio
$2 {\rm \pi}\Gamma$. The development of the boundary layer from a prescribed radial location is determined by numerical integration for different swirl levels, measured by the value of the radial-to-azimuthal velocity ratio  $\sigma$ at the initial radial location. As in the case
$\sigma$ at the initial radial location. As in the case  $\sigma =0$, treated in the seminal boundary-layer analysis of Burggraf et al. (Phys. Fluids, vol. 14, 1971, pp. 1821–1833), the pressure gradient associated with the centripetal acceleration of the inviscid flow is seen to generate a pronounced radial inflow. Specific attention is given to the terminal shape of the boundary-layer velocity near the axis, which displays a three-layered structure that is described by matched asymptotic expansions. The resulting composite expansion, dependent on the level of ambient swirl through the parameter
$\sigma =0$, treated in the seminal boundary-layer analysis of Burggraf et al. (Phys. Fluids, vol. 14, 1971, pp. 1821–1833), the pressure gradient associated with the centripetal acceleration of the inviscid flow is seen to generate a pronounced radial inflow. Specific attention is given to the terminal shape of the boundary-layer velocity near the axis, which displays a three-layered structure that is described by matched asymptotic expansions. The resulting composite expansion, dependent on the level of ambient swirl through the parameter  $\sigma$, is employed as boundary condition to describe the deflection of the boundary-layer flow near the axis to form a vertical swirl jet. Numerical solutions of the resulting non-slender collision region for different values of
$\sigma$, is employed as boundary condition to describe the deflection of the boundary-layer flow near the axis to form a vertical swirl jet. Numerical solutions of the resulting non-slender collision region for different values of  $\sigma$ are presented both for inviscid flow and for viscous flow with moderately large values of the controlling Reynolds number
$\sigma$ are presented both for inviscid flow and for viscous flow with moderately large values of the controlling Reynolds number  $\Gamma /\nu$. The velocity description provided is useful in mathematical formulations of localized fire-whirl flows, providing consistent boundary conditions accounting for the ambient swirl level.
$\Gamma /\nu$. The velocity description provided is useful in mathematical formulations of localized fire-whirl flows, providing consistent boundary conditions accounting for the ambient swirl level.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
Present address: Department of Aerospace Engineering, Auburn University, Auburn, USA.
References
REFERENCES
- 6
- Cited by

