Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Scarpellini, Alessandro
Finazzi, Valentina
Schito, Paolo
Bionda, Arianna
Ratti, Andrea
and
Demir, Ali Gökhan
2021.
Laser Powder Bed Fusion of a Topology Optimized and Surface Textured Rudder Bulb with Lightweight and Drag-Reducing Design.
Journal of Marine Science and Engineering,
Vol. 9,
Issue. 9,
p.
1032.
Zare, Armin
2021.
Data-enhanced Kalman filtering of colored process noise.
p.
6603.
Hewawaduge, Dhanushki
Summers, Tyler
and
Zare, Armin
2021.
Robustness of variance suppression in channel flows with imperfect transverse wall oscillations.
p.
292.
Yang, Chenghao
Feng, Heying
Peng, Yehui
Tong, Fan
and
Bao, Nvzi
2022.
Numerical investigation of rod–airfoil interaction noise reduction using cylindrical collars.
The Journal of the Acoustical Society of America,
Vol. 151,
Issue. 6,
p.
3641.
Yang, Chenghao
Feng, Heying
Peng, Yehui
and
Bao, Nvzi
2022.
Proceedings of the 5th China Aeronautical Science and Technology Conference.
Vol. 821,
Issue. ,
p.
62.
Tian, Guizhong
Zhang, Yaosheng
Feng, Xiaoming
and
Hu, Yushen
2022.
Focus on Bioinspired Textured Surfaces toward Fluid Drag Reduction: Recent Progresses and Challenges.
Advanced Engineering Materials,
Vol. 24,
Issue. 1,
Liu, Min
and
Ma, Liran
2022.
Drag reduction methods at solid-liquid interfaces.
Friction,
Vol. 10,
Issue. 4,
p.
491.
Zong, H.
Su, Z.
Liang, H.
and
Wu, Y.
2022.
Experimental investigation and reduced-order modeling of plasma jets in a turbulent boundary layer for skin-friction drag reduction.
Physics of Fluids,
Vol. 34,
Issue. 8,
Fan, Yitong
Atzori, Marco
Vinuesa, Ricardo
Gatti, Davide
Schlatter, Philipp
and
Li, Weipeng
2022.
Decomposition of the mean friction drag on an NACA4412 airfoil under uniform blowing/suction.
Journal of Fluid Mechanics,
Vol. 932,
Issue. ,
ZHENG, Borui
JIN, Yuanzhong
YU, Minghao
LI, Yueqiang
WU, Bin
and
CHEN, Quanlong
2022.
Turbulent drag reduction by spanwise slot blowing pulsed plasma actuation.
Plasma Science and Technology,
Vol. 24,
Issue. 11,
p.
114003.
Li, Zhiping
He, Long
and
Zheng, Yixuan
2022.
Quasi-Analytical Solution of Optimum and Maximum Depth of Transverse V-Groove for Drag Reduction at Different Reynolds Numbers.
Symmetry,
Vol. 14,
Issue. 2,
p.
342.
Heyat Davoudian, Salar
and
Javadi, Khodayar
2022.
Flexible polymeric tail for micro robot drag reduction bioinspired by the nature microorganisms.
Physics of Fluids,
Vol. 34,
Issue. 11,
Habibi Khorasani, Seyed Morteza
Lācis, Uǧis
Pasche, Simon
Rosti, Marco Edoardo
and
Bagheri, Shervin
2022.
Near-wall turbulence alteration with the transpiration-resistance model.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Hewawaduge, Dhanushki
and
Zare, Armin
2022.
Input-output analysis of stochastic base flow uncertainty.
Physical Review Fluids,
Vol. 7,
Issue. 7,
Du, Zengzhi
Li, Hongyuan
Cao, Yufan
Wan, Xia
Xiang, Yaolei
Lv, Pengyu
and
Duan, Huiling
2022.
Control of flow separation using biomimetic shark scales with fixed tilt angles.
Experiments in Fluids,
Vol. 63,
Issue. 10,
Endrikat, S.
Newton, R.
Modesti, D.
García-Mayoral, R.
Hutchins, N.
and
Chung, D.
2022.
Reorganisation of turbulence by large and spanwise-varying riblets.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Padovan, Alberto
and
Rowley, Clarence W.
2022.
Analysis of the dynamics of subharmonic flow structures via the harmonic resolvent: Application to vortex pairing in an axisymmetric jet.
Physical Review Fluids,
Vol. 7,
Issue. 7,
Scarpellini, Alessandro
Schito, Paolo
and
Demir, Ali Gökhan
2023.
Feasibility of using bio-mimicking fish scale textures in LPBF for water drag-reducing surfaces.
Progress in Additive Manufacturing,
Vol. 8,
Issue. 6,
p.
1209.
Chen, Xianliang
Cheng, Cheng
Gan, Jianping
and
Fu, Lin
2023.
Study of the linear models in estimating coherent velocity and temperature structures for compressible turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 973,
Issue. ,
Pakatchian, Mohammad Reza
Rocha, Joana
and
Li, Lucy
2023.
Advances in Riblets Design.
Applied Sciences,
Vol. 13,
Issue. 19,
p.
10893.
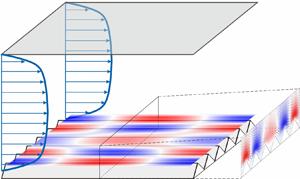
 $10\,\%$, but their systematic design remains an open challenge. In this paper we develop a model-based framework to quantify the effect of streamwise-aligned spanwise-periodic riblets on kinetic energy and skin-friction drag in turbulent channel flow. We model the effect of riblets as a volume penalization in the Navier–Stokes equations and use the statistical response of the eddy-viscosity-enhanced linearized equations to quantify the effect of background turbulence on the mean velocity and skin-friction drag. For triangular riblets, our simulation-free approach reliably predicts drag-reducing trends as well as mechanisms that lead to performance deterioration for large riblets. We investigate the effect of height and spacing on drag reduction and demonstrate a correlation between energy suppression and drag reduction for appropriately sized riblets. We also analyse the effect of riblets on drag-reduction mechanisms and turbulent flow structures including very large-scale motions. Our results demonstrate the utility of our approach in capturing the effect of riblets on turbulent flows using models that are tractable for analysis and optimization.
$10\,\%$, but their systematic design remains an open challenge. In this paper we develop a model-based framework to quantify the effect of streamwise-aligned spanwise-periodic riblets on kinetic energy and skin-friction drag in turbulent channel flow. We model the effect of riblets as a volume penalization in the Navier–Stokes equations and use the statistical response of the eddy-viscosity-enhanced linearized equations to quantify the effect of background turbulence on the mean velocity and skin-friction drag. For triangular riblets, our simulation-free approach reliably predicts drag-reducing trends as well as mechanisms that lead to performance deterioration for large riblets. We investigate the effect of height and spacing on drag reduction and demonstrate a correlation between energy suppression and drag reduction for appropriately sized riblets. We also analyse the effect of riblets on drag-reduction mechanisms and turbulent flow structures including very large-scale motions. Our results demonstrate the utility of our approach in capturing the effect of riblets on turbulent flows using models that are tractable for analysis and optimization.

