Published online by Cambridge University Press: 12 December 2023
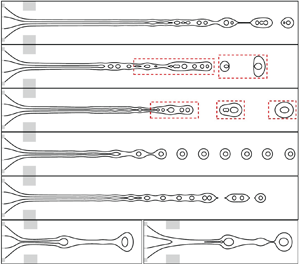
The breakup of coaxial cone-jet interfaces to compound droplets in axisymmetric co-flow focusing (CFF) upon actuation is studied through numerical simulations. Due to the coupling effect of double interfaces, the response behaviours of coaxial cone-jet flow to actuation are more complex than those of a single-layered interface structure. Particularly, the coaxial jet presents totally different response modes between weak and strong interface coupling situations. In this work, the phase diagrams of response modes for coaxial jet breakup are depicted, considering the effect of perturbation frequency, amplitude and liquid flow rates. In particular, the breakup of a coaxial jet can be synchronized with actuation within a frequency range containing the natural breakup frequency, resulting in uniform compound droplets with a single core inside the shell, and the size of droplets can be adjusted by frequency. As the perturbation frequency exceeds the upper critical value, the external perturbation is unable to dominate the jet breakup, while below the lower critical frequency, the jet breaks up with multiple droplets generated in one period. The perturbation amplitude mainly affects the jet breakup length and also leads to the transition between different response modes. The coaxial cone upstream of the orifice can act as a buffer layer, regulating the perturbation amplitude of the coaxial jet downstream. The degree of buffering effect is affected by the perturbation frequency and amplitude. As the perturbation amplitude approaches unity, the decrease of perturbation frequency leads to the intermittent jet behaviour from the cone tip with a vibrating manner of the coaxial cone. Based on the linear instability analysis on the simplified single jet models for weak-coupled and strong-coupled jets, scaling analyses are carried out, which predict the jet breakup length and the natural frequency and critical frequency for the synchronized breakup. Finally, a strong pulse is added on the perturbation to produce compound droplets with a controllable number of cores. The present work provides valuable guidance for the practical application of on-demand compound droplet generation through active CFF.