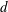Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T01:25:07.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Moment theories for a $d$-dimensional dilute granular gas of Maxwell molecules

Published online by Cambridge University Press:  06 February 2020

Vinay Kumar Gupta Open the ORCID record for Vinay Kumar Gupta [Opens in a new window]
Vinay Kumar Gupta*
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Indore, Indore453552, India Mathematics Institute, University of Warwick, CoventryCV4 7AL, UK
*
†Email address for correspondence: vkg@iiti.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

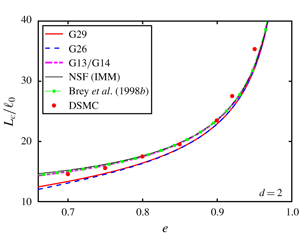
Various systems of moment equations – consisting of up to $(d+3)(d^{2}+6d+2)/6$ moments – in a general dimension $d$ for a dilute granular gas composed of Maxwell molecules are derived from the inelastic Boltzmann equation by employing the Grad moment method. The Navier–Stokes-level constitutive relations for the stress and heat flux appearing in the system of mass, momentum and energy balance equations are determined from the derived moment equations. It has been shown that the moment equations only for the hydrodynamic field variables (density, velocity and granular temperature), stress and heat flux – along with the time-independent value of the fourth cumulant – are sufficient for determining the Navier–Stokes-level constitutive relations in the case of inelastic Maxwell molecules, and that the other higher-order moment equations do not play any role in this case. The homogeneous cooling state of a freely cooling granular gas is investigated with the system of the Grad $(d+3)(d^{2}+6d+2)/6$-moment equations and its various subsystems. By performing a linear stability analysis in the vicinity of the homogeneous cooling state, the critical system size for the onset of instability is estimated through the considered Grad moment systems. The results on critical system size from the presented moment theories are found to be in reasonably good agreement with those from simulations.

JFM classification

Granular media: Granular media Rarefied Gas Flow: Kinetic theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A12
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M., Chikkadi, V. & Gupta, V. K. 2009 Density waves and the effect of wall roughness in granular Poiseuille flow: simulation and linear stability. Eur. Phys. J. ST 179, 69–90.CrossRefGoogle Scholar
Ben-Naim, E. & Krapivsky, P. L. 2000 Multiscaling in inelastic collisions. Phys. Rev. E 61, R5–R8.CrossRefGoogle ScholarPubMed
Ben-Naim, E. & Krapivsky, P. L. 2002 Scaling, multiscaling, and nontrivial exponents in inelastic collision processes. Phys. Rev. E 66, 011309.CrossRefGoogle ScholarPubMed
Bisi, M., Spiga, G. & Toscani, G. 2004 Grad’s equations and hydrodynamics for weakly inelastic granular flows. Phys. Fluids 16, 4235–4247.CrossRefGoogle Scholar
Bobylev, A. V. 1982 The Chapman–Enskog and Grad methods for solving the Boltzmann equation. Sov. Phys. Dokl. 27, 29–31.Google Scholar
Brey, J. J., Dufty, J. W., Kim, C. S. & Santos, A. 1998a Hydrodynamics for granular flow at low density. Phys. Rev. E 58, 4638–4653.CrossRefGoogle Scholar
Brey, J. J., Dufty, J. W. & Santos, A. 1997 Dissipative dynamics for hard spheres. J. Stat. Phys. 87, 1051–1066.CrossRefGoogle Scholar
Brey, J. J., García de Soria, M. I. & Maynar, P. 2010 Breakdown of hydrodynamics in the inelastic Maxwell model of granular gases. Phys. Rev. E 82, 021303.CrossRefGoogle ScholarPubMed
Brey, J. J. & Ruiz-Montero, M. J. 2004 Simulation study of the Green–Kubo relations for dilute granular gases. Phys. Rev. E 70, 051301.CrossRefGoogle ScholarPubMed
Brey, J. J., Ruiz-Montero, M. J. & Cubero, D. 1999 Origin of density clustering in a freely evolving granular gas. Phys. Rev. E 60, 3150–3157.CrossRefGoogle Scholar
Brey, J. J., Ruiz-Montero, M. J., Maynar, P. & García de Soria, M. I. 2005 Hydrodynamic modes, Green–Kubo relations, and velocity correlations in dilute granular gases. J. Phys.: Condens. Matter 17, S2489–S2502.Google Scholar
Brey, J. J., Ruiz-Montero, M. J. & Moreno, F. 1998b Instability and spatial correlations in a dilute granular gas. Phys. Fluids 10, 2976–2982.CrossRefGoogle Scholar
Brilliantov, N. V., Formella, A. & Pöschel, T. 2018 Increasing temperature of cooling granular gases. Nat. Commun. 9, 797.CrossRefGoogle ScholarPubMed
Brilliantov, N. V. & Pöschel, T. 2004 Kinetic Theory of Granular Gases. Oxford University Press.CrossRefGoogle Scholar
Cai, Z., Fan, Y. & Li, R. 2013 Globally hyperbolic regularization of Grad’s moment system in one-dimensional space. Commun. Math. Sci. 11, 547–571.CrossRefGoogle Scholar
Cai, Z., Fan, Y. & Li, R. 2014a Globally hyperbolic regularization of Grad’s moment system. Commun. Pure Appl. Maths 67, 464–518.CrossRefGoogle Scholar
Cai, Z., Fan, Y. & Li, R. 2014b On hyperbolicity of 13-moment system. Kinet. Relat. Models 7, 415–432.CrossRefGoogle Scholar
Cai, Z. & Li, R. 2010 Numerical regularized moment method of arbitrary order for Boltzmann-BGK equation. SIAM J. Sci. Comput. 32, 2875–2907.CrossRefGoogle Scholar
Campbell, C. S. 1990 Rapid granular flows. Annu. Rev. Fluid Mech. 22, 57–90.CrossRefGoogle Scholar
Carrillo, J. A., Cercignani, C. & Gamba, I. M. 2000 Steady states of a Boltzmann equation for driven granular media. Phys. Rev. E 62, 7700–7707.CrossRefGoogle ScholarPubMed
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-Uniform Gases. Cambridge University Press.Google Scholar
Claydon, R., Shrestha, A., Rana, A. S., Sprittles, J. E. & Lockerby, D. A. 2017 Fundamental solutions to the regularised 13-moment equations: efficient computation of three-dimensional kinetic effects. J. Fluid Mech. 833, R4.CrossRefGoogle Scholar
Ernst, M. H. & Brito, R. 2002 Scaling solutions of inelastic Boltzmann equations with over-populated high energy tails. J. Stat. Phys. 109, 407–432.CrossRefGoogle Scholar
Fan, Y., Koellermeier, J., Li, J., Li, R. & Torrilhon, M. 2016 Model reduction of kinetic equations by operator projection. J. Stat. Phys. 162, 457–486.CrossRefGoogle Scholar
Garzó, V. 2005 Instabilities in a free granular fluid described by the Enskog equation. Phys. Rev. E 72, 021106.CrossRefGoogle Scholar
Garzó, V. 2013 Grad’s moment method for a granular fluid at moderate densities: Navier–Stokes transport coefficients. Phys. Fluids 25, 043301.CrossRefGoogle Scholar
Garzó, V. 2019 Granular Gaseous Flows. Springer Nature.CrossRefGoogle Scholar
Garzó, V. & Dufty, J. W. 1999 Dense fluid transport for inelastic hard spheres. Phys. Rev. E 59, 5895–5911.CrossRefGoogle ScholarPubMed
Garzó, V. & Santos, A. 2003 Kinetic Theory of Gases in Shear Flows. Nonlinear Transport. Kluwer.CrossRefGoogle Scholar
Garzó, V. & Santos, A. 2007 Third and fourth degree collisional moments for inelastic Maxwell models. J. Phys. A: Math. Theor. 40, 14927–14943.CrossRefGoogle Scholar
Garzó, V. & Santos, A. 2011 Hydrodynamics of inelastic Maxwell models. Math. Model. Nat. Phenom. 6, 37–76.CrossRefGoogle Scholar
Garzó, V., Santos, A. & Montanero, J. M. 2007 Modified Sonine approximation for the Navier–Stokes transport coefficients of a granular gas. Physica A 376, 94–107.CrossRefGoogle Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.CrossRefGoogle Scholar
Goldshtein, A. & Shapiro, M. 1995 Mechanics of collisional motion of granular materials. Part 1. General hydrodynamic equations. J. Fluid Mech. 282, 75–114.CrossRefGoogle Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2, 331–407.CrossRefGoogle Scholar
Gu, X.-J. & Emerson, D. R. 2007 A computational strategy for the regularized 13 moment equations with enhanced wall-boundary conditions. J. Comput. Phys. 225, 263–283.CrossRefGoogle Scholar
Gu, X.-J. & Emerson, D. R. 2009 A high-order moment approach for capturing non-equilibrium phenomena in the transition regime. J. Fluid Mech. 636, 177–216.CrossRefGoogle Scholar
Gupta, V. K.2011 Kinetic theory and Burnett order constitutive relations for a smooth granular gas. Master’s thesis, JNCASR, Bangalore, India.Google Scholar
Gupta, V. K.2015 Mathematical modeling of rarefied gas mixtures. PhD thesis, RWTH Aachen University, Germany.Google Scholar
Gupta, V. K. & Shukla, P. 2017 Grad-type fourteen-moment theory for dilute granular gases. In Indian Academy of Sciences Conference Series, vol. 1, pp. 133–143.Google Scholar
Gupta, V. K., Shukla, P. & Torrilhon, M. 2018 Higher-order moment theories for dilute granular gases of smooth hard spheres. J. Fluid Mech. 836, 451–501.CrossRefGoogle Scholar
Gupta, V. K., Struchtrup, H. & Torrilhon, M. 2016 Regularized moment equations for binary gas mixtures: derivation and linear analysis. Phys. Fluids 28, 042003.CrossRefGoogle Scholar
Gupta, V. K. & Torrilhon, M. 2012 Automated Boltzmann collision integrals for moment equations. AIP Conf. Proc. 1501, 67–74.CrossRefGoogle Scholar
Gupta, V. K. & Torrilhon, M. 2015 Higher order moment equations for rarefied gas mixtures. Proc. R. Soc. Lond. A 471, 20140754.CrossRefGoogle Scholar
Haff, P. K. 1983 Grain flow as a fluid-mechanical phenomenon. J. Fluid Mech. 134, 401–430.CrossRefGoogle Scholar
Jenkins, J. T. & Richman, M. W. 1985a Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.CrossRefGoogle Scholar
Jenkins, J. T. & Richman, M. W. 1985b Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28, 3485–3494.CrossRefGoogle Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 130, 187–202.CrossRefGoogle Scholar
Junk, M. 1998 Domain of definition of Levermore’s five-moment system. J. Stat. Phys. 93, 1143–1167.CrossRefGoogle Scholar
Junk, M. & Unterreiter, A. 2002 Maximum entropy moment systems and Galilean invariance. Contin. Mech. Thermodyn. 14, 563–576.CrossRefGoogle Scholar
Khalil, N., Garzó, V. & Santos, A. 2014 Hydrodynamic Burnett equations for inelastic Maxwell models of granular gases. Phys. Rev. E 89, 052201.CrossRefGoogle ScholarPubMed
Koellermeier, J., Schaerer, R. P. & Torrilhon, M. 2014 A framework for hyperbolic approximation of kinetic equations using quadrature-based projection methods. Kinet. Relat. Models 7, 531–549.CrossRefGoogle Scholar
Koellermeier, J. & Torrilhon, M. 2017 Numerical study of partially conservative moment equations in kinetic theory. Commun. Comput. Phys. 21, 981–1011.CrossRefGoogle Scholar
Koellermeier, J. & Torrilhon, M. 2018 Two-dimensional simulation of rarefied gas flows using quadrature-based moment equations. Multiscale Model. Simul. 16, 1059–1084.CrossRefGoogle Scholar
Kohlstedt, K., Snezhko, A., Sapozhnikov, M. V., Aranson, I. S., Olafsen, J. S. & Ben-Naim, E. 2005 Velocity distributions of granular gases with drag and with long-range interactions. Phys. Rev. Lett. 95, 068001.CrossRefGoogle ScholarPubMed
Kremer, G. M. 2010 An Introduction to the Boltzmann Equation and Transport Processes in Gases. Springer.CrossRefGoogle Scholar
Kremer, G. M. & Marques, W. Jr. 2011 Fourteen moment theory for granular gases. Kinet. Relat. Models 4, 317–331.CrossRefGoogle Scholar
Kremer, G. M., Santos, A. & Garzó, V. 2014 Transport coefficients of a granular gas of inelastic rough hard spheres. Phys. Rev. E 90, 022205.CrossRefGoogle ScholarPubMed
Lasanta, A., Vega Reyes, F., Prados, A. & Santos, A. 2017 When the hotter cools more quickly: Mpemba effect in granular fluids. Phys. Rev. Lett. 119, 148001.CrossRefGoogle ScholarPubMed
Levermore, C. D. 1996 Moment closure hierarchies for kinetic theories. J. Stat. Phys. 83, 1021–1065.CrossRefGoogle Scholar
Lockerby, D. A. & Collyer, B. 2016 Fundamental solutions to moment equations for the simulation of microscale gas flows. J. Fluid Mech. 806, 413–436.CrossRefGoogle Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 140, 223–256.CrossRefGoogle Scholar
Lutsko, J. F. 2005 Transport properties of dense dissipative hard-sphere fluids for arbitrary energy loss models. Phys. Rev. E 72, 021306.CrossRefGoogle ScholarPubMed
Maxwell, J. C. 1867 On the dynamical theory of gases. Phil. Trans. R. Soc. Lond. A 157, 49–88.Google Scholar
McDonald, J. & Torrilhon, M. 2013 Affordable robust moment closures for CFD based on the maximum-entropy hierarchy. J. Comput. Phys. 251, 500–523.CrossRefGoogle Scholar
Mitrano, P. P., Dahl, S. R., Cromer, D. J., Pacella, M. S. & Hrenya, C. M. 2011 Instabilities in the homogeneous cooling of a granular gas: A quantitative assessment of kinetic-theory predictions. Phys. Fluids 23, 093303.CrossRefGoogle Scholar
Montanero, J. M., Santos, A. & Garzó, V. 2005 DSMC evaluation of the Navier–Stokes shear viscosity of a granular fluid. AIP Conf. Proc. 762, 797–802.CrossRefGoogle Scholar
Montanero, J. M., Santos, A. & Garzó, V. 2007 First-order Chapman–Enskog velocity distribution function in a granular gas. Physica A 376, 75–93.CrossRefGoogle Scholar
Müller, I. & Ruggeri, T. 1998 Rational Extended Thermodynamics. Springer.CrossRefGoogle Scholar
van Noije, T. P. C. & Ernst, M. H. 1998 Velocity distributions in homogeneous granular fluids: the free and the heated case. Granul. Matt. 1, 57–64.CrossRefGoogle Scholar
Noskowicz, S. H., Bar-Lev, O., Serero, D. & Goldhirsch, I. 2007 Computer-aided kinetic theory and granular gases. Europhys. Lett. 79, 60001.CrossRefGoogle Scholar
Risso, D. & Cordero, P. 2002 Dynamics of rarefied granular gases. Phys. Rev. E 65, 021304.CrossRefGoogle ScholarPubMed
Santos, A. 2003 Transport coefficients of d-dimensional inelastic Maxwell models. Physica A 321, 442–466.CrossRefGoogle Scholar
Santos, A. 2009 Solutions of the moment hierarchy in the kinetic theory of Maxwell models. Contin. Mech. Thermodyn. 21, 361–387.CrossRefGoogle Scholar
Santos, A. & Garzó, V. 2012 Collisional rates for the inelastic Maxwell model: application to the divergence of anisotropic high-order velocity moments in the homogeneous cooling state. Granul. Matt. 14, 105–110.CrossRefGoogle Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–74.CrossRefGoogle Scholar
Shukla, P., Biswas, L. & Gupta, V. K. 2019 Shear-banding instability in arbitrarily inelastic granular shear flows. Phys. Rev. E 100, 032903.CrossRefGoogle ScholarPubMed
Struchtrup, H. 2004 Stable transport equations for rarefied gases at high orders in the Knudsen number. Phys. Fluids 16, 3921–3934.CrossRefGoogle Scholar
Struchtrup, H. 2005 Macroscopic Transport Equations for Rarefied Gas Flows. Springer.CrossRefGoogle Scholar
Struchtrup, H. & Torrilhon, M. 2003 Regularization of Grad’s 13 moment equations: derivation and linear analysis. Phys. Fluids 15, 2668–2680.CrossRefGoogle Scholar
Torrilhon, M. 2006 Two-dimensional bulk microflow simulations based on regularized Grad’s 13 moment equations. Multiscale Model. Simul. 5, 695–728.CrossRefGoogle Scholar
Torrilhon, M. 2010 Hyperbolic moment equations in kinetic gas theory based on multi-variate Pearson-IV-distributions. Commun. Comput. Phys. 7, 639–673.CrossRefGoogle Scholar
Torrilhon, M. 2015 Convergence study of moment approximations for boundary value problems of the Boltzmann-BGK equation. Commun. Comput. Phys. 18, 529–557.CrossRefGoogle Scholar
Torrilhon, M. 2016 Modeling nonequilibrium gas flow based on moment equations. Annu. Rev. Fluid Mech. 48, 429–458.CrossRefGoogle Scholar
Torrilhon, M. & Struchtrup, H. 2004 Regularized 13-moment equations: shock structure calculations and comparison to Burnett models. J. Fluid Mech. 513, 171–198.CrossRefGoogle Scholar
Torrilhon, M. & Struchtrup, H. 2008 Boundary conditions for regularized 13-moment equations for micro-channel-flows. J. Comput. Phys. 227, 1982–2011.CrossRefGoogle Scholar
Supplementary material: File

Gupta et al. supplementary material

Gupta et al. supplementary material

Download Gupta et al. supplementary material(File)
File 447.2 KB