Monopoles in a uniform zonal flow on a quasi-geostrophic 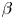$\beta $-plane: effects of the Galilean non-invariance of the rotating shallow-water equations

Abstract

Galilean non-invariance of the shallow-water equations describing the motion of a rotating fluid implies that a homogeneous background flow modifies the dynamics of localized vortices even without the $\beta $-effect. In particular, in a divergent quasi-geostrophic model on a $\beta $-plane, which originates from the shallow-water model, the equation of motion in the reference frame attached to a uniform zonal background flow has the same form as in the absence of this flow, but with a modified $\beta $-parameter depending linearly on the flow velocity $\bar{U}$. The evolution of a singular vortex (SV) embedded in such a flow consists of two stages. In the first, quasi-linear stage, the SV motion is induced by the secondary dipole ($\beta $-gyres) generated in the neighbourhood of the SV. During the next, nonlinear stage, the SV merges with the $\beta $-gyre of opposite sign to form a compact vortex pair interacting with far-field Rossby waves radiated previously by the SV, while the other $\beta $-gyre loses connection with the SV and disappears. In the absolute reference frame and with $\beta = 0$, the SV drifts downstream and at an angle to the background flow. The SV always lags behind the background flow, with the strongest resistance during the quasi-linear stage and weakening resistance at the nonlinear stage of SV evolution. In the general case where $\beta \gt 0$, the SV can move both upstream (for small-to-moderate $\bar{U} \gt 0$) and downstream (for $\bar{U} \lt 0$ or sufficiently large $\bar{U} \gt 0$). Under weak-to-moderate westward and all eastward flows the SV cyclone (anticyclone) also moves northward (southward), its meridional drift increasing with $\bar{U}$.