Morphodynamics of active nematic fluid surfaces

Abstract

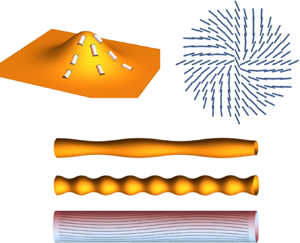
Morphodynamic equations governing the behaviour of active nematic fluids on deformable curved surfaces are constructed in the large deformation limit. Emphasis is placed on the formulation of objective rates that account for normal deformations whilst ensuring that tangential flows are Eulerian, and the use of the surface derivative (rather than the covariant derivative) in the nematic free energy, which elastically couples local order to out-of-plane bending of the surface. Focusing on surface geometry and its dynamical interplay with the hydrodynamics, several illustrative instabilities are then characterised. These include cases where the role of the Scriven–Love number and its nematic analogue are non-negligible, and where the active nematic forcing can be characterised by an analogue of the Föppl–von Kármán number. For the former, flows and changes to the nematic texture are coupled to surface geometry by viscous dissipation. This is shown to result in non-trivial relaxation dynamics for a nematic tube. For the latter, the nematic active forcing couples to the surface bending terms of the nematic free energy, resulting in extensile (active ruffling) and contractile (active pearling) instabilities in the tube shape, as well as active bend instabilities in the nematic texture. In comparison to the flat case, such bend instabilities now have a threshold set by the extrinsic curvature of the tube. Finally, we examine a topological defect located on an almost flat surface, and show that there exists a steady state where a combination of defect elasticity, activity and non-negligible spin connection drive a shape change in the surface.

1. Introduction

Two-dimensional fluid surfaces with nematic ordering are relevant for the characterisation of a variety of biological and soft matter systems, ranging from liquid crystal shells (Fernández-Nieves et al. 2007) to active composites of microtubules and kinesin motors at an oil–water interface (Sanchez et al. 2012). Of particular current interest is the increasing experimental evidence that nematic-like ordering plays a vital role in tissue mechanics (Saw et al. 2017) and morphogenesis (Maroudas-Sacks et al. 2021; Vafa & Mahadevan 2022), where the interplay between topological defects and active forces controls the morphology of protrusions and extrusions (Metselaar, Yeomans & Doostmohammadi 2019; Hoffmann et al. 2022).

Mathematically, the development of theory that couples hydrodynamics to surface geometry has led to many interesting predictions on the role of viscous forces in the ordering and shaping of membranes in both isotropic (Steigmann 1999; Hu, Zhang & Weinan 2007; Arroyo & DeSimone 2009; Rangamani et al. 2013; Sahu et al. 2020a; Tchoufag, Sahu & Mandadapu 2022) and ordered (Napoli & Vergori 2016; Nestler & Voigt 2022) fluids. Of particular note has been the inclusion of activity, leading to a variety of interesting morphodynamical phenomena and instabilities (Salbreux & Jülicher 2017; Bächer et al. 2021; Khoromskaia & Salbreux 2023; Rank & Voigt 2021; Alert 2022; Bell et al. 2022; Hoffmann et al. 2022; Nestler & Voigt 2022; Salbreux et al. 2022; Vafa & Mahadevan 2022) and even some attempts to construct rigorous shell theories of active materials (da Rocha, Bleyer & Turlier 2022). Much of this work has been driven by the desire to develop theories capable of describing the dynamics and morphogenesis of biological tissues and organisms (Jülicher, Grill & Salbreux 2018; Al-Izzi & Morris 2021).

Despite such interest, there is still a lack of formal characterisation regarding how geometry couples to dissipative and active forces in nematic fluid surfaces. To this end, we develop a closed system of dynamical equations for nematic fluid surfaces in a manner similar to the approach taken in Arroyo & DeSimone (2009) for isotropic fluid membranes. We construct normal and tangential dissipative and reactive forces for the system subject to a free energy that depends only on surface geometry, the order parameter and its derivatives. We focus specifically on nematic liquid crystals in the one-constant limit of the Frank free energy, and derive the general form of the so-called molecular field and the resulting normal forces for surfaces of arbitrary geometry (and vector ordering). Particular emphasis is placed on the formulation of objective rates that account for normal deformations whilst ensuring that tangential flows are Eulerian, and the use of the surface derivative (rather than the covariant derivative) in the nematic free energy, which elastically couples local order to out-of-plane bending of the surface. Given the increased interest in active interfaces, we also include an active $\boldsymbol{\mathsf{Q}}$-tensor term in the tangential stress tensor. From these equations, we identify and discuss three dimensionless numbers that characterise regimes where there is a non-trivial interplay between geometry, dissipation and active forces.

To highlight how these numbers govern morphodynamics, we focus on some simple concrete examples. In the first case, we consider a tube with no activity (and uniformly ordered nematic parameter as a ground state) and derive the relaxation dynamics for perturbations in the shape and order parameter. We then consider the case of active tubes, where we show that under active forces, there are three characteristic types of instability, depending on the value and sign of the activity (extensile versus contractile). Two of these instabilities are in the tube shape: contractile forces give an active pearling-like instability whose length scale is set by the bulk viscous time scale, whilst extensile forces (above a threshold) lead to a ruffling instability whose length scale is set by the active stress. In addition, we find an instability in the texture that acts to drive spontaneous bend. This occurs for extensile activity in rod-like nematics, and for contractile activity in disk-like nematics. Interestingly, although similar to known spontaneous bend instabilities in flat geometries, the effects of curvature mean that the active forcing must exceed a finite threshold even in the infinite system size. Finally, we examine steady states in shape driven by active forcing of an almost flat surface in the presence of a topological defect, and show that this leads to protrusions at the defect whose morphology is controlled by the activity. Specifically, increases in contractility lead to increased protrusion, whilst increases in extensility act to suppress protrusions.

2. A theory of deformable nematic fluid surfaces

In this section, we construct a closed system of equations for the morphodynamics of nematic fluid surfaces (figure 1). In general, certain conventions from differential geometry will be adopted, such as the use of comma ‘$,$’ and semicolon ‘$;$’ subscripts to denote partial and covariant differentiation, respectively. For the uninitiated, a brief non-rigorous introduction to such notation is given in Appendix A. For a more complete treatment, we refer the reader to Needham (2021) and/or Frankel (2011).

Figure 1. Schematic of a curved fluid surface with orientational order given by the director field $\boldsymbol {T}=T^\alpha \boldsymbol {e}_\alpha$, which moves with a velocity in $\mathbb {R}^3$ given by the vector field $\boldsymbol {V} = v^\alpha \boldsymbol {e}_\alpha +v^{(n)}\hat {\boldsymbol {n}}$.

Our starting point is a two-dimensional (2-D) Riemannian manifold $\mathcal {M}_t$, embedded in $\mathbb {R}^3$, and equipped with induced metric $g_{\alpha \beta }$ and second fundamental form $b_{\alpha \beta }$, where $\alpha, \beta \in \{1,2\}$ (and similarly for all Greek indices). The time-dependent position $\boldsymbol {R}(u^\alpha (t),t)\in \mathbb {R}^3$ of each point $u\in \mathcal {M}_t$ implies a local velocity

(2.1)\begin{equation} \frac{\mathrm{d}\boldsymbol{R}}{\mathrm{d}t}= \boldsymbol{V}=v^\alpha\boldsymbol{e}_\alpha + v^{(n)}\hat{\boldsymbol{n}}, \end{equation}

where the $\boldsymbol {e}_\alpha =\boldsymbol {R}_{,\alpha }$ are tangent to the surface at $\boldsymbol {R}$, and $\hat {\boldsymbol {n}}$ is the unit normal. To account for local order, each point is also associated with a vector $\boldsymbol {T}=T^\alpha \boldsymbol {e}_{\alpha }\in \mathcal {T}(\mathcal {M}_t)$, referred to as the director, which lives in the tangent bundle of the manifold.

Throughout, the fluid is assumed to be in the low-Reynolds-number regime, therefore inertial forces are neglected. As a result, the condition of force balance can be decomposed as

(2.2)\begin{equation} \boldsymbol{f}^e+\boldsymbol{f}^d+ \boldsymbol{f}^{bs} + \boldsymbol{f}^c + \boldsymbol{f}^a= 0, \end{equation}

where $\boldsymbol {f}^e$ are elastic forces, $\boldsymbol {f}^d$ are dissipative forces, $\boldsymbol {f}^{bs}$ are broken symmetry forces, $\boldsymbol {f}^c$ are forces from constraints, and $\boldsymbol {f}^a$ are active forces.

We will also assume that the fluid is incompressible. As a result, the only dynamical equation in our theory, in addition to the trivial (2.1), is for the director field $T^{\alpha }$ on the surface. We write this as

(2.3)\begin{equation} {D}_t T^\alpha = J^\alpha_{T} + J^\alpha_{c}, \end{equation}

where ${D}_t$ is the objective rate (calculated in § 2.2), $J^\alpha _T$ are dissipative currents resulting from an Onsager expansion/thermodynamic flux-force relation, and $J^\alpha _c$ is the current associated with the constraint of unit director magnitude.

2.1. Rate-of-deformation and vorticity tensors

A tensor of vital importance to fluid mechanics is the rate-of-deformation or strain-rate tensor $d_{\alpha \beta }$. The rate-of-deformation tensor is given by half of the time derivative of the metric on $\mathcal {M}_t$ (more formally, half of the Lie derivative with respect to the flow $\boldsymbol {V}$; Arroyo & DeSimone 2009; Marsden & Hughes 1994). If we take the time derivative of the induced metric, $g_{\alpha \beta }=\boldsymbol {e}_\alpha \boldsymbol {\cdot }\boldsymbol {e}_\beta$, as defined in (A1), then we find

(2.4)\begin{equation} \frac{\mathrm{d} g_{\alpha\beta}}{\mathrm{d}t} = \frac{\mathrm{d}\boldsymbol{e}_{\alpha}}{\mathrm{d}t}\boldsymbol{\cdot}\boldsymbol{e}_{\beta}+ \frac{\mathrm{d}\boldsymbol{e}_{\beta}}{\mathrm{d}t}\boldsymbol{\cdot}\boldsymbol{e}_{\alpha} = \boldsymbol{V}_{,\alpha}\boldsymbol{\cdot}\boldsymbol{e}_{\beta} + \boldsymbol{e}_{\alpha}\boldsymbol{\cdot}\boldsymbol{V}_{,\beta}. \end{equation}

Substituting for $\boldsymbol {V}_{,\alpha }=(v^\beta {}_{;\alpha } - v^{(n)} b^{\beta }{}_{\alpha })\boldsymbol {e}_{\beta } + (v^\beta b_{\alpha \beta } + v^{(n)}{}_{;\alpha })\hat {\boldsymbol {n}}$ (see (A13)) gives

(2.5)\begin{equation} d_{\alpha\beta}=\frac{1}{2}\,\frac{\mathrm{d} g_{\alpha\beta}}{\mathrm{d}t} = \frac{1}{2}\left(v_{\beta;\alpha} + v_{\alpha;\beta}\right) - v^{(n)} b_{\alpha\beta}. \end{equation}

Alternatively, one can start from the expression for the rate-of-deformation tensor in $\mathbb {R}^3$ and project back onto the manifold $\mathcal {M}_{t}$:

(2.6)\begin{equation} d_{\alpha\beta}\boldsymbol{e}^\alpha\otimes\boldsymbol{e}^\beta =\left[\tfrac{1}{2}\,\boldsymbol{V}_{,\alpha}\otimes\boldsymbol{e}^{\alpha} +\tfrac{1}{2}\left(\boldsymbol{V}_{,\alpha}\otimes\boldsymbol{e}^{\alpha}\right)^{\text{T}}\right]^{{\bullet}}, \end{equation}

where $({\cdot })^{\bullet }$ denotes projection onto $\mathcal {M}_t$ (i.e. contracting with tangent basis $\boldsymbol {e}_{\beta }$), which a quick calculation verifies gives the same result. Note that $\boldsymbol {V}\in \mathbb {R}^3$ but $\boldsymbol {V}$ has support only on $\mathcal {M}_t$, and that the formal derivation of this requires some subtle constructions such as extensions of vector fields (Lee 1997).

The vorticity tensor can be derived in an equivalent way, giving a result identical to that from the flat geometry version:

(2.7)\begin{equation} \varOmega_{\alpha\beta}=\tfrac{1}{2}\left(v_{\beta;\alpha}-v_{\alpha;\beta}\right), \end{equation}

which can be seen by noting that the terms of the antisymmetrised deformation tensor proportional to $b_{\alpha \beta }$ vanish by symmetry under exchange of indices of the second fundamental form.

Here, we will consider incompressible fluids, the condition for which is that the rate-of-deformation tensor is traceless:

(2.8)\begin{equation} d^\alpha{}_\alpha = \boldsymbol{\nabla}_\alpha v^\alpha - 2 H v^{(n)}=0. \end{equation}

In the absence of normal flows, this reproduces the classic incompressibility condition $\boldsymbol {\nabla }_\alpha v^\alpha =0$.

2.2. Objective rate of a vector field

The subject of objective rates is contentious in continuum mechanics, especially where changing geometry is concerned (Marsden & Hughes 1994; Nitschke & Voigt 2022). The challenge, in this case, is to ensure that tangential flows are Eulerian – i.e. coordinates are not advected with the flow – yet also properly account for out-of-plane surface dynamics, which are necessarily Lagrangian – i.e. coordinates are advected with surface movement (Waxman 1984). We adopt a pragmatic approach, and choose a projected co-rotational rate. That is, we take the co-rotational derivative in $\mathbb {R}^3$, and project down onto the surface so as to recover the co-rotational objective rates for fixed-curved and flat surfaces, while still accounting for Lagrangian deformations of the surface in the normal direction.

For a vector field $\boldsymbol {T}$, which is confined to the tangent bundle of $\mathcal {M}_{t}$ – i.e. $\boldsymbol {T}=T^\alpha \boldsymbol {e}_\alpha \in \mathcal {T}(\mathcal {M}_t)$ – this takes the form

(2.9)\begin{equation} {D}_t\boldsymbol{T}^{{\bullet}} =\left[\frac{\mathrm{d}\boldsymbol{T}}{\mathrm{d}t} + \varOmega\boldsymbol{\cdot}\boldsymbol{T}\right]^{{\bullet}} = \left[\partial_t\boldsymbol{T} +v^\alpha(\boldsymbol{T})_{,\alpha} + \varOmega\boldsymbol{\cdot}\boldsymbol{T}\right]^{{\bullet}}. \end{equation}

The first term is given by

(2.10)\begin{align} \partial_t\boldsymbol{T} &= \partial_{t}\left(T^\alpha\boldsymbol{e}_\alpha\right) = \partial_tT^\alpha \boldsymbol{e}_\alpha + T^\alpha \partial_t\boldsymbol{e}_\alpha\nonumber\\ & = \left(\partial_tT^\alpha - v^{(n)} T^\beta b_{\beta}{}^{\alpha}\right)\boldsymbol{e}_\alpha + T^\alpha v^{(n)}{}_{;\alpha} \hat{\boldsymbol{n}}, \end{align}

where we have included only contributions from changing the basis vectors due to normal velocities, since we are in an Eulerian frame tangentially and therefore tangential velocities do not advect coordinates. The second term is given by

(2.11)\begin{equation} v^{\alpha}\,\boldsymbol{\nabla}_\alpha(\boldsymbol{T}) = v^\alpha\left(T^\beta \boldsymbol{e}_\beta\right)_{,\alpha} = v^\alpha T^\beta{}_{;\alpha}\boldsymbol{e}_\beta + T^\beta v^{\alpha} b_{\alpha\beta}\hat{\boldsymbol{n}}, \end{equation}

and finally the third term is simply given by

(2.12)\begin{equation} \varOmega\boldsymbol{\cdot}\boldsymbol{T}=\varOmega^{\alpha}{}_{\beta}T^\beta\boldsymbol{e}_{\alpha}. \end{equation}

Putting this all together and projecting back onto the manifold gives

(2.13)\begin{equation} {D}_tT^\alpha = \partial_tT^\alpha + v^\beta T^\alpha{}_{;\beta} + \varOmega^{\alpha}{}_{\beta}T^\beta - v^{(n)} T^\beta b_{\beta}{}^{\alpha}, \end{equation}

which is identical to the equivalent expression in flat geometry, with the exception of the final term.

To understand the origin of this term, consider a tube in cylindrical polar coordinates that is expanding outwards with velocity $v^{(n)}=\dot {R}$, where $R$ is the radius. There is no tangential flow, and the director field is assumed to be of constant magnitude in the $\boldsymbol {e}_{\theta }$ direction (i.e. $\boldsymbol {T}=T\boldsymbol {e}_{\theta }$). In this case, the second fundamental form has one non-zero component in the $\boldsymbol {e}_\theta$ direction. As a result, as $R$ increases, so does the size of the basis vector $\boldsymbol {e}_\theta$, and we require that ${D}_tT^{\theta } = \partial _t T + \dot {R} T/R=0$ for the objective rate to be zero (fixed size for $\boldsymbol {T}$), which gives $T=T_0\exp (-\dot {R}/R)$.

2.3. Elastic forces

In general, we will consider surfaces with free energies of the form

(2.14)\begin{equation} \mathcal{F}=\int_{\mathcal{M}_t}F\left(g_{\alpha\beta},b_{\alpha\beta},T_{\alpha}\right)\mathrm{d}A, \end{equation}

where $\mathrm {d}A=\sqrt {|g|}\,\mathrm {d}\kern0.7pt x^1\,\mathrm {d}\kern0.7pt x^2$ is the area element on the manifold. Whilst other free energies fit into this class, for example the tilt field of a lipid monolayer (Selinger, MacKintosh & Schnur 1996; Terzi & Deserno 2017), we will focus on the concrete example of the free energy of a nematic liquid crystal. Here, we will make use of standard descriptions of liquid crystals to define the molecular field as

(2.15)\begin{equation} h_\alpha ={-} \frac{\delta \mathcal{F}}{\delta T^\alpha}, \end{equation}

which we will make use of in order to derive the hydrodynamics of the ordered surface. The force given by varying the surface shape is then given by

(2.16)\begin{equation} \boldsymbol{f}_{{e}}=f^\alpha_{{e}}\boldsymbol{e}_\alpha + f^{(n)}_{{e}}\hat{\boldsymbol{n}} ={-}\frac{\delta \mathcal{F}}{\delta \boldsymbol{R}}. \end{equation}

In the case of nematic liquid crystals, the one-constant approximation to the Frank free energy (Frank 1958; DeGennes & Prost 1993; Napoli & Vergori 2012, 2016) is given by

(2.17)\begin{equation} \mathcal{F}^{{LC}} = \int_{\mathcal{M}_t} \frac{\mathcal{K}}{2}\,|\tilde{\boldsymbol{\nabla}}_{s}\boldsymbol{T}|^2\,\mathrm{d}A , \end{equation}

where $\boldsymbol {T} = T^\beta \boldsymbol {e}_\beta$ is the nematic order parameter (we choose to use $T^\beta$ here rather than the usual $n^\beta$ in the nematic liquid crystal literature, in order to avoid confusion with the surface normal vector $\hat {\boldsymbol {n}}$) on the tangent bundle $\mathcal {T}(\mathcal {M}_t)$, and $\tilde {\boldsymbol {\nabla }}_s$ is the surface derivative (not the covariant derivative) (Napoli & Vergori 2012). The reason for our choice of the surface derivative, as opposed to the covariant derivative, is so as to account correctly for the bend due to extrinsic curvature. This is likely an important coupling for true active nematic surfaces, but is perhaps less relevant for nematic-like material surfaces such as epithelial tissues. The surface derivative can be written in terms of the covariant derivative and second fundamental form as

(2.18)\begin{equation} \tilde{\boldsymbol{\nabla}}_s \boldsymbol{T} = \boldsymbol{\nabla}_\alpha T^\beta \boldsymbol{e}^\alpha\otimes\boldsymbol{e}_\beta + T^\beta b_{\alpha\beta} \boldsymbol{e}^\alpha\otimes\hat{\boldsymbol{n}}, \end{equation}

thus the full free energy is given by

(2.19)\begin{equation} \mathcal{F}^{{LC}} = \int_{\mathcal{M}_t} \frac{\mathcal{K}}{2}\left[\boldsymbol{\nabla}_\alpha T^\beta\,\boldsymbol{\nabla}^\alpha T_\beta + T^\beta T_\gamma b_{\alpha\beta}b^{\alpha\gamma}\right]\mathrm{d}A. \end{equation}

We will now compute the associated functional derivatives in the free energy (${\mathcal {F}}$). The functional derivative with respect to $T^\alpha$ gives the negative of the molecular field $h_\alpha$ as

(2.20)\begin{equation} \frac{\delta \mathcal{F}^{{LC}}}{\delta T^\alpha} ={-} h_\alpha ={-}\mathcal{K} \left[ \Delta T_\alpha + \left(K\delta_\alpha^\gamma - 2H b_\alpha{}^\gamma\right)T_\gamma \right]. \end{equation}

We will make use of the rate formulas calculated in Appendix A to perform functional variations of the form

(2.21)\begin{equation} \left. \begin{aligned} \delta g_{\alpha\beta} = \delta t\,\frac{\mathrm{d}}{\mathrm{d}t}\left(g_{\alpha\beta}\right)+O(\delta t^2),\cr \delta b_{\alpha\beta} = \delta t\,\frac{\mathrm{d}}{\mathrm{d}t}\left(b_{\alpha\beta}\right)+O(\delta t^2),\cr \delta \varGamma^{\gamma}_{\alpha\beta} = \delta t\,\frac{\mathrm{d}}{\mathrm{d}t}\left(\varGamma^\gamma_{\alpha\beta}\right)+O(\delta t^2). \end{aligned} \right\} \end{equation}

Using this, we find

(2.22) $$\begin{align} \delta\mathcal{F} &= \int_{\mathcal{M}_t} \frac{\mathcal{K}}{2} \left[\vphantom{\left( T^\beta{}_{;\alpha} T_\beta{}^{;\alpha} + T^\beta T_\gamma b_{\alpha\beta} b^{\alpha\gamma}\right)} 2 \delta(\varGamma^\beta_{\alpha\mu}) T^\mu g^{\alpha\gamma} g_{\beta\delta} T^{\delta}{}_{;\gamma} + T^\beta{}_{;\alpha} \delta(g^{\alpha\gamma}) g_{\beta\delta} T^{\delta}{}_{;\gamma} + T^\beta{}_{;\alpha} g^{\alpha\gamma} \delta(g_{\beta\delta}) T^{\delta}{}_{;\gamma}\right.\nonumber\\ &\quad\left. {}+ 2 \delta (b_{\alpha\beta}) g^{\alpha\delta}b_{\delta\gamma} T^\gamma T^\beta + T^\beta T^\gamma b_{\alpha\beta}b_{\delta\gamma} \delta(g^{\alpha\delta}) -2H v^{(n)} \delta t\left( T^\beta{}_{;\alpha} T_\beta{}^{;\alpha} + T^\beta T_\gamma b_{\alpha\beta} b^{\alpha\gamma}\right)\right]\mathrm{d}A. \end{align}$$

Focusing purely on the normal variation, we find

(2.23) \begin{align} \delta \mathcal{F}&= \int_{\mathcal{M}_t}\mathcal{K} \delta t\left\{ \left[ (v^{(n)} b_{\alpha}{}^\gamma)_{;\beta} - (v^{(n)}b_{\alpha\beta})^{;\gamma} - (v^{(n)}b^\gamma{}_\beta)_{;\alpha}\right]T^\alpha T^\beta{}_{;\gamma} + T^\beta{}_{;\alpha}T_{\beta;\gamma}b^{\alpha\gamma}v^{(n)} \right.\nonumber\\ &\quad - T^\beta{}_{;\alpha} T^{\gamma;\alpha}b_{\gamma\beta}v^{(n)} +(b^\alpha{}_\gamma T^\gamma T^\beta)_{;\beta\alpha}v^{(n)} - T^\gamma T^\beta \left(2H b_{\alpha\beta}b^\alpha{}_\gamma - K b_{\beta\gamma} \right)v^{(n)}\nonumber\\ &\left.\quad+\,T^\beta T^\gamma b_{\alpha\beta} b_{\delta\gamma}b^{\alpha\delta}v^{(n)}- H \left[ T^\beta{}_{;\alpha} T_\beta{}^{;\alpha} + T^\beta T_\gamma b_{\alpha\beta} b^{\alpha\gamma}\right]v^{(n)}\right\}\mathrm{d}A. \end{align}

Notice that the first terms from the variation of the covariant derivative include derivatives in the normal velocity. Integrating these by parts and pushing terms to the boundary, we can find the following functional variation in the bulk of the surface:

(2.24)\begin{align} \delta\mathcal{F}& = \int_{\mathcal{M}_t}\mathcal{K} v^{(n)}\delta t\left\{ b_{\alpha\beta}(T^\alpha T^\beta{}_{;\gamma})^{;\gamma} + b^\gamma{}_\beta(T^\alpha T^\beta{}_{;\gamma})_{;\alpha}- b_{\alpha}{}^\gamma (T^\alpha T^\beta{}_{;\gamma})_{;\beta} + T^\beta{}_{;\alpha}T_{\beta;\gamma}b^{\alpha\gamma}\right.\nonumber\\ &\quad - T^\beta{}_{;\alpha} T^{\gamma;\alpha}b_{\gamma\beta} + (b^\alpha{}_\gamma T^\gamma T^\beta)_{;\beta\alpha} - T^\gamma T^\beta \left(2H b_{\alpha\beta}b^\alpha{}_\gamma - K b_{\beta\gamma} \right) + T^\beta T^\gamma b_{\alpha\beta} b_{\delta\gamma}b^{\alpha\delta}\nonumber\\ &\left.\quad -\, H \left[ T^\beta{}_{;\alpha} T_\beta{}^{;\alpha} + T^\beta T_\gamma b_{\alpha\beta} b^{\alpha\gamma}\right]\right\}\,\mathrm{d}A + \text{boundary terms}. \end{align}

From this, and noting that the second and third terms cancel due to symmetry of $T^\alpha T^\beta$ and $b_{\alpha \beta }$, we find the forces in the normal direction from the free energy as

(2.25)\begin{align} &f^{(n)}_{{e}}={-}\mathcal{K}\left\{ b_{\alpha\beta}(T^\alpha T^\beta{}_{;\gamma})^{;\gamma} + T^\beta{}_{;\alpha}\left(T_{\beta;\gamma}b^{\alpha\gamma} - T^{\gamma;\alpha}b_{\gamma\beta}\right)+(b^\alpha{}_\gamma T^\gamma T^\beta)_{;\beta\alpha}\right.\nonumber\\ &\left.\quad {}- T^\gamma T^\beta \left(2H b_{\alpha\beta}b^\alpha{}_\gamma - K b_{\beta\gamma} \right) + T^\beta T^\gamma b_{\alpha\beta} b_{\delta\gamma}b^{\alpha\delta} - H \left[ T^\beta{}_{;\alpha} T_\beta{}^{;\alpha} + T^\beta T_\gamma b_{\alpha\beta} b^{\alpha\gamma}\right]\right\}. \end{align}

Note that the third term gives forces that go like the second derivative of the curvature tensor, but traced out along the directions of the nematic order parameter. Such a term is essentially an anisotropic bending rigidity that would not be found in the case where the covariant derivative, rather than surface derivative, was used in the free energy (Napoli & Vergori 2012; Santiago, Chacón-Acosta & Monroy 2019; Santiago & Monroy 2020). This gives equations that are significantly different to many of those currently analysed in the literature, both equilibrium and dynamical (Frank & Kardar 2008; Santiago 2018; Hoffmann et al. 2022; Salbreux et al. 2022).

Similarly for the tangential variations, we find the elastic force

(2.26)$$\begin{gather} f^{\alpha}_{{e}} ={-}\frac{\mathcal{K}}{2} \left\{ \left(T^\beta T^{\alpha;\gamma}\right)_{;\beta\gamma} + \left(T_{\beta;\gamma} T^{\beta;\alpha}\right)^{;\gamma} - \left(T_{\beta;\gamma} T^{\alpha;\gamma}\right)^{;\beta} - 2 \left(b^\alpha{}_\beta b^\gamma{}_\mu T^{\mu\beta}\right)_{;\gamma} \right.\nonumber\\ \left.{}- 2 \left( b^\gamma{}_\mu T^{\mu\beta}\right)_{;\beta} b^\alpha{}_\gamma + \left(T^\beta T^\gamma b_{\mu\beta} b^\alpha{}_{\gamma}\right)^{;\mu}\right\}. \end{gather}$$

This is essentially a generalised version of the Ericksen force (DeGennes & Prost 1993). For simplicity, we will neglect this tangential component in our later examples as it leaves the phenomenology of the equations unchanged. This approximation is taken in many exact calculations in active hydrodynamics (Hoffmann et al. 2022; Giomi et al. 2014; Kruse et al. 2004; Edwards & Yeomans 2009); however, in principle this term should be included in full nonlinear solutions.

2.4. Surface tension and director constraints

We consider two constraints upon our system whose contributions to the dynamical equations can be derived generically from a Rayleigh dissipation functional (DeGennes & Prost 1993; Doi 2011). However, we avoid a full variational treatment here for the sake of brevity, and instead simply state the contributions whose derivation can be found elsewhere (DeGennes & Prost 1993; Arroyo & DeSimone 2009; Marchetti et al. 2013).

The first constraint is that of constant area, or incompressibility, which is expressed by (2.8). The corresponding Lagrange multiplier is the surface tension $\zeta$, which acts isotropically via stresses $\sigma ^{(st)}_{\alpha \beta }=\zeta g_{\alpha \beta }$. Taking the surface divergence of $\sigma ^{(st)}$ gives the following contribution to the force balance condition:

(2.27)\begin{equation} \boldsymbol{f}^{c} = \boldsymbol{\nabla}^\alpha \zeta\boldsymbol{e}_\alpha + 2H \zeta \hat{\boldsymbol{n}}. \end{equation}

The second constraint is to fix the magnitude of the nematic director (DeGennes & Prost 1993). This is achieved by imposing

(2.28)\begin{equation} T_\alpha {D}_t T^\alpha = 0, \end{equation}

which implies $T^\alpha T_\alpha =\textrm {constant}$, with the constant specified by the initial conditions on $T^\alpha$ (Kruse et al. 2005). We label the associated Lagrange multiplier by $\lambda$, and the corresponding contribution to the director current (Prost, Jülicher & Joanny 2015) is just

(2.29)\begin{equation} J^\alpha_{c} ={-}\lambda T^\alpha. \end{equation}

This term can be viewed from a variational perspective as either a constraint on the Rayleigh dissipation functional of the form $\int \lambda T_\alpha {D}_t T^\alpha \,\mathrm {d}A$, or a contribution to the molecular field from a constraint on the free energy of the form $\int \frac {1}{2}\lambda \gamma T_\alpha T^\alpha \,\mathrm {d}A$ (DeGennes & Prost 1993).

2.5. Constitutive relation and dissipative forces

The viscous stress tensor in the tangent bundle is given as an Onsager expansion (Doi 2011; DeGennes & Prost 1993) in the thermodynamic fluxes. At lowest non-trivial order, it is given by

(2.30)\begin{equation} \sigma_{\alpha\beta} = 2 \eta d_{\alpha\beta} + \frac{\nu}{2}\left(T_\alpha h_\beta + T_\beta h_\alpha\right), \end{equation}

where $h_\alpha$ is the molecular field (2.20), $d_{\alpha \beta }$ is the rate-of-deformation tensor, $\eta$ is the shear viscosity, and $\nu$ gives the spin connection coefficients of the vector field (essentially the ratio of anisotropic viscosity to isotropic viscosity DeGennes & Prost 1993). Here, stable solutions require $|\nu |>1$, with $\nu <-1$ corresponding to rod-like nematics, and $\nu >1$ to disk-like nematics (Edwards & Yeomans 2009; Marchetti et al. 2013). Note that as we consider only incompressible fluids, we discard the bulk viscosity terms and associated spin connections (DeGennes & Prost 1993). The dissipative forces on our surface are then given as

(2.31)\begin{equation} \boldsymbol{f}^{d} = \boldsymbol{\nabla}_\beta \sigma^{\alpha\beta}\boldsymbol{e}_\alpha + \sigma^{\alpha\beta}b_{\alpha\beta} \hat{\boldsymbol{n}}. \end{equation}

For the terms in the tangent bundle we find

(2.32)\begin{equation} \boldsymbol{\nabla}_\beta\sigma^{\alpha\beta} = 2 \eta d^{\alpha\beta}{}_{;\beta} + \frac{\nu}{2}\left(T^\alpha h^\beta + T^\beta h^\alpha\right)_{;\beta}, \end{equation}

where we can unpack the first term to

(2.33)\begin{equation} 2\eta d^{\alpha\beta}{}_{;\beta} = \eta \left(v^{\alpha;\beta} + v^{\beta;\alpha} - 2 v^{(n)}b^{\alpha\beta}\right)_{;\beta} = \eta\varDelta v^\alpha + \eta v^\beta{}_{;\alpha\beta} - 2\eta \left(v^{(n)}b^{\alpha\beta}\right)_{;\beta}, \end{equation}

where $\varDelta =\boldsymbol {\nabla }_\alpha \boldsymbol {\nabla }^\alpha$ is the Bochner Laplacian. By making use of the Codazzi equation (A9) and the contracted Gauss equation (A12), we find

(2.34)\begin{equation} 2\eta d^{\alpha\beta}{}_{;\beta} = \eta\left[ \varDelta v^\alpha - 2\left(v^{(n)}H\right)^{;\alpha} + K v^{\alpha} + 2\left(2H g^{\alpha\beta} - b^{\alpha\beta}\right)v^{(n)}{}_{;\beta}\right]. \end{equation}

Thus the tangential forces are given by

(2.35)\begin{align} \sigma^{\alpha\beta}{}_{;\beta} &= \frac{\nu}{2}\left(T^\alpha h^\beta + T^\beta h^\alpha\right)_{;\beta}\nonumber\\ &\quad +\eta\left[ \varDelta v^\alpha - 2\left(v^{(n)}H\right)^{;\alpha} + K v^{\alpha} + 2\left(2H g^{\alpha\beta} - b^{\alpha\beta}\right)v^{(n)}{}_{;\beta}\right] . \end{align}

The normal forces are given by contracting the stress tensor with the second fundamental form

(2.36)\begin{equation} \sigma^{\alpha\beta}b_{\alpha\beta} = 2\eta b^{\alpha\beta}v_{\beta;\alpha} - 4\eta(2 H^2 - K)v^{(n)} + \nu T^{\alpha}h^{\beta}b_{\alpha\beta}. \end{equation}

2.6. Broken symmetry terms

We can also include broken symmetry terms in the stress tensor that contribute nothing to the overall dissipation as their dynamics are associated with Goldstone modes in the system, hence the name ‘broken symmetry’ (DeGennes & Prost 1993; Kruse et al. 2005). For vector fields, these contribute an antisymmetric part to the stress tensor of the form

(2.37)\begin{equation} \sigma^{(bs)}_{\alpha\beta} = \tfrac{1}{2}\left(T_\alpha h_\beta - T_\beta h_\alpha\right). \end{equation}

Note that these terms contribute to only the tangential forces as they vanish in the normal due to the symmetry of the second fundamental form upon index relabelling. The broken symmetry forces are thus given by

(2.38)\begin{equation} \boldsymbol{f}^{bs} = \boldsymbol{\nabla}_\beta \sigma^{(bs)\alpha\beta}\boldsymbol{e}_\alpha + \sigma^{(bs)\alpha\beta}b_{\alpha\beta} \hat{\boldsymbol{n}} = \tfrac{1}{2}\left(T^\alpha h^\beta - T^\beta h^\alpha\right)_{;\beta}\boldsymbol{e}_\alpha. \end{equation}

2.7. Director terms

Expanding out in an Onsager fashion for the director rate in terms of nematic relaxation, we find the couplings

(2.39)\begin{equation} J^{\alpha}_{T} = \gamma^{{-}1} h^\alpha -\nu d^\alpha{}_{\beta}T^\beta, \end{equation}

which give terms in a similar manner to the flat case (Kruse et al. 2005). Note that the constant $\nu$ is the same as for the director terms in the stress tensor by the Onsager reciprocal relations. Adding this together with the constraint current (2.29) gives the full Onsager expansion for the director rate as

(2.40)\begin{equation} {D}_t T^\alpha =\gamma^{{-}1} h^\alpha - \nu d^\alpha{}_\beta T^\beta - \lambda T^\alpha. \end{equation}

2.8. Active terms

We consider a simple extension to the tangential stress tensor that represents the dipolar-like active forces that are characteristic of many active nematic systems (Sanchez et al. 2012; Marchetti et al. 2013). For a detailed introduction to active matter, we refer the reader to the reviews Marchetti et al. (2013) and Ramaswamy (2017), and for active liquid crystals in particular to Doostmohammadi et al. (2018).

Active liquid crystals have generated significant interest in recent years due to several experimental realisations (Sanchez et al. 2012; Keber et al. 2014) that have revealed the fascinating interplay between active stresses and geometry of the director, particularly in the coupling of geometry of the surfaces to the dynamics of topological defects (Giomi et al. 2014; Khoromskaia & Alexander 2017; Pearce et al. 2019; Pearce 2020). In addition such systems have been suggested as minimal models for tissues (Blanch-Mercader et al. 2021a,b) and the actomyosin cell cortex (Kruse et al. 2005).

Here, we consider the standard form for the active nematic stress tensor:

(2.41)\begin{equation} \sigma^{{(a)}}_{\alpha\beta} = \varSigma Q_{\alpha\beta} = \varSigma \left(T_\alpha T_\beta - \tfrac{1}{2} g_{\alpha\beta}\right). \end{equation}

For $\varSigma >0$, such stresses are contractile in nature, and for $\varSigma <0$, they are extensile. This form represents the simplest form of anisotropic active stress; however, more complicated couplings are possible (Naganathan et al. 2014; Salbreux & Jülicher 2017; Salbreux et al. 2022). The active forces from (2.41) are given by

(2.42)\begin{equation} \boldsymbol{f}^a = \sigma^{{(a)}\alpha\beta}{}_{;\beta} \boldsymbol{e}_{\alpha}+ \sigma^{{(a)}\alpha\beta}b_{\alpha\beta}\hat{\boldsymbol{n}}. \end{equation}

2.9. Full dynamical equations

Putting together all our force balance terms, constraints and polarisation currents gives the following system of equations, which are essentially ordered fluid versions of the equations derived for isotropic fluid membranes in Arroyo & DeSimone (2009).

(2.43)\begin{align} &\text{Polarisation dynamics:}\nonumber\\ &\quad {D}_t T^\alpha =\gamma^{{-}1} h^\alpha - \nu d^\alpha{}_\beta T^\beta - \lambda T^\alpha.\end{align}

(2.44)\begin{align} &\text{Tangential force balance:}\nonumber\\ &\quad \frac{1}{2}\left(T^\alpha h^\beta - T^\beta h^\alpha\right)_{;\beta} +\eta\left[ \varDelta v^\alpha - 2\left(v^{(n)}H\right)^{;\alpha} + K v^{\alpha} + 2\left(2H g^{\alpha\beta} - b^{\alpha\beta}\right)v^{(n)}{}_{;\beta}\right]\nonumber\\ &\qquad + \frac{\nu}{2}\left(T^\alpha h^\beta + T^\beta h^\alpha\right)_{;\beta} + f^\alpha_{{e}} + \zeta^{;\alpha} + \sigma^{{(a)}\alpha\beta}{}_{;\beta}=0. \end{align}

(2.45)\begin{align} &\text{Normal force balance:}\nonumber\\ &\quad 2\eta b^{\alpha\beta}v_{\beta;\alpha} - 4\eta(2 H^2 - K )v^{(n)} + \nu T^{\alpha}h^{\beta}b_{\alpha\beta} + 2 H\zeta + f^{(n)}_{{e}} + \sigma^{{(a)}\alpha\beta}b_{\alpha\beta}=0. \end{align}

(2.46)\begin{align} &\text{Constraint equations (constant director and incompressibility):}\nonumber\\ &\quad T_\alpha{D}_t T^\alpha=0,\quad v^\alpha{}_{;\alpha}-2H v^{(n)}=0.\end{align}

(2.47)\begin{align} &\text{Closure between surface velocity and geometry:}\nonumber\\ &\quad \boldsymbol{V}= \frac{\mathrm{d}\boldsymbol{R}}{\mathrm{d}t}. \end{align}

2.10. Dimensionless numbers

There is an interesting point to make regarding the normal force balance equation. It contains the term $\eta b^{\alpha \beta }v_{\beta ;\alpha }$, which describes the curvature-induced coupling between viscous forces and shape. Such couplings have been discussed extensively for isotropic fluid membranes (Al-Izzi, Sens & Turner 2020a; Sahu et al. 2020a). These phenomena can be understood in terms of the dimensionless Scriven–Love number (Scriven 1960)

(2.48)\begin{equation} {SL} = \frac{O(\eta b^{\alpha\beta}v_{\beta;\alpha})}{O(\text{bending forces})} = \frac{\eta V L}{\mathcal{K}}, \end{equation}

where $V$ and $L$ are characteristic velocities and length scales, and we have assumed that $\textrm {bending forces}\sim \mathcal {K} L^{-3}$ (i.e., like the bending energy and Laplacian of the mean curvature).

In addition, however, there is a new anisotropic coupling due to terms $\sim \nu T^{\alpha }h^{\beta }b_{\alpha \beta }$ which, when compared to bending forces, could be thought of as a ‘liquid crystalline Scriven–Love number’:

(2.49)\begin{equation} {SL}^{(LC)} = \frac{O(\nu T_{\alpha}h_{\beta} b^{\alpha\beta})}{O(\text{bending forces})} = \nu. \end{equation}

As such, the dimensionless number associated with out-of-plane liquid crystalline dissipative forces is just the spin connection coefficient $\nu$.

In addition to this, there is also the dimensionless active stress. As this is a number comparing tangential stress to bending stress, we can consider it as an analogue of the Föppl–von Kármán number ${Y}$ that would typically compare stretching to bending forces in passive shell theory (Audoly & Pomeau 2010). In our case, this is given by

(2.50)\begin{equation} {Y}^{({Active})} = \frac{\varSigma L^2}{\mathcal{K}}. \end{equation}

Note that this implies that in highly curved geometries, bending forces will suppress active deformations.

3. Applications

To illustrate the potential interplay between geometry, ordering and flow, we provide some concrete examples. We focus first on the case where activity is not present, but where the highly curved geometry of a tube leads to couplings between the director and shape that are not present in the flat or close-to-flat cases studied in Salbreux et al. (2022). We then consider the ways in which active anisotropic stresses can drive tubes unstable, before finally considering the effects of activity on a topological defect located at the centre of a close-to-flat sheet.

3.1. Relaxation dynamics about a perturbed tube

We start with a simple example of a tube of radius $r(\theta,z,t)= r + \epsilon \,u(\theta,z,t)$, where $\epsilon$ is some dimensionless parameter that will be considered small. Such tubes have been shown in the case of isotropic membranes to have non-negligible Scriven–Love effects (Sahu et al. 2020a). The surface is prescribed by the vector $\boldsymbol {R}=(r\cos \theta,r\sin \theta,z)$. We can thus calculate the induced basis and metric

(3.1)\begin{equation} [g_{\alpha\beta}]=\left(\begin{matrix} r(r+2\epsilon u) & 0\\ 0 & 1 \end{matrix}\right)+O(\epsilon^2), \end{equation}

and the second fundamental form

(3.2)\begin{equation} [b_{\alpha\beta}]=\left(\begin{matrix} \epsilon u_{,\theta\theta}-\epsilon u-r & \epsilon u_{,\theta z }\\ \epsilon u_{,\theta z} & \epsilon u_{,zz} \end{matrix}\right)+O(\epsilon^2). \end{equation}

This gives mean and Gaussian curvature to first order as

(3.3)\begin{gather} H=\frac{\epsilon}{2}\left( u_{,zz}+\frac{1}{r^2}\,u_{,\theta\theta}+ \frac{1}{r^2}\,u\right)-\frac{1}{2 r}, \end{gather}

(3.4)\begin{gather} K={-}\frac{\epsilon u_{,zz}}{r}. \end{gather}

We write the director field as $\boldsymbol {T}=({\epsilon T^\theta }/{r})\boldsymbol {e}_\theta + (1+\epsilon T^z) \boldsymbol {e}_z +O(\epsilon ^2)$, where we have chosen the $O(1)$ term to be the unit vector in the $z$ direction such that the molecular field vanishes for the unperturbed state (Napoli & Vergori 2012). Thus at lowest order, the constraint equation on director unity becomes

(3.5)\begin{equation} \partial_t T^z=0, \end{equation}

and all the dynamics are in the $\theta$ direction, i.e. perpendicular to the initial zeroth order nematic ordering, as one would expect for the perturbative dynamics of a unit vector field. We write the velocity as $\boldsymbol{V} =\epsilon (v^\theta /r\boldsymbol {e}_\theta +v^z\boldsymbol {e}_z + \partial _t u \hat {\boldsymbol {n}})$, so the continuity equation becomes

(3.6)\begin{equation} \frac{\partial_t u}{r}+\frac{v^\theta_{,\theta}}{r}+v^z_{,z}=0. \end{equation}

The molecular field is given by

(3.7)\begin{equation} h^\alpha\boldsymbol{e}_\alpha = \mathcal{K} \epsilon \left(T^\theta_{,zz} + \frac{1}{r^2}\,T^\theta_{,\theta\theta} - \frac{1}{r^2}\,T^\theta + \frac{2}{r^2}\,u_{,\theta z}\right)\frac{1}{r}\,\boldsymbol{e}_\theta + \mathcal{K} \epsilon \left(\frac{T^z_{,\theta\theta}}{r^2} + T^z_{,zz}\right)\boldsymbol{e}_z, \end{equation}

and can be substituted to then find the polarisation rate equation whose components are given by

(3.8)\begin{align} &\boldsymbol{e}_\theta:\quad \epsilon \left[- \frac{\mathcal{K} }{\gamma r} \left(T^\theta_{,zz} + \frac{T^\theta_{,\theta\theta}}{r^2} - \frac{T^\theta}{r^2} + 2\,\frac{u_{,\theta z}}{r^2}\right)+\frac{1}{r} \left( \partial_t T^\theta + \frac{1}{2}\,v^\theta_{,z} +\frac{1}{2r}\, v^z_{,\theta}\right)\right.\nonumber\\ &\left.\qquad\quad{}+ \frac{1}{r} \left( \lambda T^\theta + \frac{\nu}{2}\,v^\theta_{,z} + \frac{\nu}{2r}\,v^z_{,\theta}\right)\right]=0, \end{align}

(3.9)\begin{align} &\boldsymbol{e}_z:\quad \lambda-\epsilon\left[\frac{\mathcal{K} }{\gamma} \left(\frac{1}{r^2}\,T^z_{,\theta\theta}+ T^z_{,zz}\right) + \partial_t T^z + \lambda T^z + \nu v^z_{,z}\right]=0. \end{align}

The modified covariant Stokes equation (tangential force balance) is given componentwise by

(3.10)\begin{align} &\boldsymbol{e}_\theta:\quad \frac{\zeta_{,\theta} (r-2 \epsilon u)}{r^3}+\frac{\mathcal{K} (\nu -1) \epsilon}{2 r^3} \left(r^2 T^\theta_{,zzz} - T^\theta_{,z} + T^\theta_{,\theta\theta z} + 2 u_{,\theta zz}\right)\nonumber\\ &\qquad\quad+\frac{\eta \epsilon}{r^3} \left(r^2 v^\theta_{,zz} + \partial_t u_{,\theta} + v^\theta_{,\theta\theta}\right)=0, \end{align}

(3.11)\begin{align} &\boldsymbol{e}_z:\quad\frac{\eta \epsilon}{r^2} \left(r^2 v^z_{,zz}-r \partial_t u_{,z} + v^z_{,\theta \theta}\right)+\zeta_{,z} = 0. \end{align}

The normal components of force due to the liquid crystal free energy are more complicated to calculate, however. Nevertheless, at $O(\epsilon )$, only the third term of (2.25) contributes, giving

(3.12)\begin{equation} \left(b^\alpha{}_\gamma T^\gamma T^\beta\right)_{;\beta\alpha} = \epsilon\left[u_{,zzzz}-\frac{1}{r^2}\,T^\theta_{,z\theta} +\frac{1}{r^2}\,u_{,zz\theta\theta}\right]+O(\epsilon^2), \end{equation}

which gives the shape equation

(3.13)$$\begin{gather} \frac{\mathcal{K} \epsilon}{r^2} \left(r^2 u_{,zzzz} - T^\theta_{z\theta} + u_{,zz\theta\theta}\right) -\frac{\zeta}{r^2} \left[ \epsilon\left(r^2 u_{,zz} + u_{,\theta\theta} + u\right)-r\right]\nonumber\\ {}+\frac{2 \eta \epsilon}{r^2} \left(\partial_t u + v^\theta_{,\theta}\right)=0. \end{gather}$$

Taking the case where $\epsilon =0$, we find a ground state with

(3.14)$$\begin{gather} \lambda=0, \end{gather}$$

(3.15)$$\begin{gather}\zeta = 0, \end{gather}$$

(3.16)$$\begin{gather}\boldsymbol{T}= \boldsymbol{e}_{z}, \end{gather}$$

as required. Note that as the bending energy term is anisotropic, it gives no characteristic length scale of the tube as compared to the case of a lipid bilayer, for example, where the ground-state radius of the tube is set by the ratio of isotropic bending energy to surface tension ($r_0=\sqrt {\kappa /2\zeta }$) (Zhong-Can & Helfrich 1989; Nelson, Powers & Seifert 1995; Gurin, Lebedev & Muratov 1996; Fournier & Galatola 2007; Powers 2010; Boedec, Jaeger & Leonetti 2014).

We now take $\zeta =\epsilon \zeta$, $\lambda =\epsilon \lambda$, and take the Fourier transform in space $\bar {f}_{q,m}=(1/4{\rm \pi} ^2)\int \,\mathrm {d}z\,\mathrm {d}\theta \,f(z,\theta )\exp ({-\textrm {i} m \theta -\textrm {i} q z})$. Using each of (3.5), (3.6), (3.10), (3.9) and (3.13) leaves simply two dynamical equations for $\bar {u}_{qm}$ and $\bar {T}^\theta _{qm}$, which are given in dimensionless form as

(3.17) \begin{equation} \partial_{\tilde{t}} \left(\begin{matrix} \bar{T}^\theta_{qm}\\ \bar{u}_{qm} \end{matrix}\right)=\boldsymbol{\mathsf{A}} \cdot\left(\begin{matrix} \bar{T}^\theta_{qm}\\ \bar{u}_{qm} \end{matrix}\right) = \left(\begin{matrix} {\mathsf{A}}_{11} & {\mathsf{A}}_{12}\\ {\mathsf{A}}_{21} & {\mathsf{A}}_{22}\end{matrix}\right)\cdot\left(\begin{matrix} \bar{T}^\theta_{qm}\\ \bar{u}_{qm} \end{matrix}\right), \end{equation}

where componentwise,

(3.18) \begin{align} \left. \begin{aligned} {\mathsf{A}}_{11} = \frac{m^2 \left(-\left(Q^2 \left(4 \bar\eta +\nu ^2+1\right)+1\right)\right)-Q^2 \left(Q^2+1\right) \left(4\bar\eta +(\nu -1)^2\right)}{4 Q^2},\cr {\mathsf{A}}_{12} = \frac{m \left(m^4-2 m^2 \left((\nu -1) Q^2+1\right)+(1-2 \nu ) Q^4-2 Q^2 \left(4 \bar{\eta} +(\nu -1)^2\right)\right)}{4 Q},\cr {\mathsf{A}}_{21} = \frac{m \left({-}2 \nu Q^2 \left(m^2+Q^2+1\right)+m^2+Q^2\right)}{4 Q^3},\cr {\mathsf{A}}_{22}={-}\frac{m^6+m^4 \left(3 Q^2-2\right)+m^2 Q^2 \left(4 \nu +3 Q^2-2\right)+Q^6}{4 Q^2}, \end{aligned} \right\} \end{align}

where time has been normalised by $t=\tau \tilde {t}$ with $\tau =\eta r^2/\mathcal {K}$, $\bar {\eta }=\eta /\gamma$, $Q=rq$, and $\bar {u}$ has been non-dimensionalised by $r$. Note that the off-diagonal elements couple linearly in $mQ$. That is, the sign of $\bar {T}^{\theta }_{qm}$ selects a handedness of coupling to the shape deformations.

In contrast to the case of a flat membrane, this shows that in highly curved environments, the relaxation of shape and orientational ordering cannot be decoupled even in the case when the ground state has no intrinsic curvature. This is true for all the modes on the tube, with the exception of the $m=0$ case where the ordering and shape decouple. In figure 2, we plot the negatives of the eigenvalues $\{\varLambda _1,\varLambda _2\}$ of the matrix $\boldsymbol{\mathsf{A}}$ as functions of wavenumber $Q$ for the first $m=0,1,2,3$ modes. These can be interpreted as the passive relaxation modes that return perturbations back to the ground state.

Figure 2. Relaxation rates for a perturbed liquid-crystal tube. Here, $\varLambda _i$ are the two eigenvalues of the growth matrix given in (3.17), that is, the growth rate of the spatial Fourier modes with time non-dimensionalised by $\tau =\eta r^2/\mathcal {K}$, where $\eta$ is the 2-D viscosity, $r$ is the tube radius, and $\mathcal {K}$ is the liquid crystalline elastic modulus. These are plotted against dimensionless wavenumber $Q=q r$ ($z$ direction Fourier variable) for the first four integer modes in $m$ (the $\theta$ Fourier variable). The dimensionless viscosity is $\bar \eta =1$, and the spin connection is $\nu =-1.5$.

3.2. Active nematic liquid crystals

In this subsection, we will consider the effects of a non-zero active stress on the stability of nematic tubes, and on the morphology of a surface with a $+1$ defect located at the origin. In particular, we will examine the effects of changing the sign of the active stress (i.e. contractile versus extensile) on the morphology and surface instabilities.

3.2.1. Active ruffling and pearling instabilities in tubes

Using our equation for the active stress, we can find that the normal part of the active force for a tube is given by

(3.19)\begin{equation} \boldsymbol{f}^a\boldsymbol{\cdot}\hat{\boldsymbol{n}} = \sigma^{{(a)}\alpha\beta}b_{\alpha\beta}= \frac{\varSigma \left[\epsilon\left(r^2 u_{,zz}-u_{,\theta\theta} - u\right)+r\right]}{2 r^2}, \end{equation}

and the tangential parts by

(3.20)\begin{equation} (\mathbb{I}-\hat{\boldsymbol{n}}\otimes\hat{\boldsymbol{n}})\boldsymbol{\cdot}\boldsymbol{f}^a=\sigma^{{(a)}\alpha\beta}{}_{;\beta}\,\boldsymbol{e}_\alpha = \frac{\varSigma \epsilon T^\theta_{,z}}{r}\,\boldsymbol{e}_\theta + \frac{\varSigma \epsilon \left(2 r T^z_{,z} + T^\theta_{,\theta} +u_{,z}\right)}{r}\,\boldsymbol{e}_z. \end{equation}

where $\mathbb{I}$ is the identity matrix in $\mathbb{R}^3$.

Following a similar procedure as before, we now find a different ground-state surface tension at $\epsilon =0$ for the unperturbed tube of $\zeta = \varSigma /2 +O(\epsilon )$. Now following the same procedure as before, of Fourier transforming the equations around this ground state, we can find the dynamical equations for shape and alignment. Here, we will consider only the axisymmetric deformations ($m=0$) for simplicity. This leads to the following equations for $\bar {u}_{q}$ and $\bar {T}^\theta _{q}$:

(3.21)$$\begin{gather} \partial_{\tilde{t}}\bar{T}^{\theta}_{q}={-}\frac{(Q^2+1) \left((\nu -1)^2+4 \bar\eta \right)-2 (\nu -1) \bar\varSigma }{4}\,\bar{T}^\theta_q, \end{gather}$$

(3.22)$$\begin{gather}\partial_{\tilde{t}}\bar{u}_{q} ={-}\frac{Q^4+(Q^2-1) \bar{\varSigma} }{4}\,\bar{u}_q, \end{gather}$$

where $t=\tau \tilde {t}$, with $\tau =\eta r^2/\mathcal {K}$, $\bar {\eta }=\eta /\gamma$, $\bar {\varSigma }=\varSigma r^2/\mathcal {K}$, $Q=rq$, and $\bar {u}$ has been non-dimensionalised by $r$. Note that $\bar \varSigma$ is essentially a ratio of surface forces to bending energy and can thus be viewed as an ‘active Föppl–von Kármán number’ that we discussed earlier.

First, we will consider the second equation describing the shape dynamics. The growth rate for the shape perturbation, $\bar {u}_q$, is given by

(3.23)\begin{equation} \varLambda_u(Q,\bar{\varSigma})={-}\frac{Q^4+\left(Q^2-1\right) \bar{\varSigma}}{4}. \end{equation}

This can be driven unstable for

(3.24)\begin{equation} \bar\varSigma\leq \frac{-Q^4}{Q^2-1}. \end{equation}

For the case of an extensile active stress ($\varSigma <0$), this leads to an instability of a finite range of $Q>1$ peaked around a specific wavelength; see figure 3. The fastest growing mode of this instability is found at $Q^\star =\sqrt {-\bar \varSigma /2}$, and as this occurs at $Q>1$, leads to ruffling-like undulations in the membrane. This makes sense heuristically as the extensile stresses are pointing along the tube thus generating forces that act to increase the surface area of the tube, hence the ruffling.

Figure 3. Extensile instability causes a ruffling-like deformation in the shape of the tube. Here, $\varLambda _u(Q,\bar {\varSigma })$ is the growth rate of the spatial Fourier modes, with time non-dimensionalised by $\tau =\eta r^2/\mathcal {K}$, where $\eta$ is the 2-D viscosity, $r$ is the tube radius, and $\mathcal {K}$ is the liquid crystalline elastic modulus. The active stress is non-dimensionalised as $\bar \varSigma =\varSigma r^2/\mathcal {K}$. Inset shows a representative example of such an instability.

In the case of contractile stresses ($\varSigma >0$), we find an instability with fastest growing mode in the $Q\to 0$ limit; see figure 4(a). This instability is analogous to a classical Rayleigh–Plateau instability (Rayleigh 1892; Tomotika 1935) and similar to the pearling instabilities seen in fluid membrane tubes (Gurin et al. 1996; Boedec et al. 2014; Narsimhan, Spann & Shaqfeh 2015). In reality, such an instability does not occur at infinite length scales as the dissipative time scale in the ambient media damps the longer-wavelength modes. We can approximate the bulk dissipation by modifying our shape dynamics equation as (Nelson et al. 1995; Gurin et al. 1996; Powers 2010; Al-Izzi et al. 2020b; Boedec et al. 2014)

(3.25)\begin{equation} \varLambda_u(Q,\bar{\varSigma})={-}\frac{Q^4+\left(Q^2-1\right) \bar{\varSigma}}{4+8 Q^{{-}2}\tilde{L}_{{SD}}^{{-}1}}, \end{equation}

where $\tilde {L}_{{SD}} = \eta /(\eta _b r)$ is the dimensionless Saffman–Delbrück length, and $\eta _b$ is the ambient viscosity (Saffman 1975; Saffman & Delbrück 1975). Here, this leads to a long-wavelength instability as the contractile stress tries to minimise the surface to volume ratio of the tube. This gives a finite wavelength to the fastest growing mode set by the Saffman–Delbrück length; see figure 4(b). This instability is similar to the isotropic contractile instabilities found previously in fluid membranes (Mietke, Julicher & Sbalzarini 2019).

Figure 4. Contractile instability causes a pearling-like deformation in the shape of the tube. Here, $\varLambda _u(Q,\bar {\varSigma })$ is the growth rate of the spatial Fourier modes, with time non-dimensionalised by $\tau =\eta r^2/\mathcal {K}$, where $\eta$ is the 2-D viscosity, $r$ is the tube radius, and $\mathcal {K}$ is the liquid crystalline elastic modulus. The active stress is non-dimensionalised as $\bar \varSigma =\varSigma r^2/\mathcal {K}$. (a) Instability in the absence of an ambient fluid. (b) Instability when an approximation to ambient hydrodynamics in the long-wavelength limit is used. Here, $\tilde {L}_{{SD}}= {\eta }/{\eta _b r}$ is the dimensionless Saffman–Delbrück length given by the ratio of 2-D to three-dimensional viscosity ($\eta _b$) non-dimensionalised by tube radius. Inset shows an example growth of a surface undulation for the case with bulk fluid.

We now turn our attention to the growth rate of the director deviations, which is given by

(3.26)\begin{equation} \varLambda_T(Q,\bar{\varSigma},\bar{\eta},\nu)={-}\frac{\left(Q^2+1\right) \left(4 \bar\eta +(\nu -1)^2\right)-2 (\nu -1) \bar\varSigma}{4}. \end{equation}

This can also have a change in sign when in the extensile or contractile regime, depending on the sign of $\nu$ ($\nu <-1$ corresponds to rod-like nematics, and $\nu >1$ to disk-like). The stability condition is given by

(3.27)\begin{equation} \bar\varSigma\geq \frac{(Q^2+1)\left(4\bar\eta+(\nu-1)^2\right)}{2(\nu-1)}, \end{equation}

which leads to a spontaneous bend instability in the longest wavelengths of the tube; see figure 5. This instability is well known in flat geometry in the case of extensile stress and rod-like nematics ($\nu <-1$), where it is known to lead to active turbulence (Marchetti et al. 2013).

Figure 5. (a) Extensile bend instability in texture on the surface of the tube with rod-like nematics. (b) Contractile bend instability in texture on the surface of the tube with disk-like nematics. Here, $\varLambda _T(Q,\bar {\varSigma })$ is the growth rate of the spacial Fourier modes, with time non-dimensionalised by $\tau =\eta r^2/\mathcal {K}$, where $\eta$ is the 2-D viscosity, $r$ is the tube radius, and $\mathcal {K}$ is the liquid crystalline elastic modulus. The active stress is non-dimensionalised as $\bar \varSigma =\varSigma r^2/\mathcal {K}$. The dimensionless viscosity is $\bar \eta =1$, and the spin connection is (a) $\nu =-1.5$, and (b) $\nu =1.5$. Insets show an example of the bend instability at the longest wavelength of the tube.

In the limit $Q\to 0$, this criterion becomes $\bar \varSigma \geq (4\bar \eta +(\nu -1)^2)/2(\nu -1)$, in comparison to the flat case where the instability is thresholdless (Marchetti et al. 2013). This is due directly to the correct use of the surface derivative as the texture needs sufficient active stress to overcome the elastic stress the bend induces by forcing the texture to bend around the tube. Because of this threshold, it is interesting to note that the shape instability precedes the bend instability, suggesting that it should be possible to generate shape changes before one sees active turbulence. The interplay between this instability and the shape equations beyond linear order is likely a very rich topic as this director instability would likely couple to helical deformation modes leading to a spontaneous chiral symmetry breaking. However, such a topic is beyond the scope of the analysis in this paper.

3.2.2. Active topological defect deformations

Here, we consider a planar membrane in polar Monge coordinates, where the surface is parametrised by the Cartesian vector $\boldsymbol {R}=(r\cos \theta,r\sin \theta,\epsilon z)$. For simplicity, we will consider only axisymmetric steady states, thus $z(r,\theta )=z(r)$. The metric and second fundamental form are given as

(3.28)\begin{gather} {}[g_{\alpha\beta}] = \left( \begin{array}{@{}cc@{}} 1 & 0 \\ 0 & r^2 \end{array} \right) +O(\epsilon^2), \end{gather}

(3.29)\begin{gather} {}[b_{\alpha\beta}] = \left( \begin{array}{@{}cc@{}} \epsilon z_{,rr} & 0 \\ 0 & r \epsilon z_{,\theta} \end{array} \right) + O(\epsilon^2), \end{gather}

up to first order in $\epsilon$. Thus we find $H= ({\epsilon }/{2})(({1}/{r})z_{,r}+z_{,rr})+O(\epsilon ^2)$ and $K=0+O(\epsilon ^2)$. We take the polarisation texture to be $\boldsymbol {T}=\cos \phi \,\boldsymbol {e}_{r} + ({1}/{r})\sin \phi \,\boldsymbol {e}_\theta$, where $\phi$ is a constant such that there is a $+1$ topological defect located at $r=0$. The continuity equation then yields $v^r=0$, so we are left to solve for $z(r,t)$, $\zeta (r,t)$, $\lambda (r,t)$ and $v^\theta (r,t)$.

At lowest order in $\epsilon$, the equations are independent of $\dot {z}$, so we look for steady states in the nematic order parameter. Our choice of $\boldsymbol {T}$ trivially satisfies the unit magnitude constraint. We now make use of the fact that at lowest order, the tangential force balance and polarisation equations are just given by their flat counterparts (that is, they have no $O(\epsilon )$ term), and the shape equation is given entirely by $O(\epsilon )$ terms (Kruse et al. 2005; Hoffmann et al. 2022).

The polarisation equations become

(3.30)$$\begin{gather} (\nu \cos (2 \phi )-1) \left( v^\theta_{,r}-\frac{v^\theta}{r}\right)=0, \end{gather}$$

(3.31)$$\begin{gather}\nu \sin (\phi ) \cos (\phi ) \left( v^\theta_{,r}-\frac{v^\theta}{r}\right)+\lambda +\frac{\mathcal{K} }{\gamma r^2}=0, \end{gather}$$

which, assuming $\nu >1$ (disk-like nematics), gives

(3.32)$$\begin{gather} \phi ={\pm} \frac{1}{2}\arccos\left[\frac{1}{\nu}\right], \end{gather}$$

(3.33)$$\begin{gather}\lambda ={-} \frac{\mathcal{K}}{r^2 \gamma} - \nu\sin (\phi)\cos(\phi)\left[v^\theta_{,r}-\frac{v^\theta}{r}\right]. \end{gather}$$

Substituting the solution for $\phi$ into the tangential force balance gives

(3.34)$$\begin{gather} \zeta_{,r} + \frac{\mathcal{K} \nu }{r^3}+\frac{\varSigma }{\nu r} = 0, \end{gather}$$

(3.35)$$\begin{gather}r \left(\eta v^\theta_{,r} + \eta r v^\theta_{,rr} \pm \sqrt{1-\frac{1}{\nu ^2}}\,\varSigma \right)-\eta v^\theta = 0, \end{gather}$$

for which solutions are

(3.36)$$\begin{gather} \zeta = \frac{\mathcal{K}\nu}{2 r^2} - \frac{\varSigma}{\nu} \log\left[\frac{r}{r_{{max}}}\right]+\zeta_0, \end{gather}$$

(3.37)$$\begin{gather}v^\theta ={\mp} \frac{\varSigma}{2\eta} \sqrt{1-\frac{1}{\nu^2}}\,r \log\left[\frac{r}{r_{{max}}}\right], \end{gather}$$

where $\zeta _0 + \mathcal {K}\nu /2 r^2_{{max}}$ is the surface tension at $r=r_{{max}}$ (figure 6). This solution is identical to that found in Kruse et al. (2004), and is one of the classical results of polar active gel theory in a flat geometry. Notice that the surface tension diverges as $r\to 0$ due to the presence of the defect. This divergence in shape can be avoided by introducing a short wavelength cut-off $r_c$, or by considering a more general Landau–de Gennes free energy that allows for a nematic isotropic phase transition (DeGennes & Prost 1993).

Figure 6. (a) Defect surface tension $\zeta (r)$ as a function of radius $r$ about a $+1$ defect centred on $r=0$. Inset is defect texture. (b) Velocity field around the defect. Here, we have introduced a small cut-off radius at $r=0.03$, where lengths are non-dimensionalised by the radius of the boundary $r_{{max}}=1$. Surface tension is given by $\bar \zeta _0=\zeta _0 r_{{max}}^2/\mathcal {K}=1.0$, spin connection is $\nu =1.5$, $r_c=0.03$ and $c=-0.05$, where $c$ essentially defines the contact angle at the boundary. The active stress is non-dimensionalised by $\bar \varSigma = \sigma r_{{max}}/\mathcal {K}$. We plot for both positive (contractile) and negative (extensile) values of active stress to show promotion/suppression of the deformation in each case.

Substituting our solution for the surface tension into the normal force balance equation yields the dimensionless shape equation

(3.38)$$\begin{gather} \frac{z_{,r}}{r^3} \left(7-\nu \left(2 \bar\zeta_0 r^2+5\right)+2 r^2 \bar\varSigma \log (r)+r \left(\sqrt{\nu ^2-1}+r \bar\varSigma \right)\right)\nonumber\\ {}-\frac{z_{,rr}}{r^2} \left(r^2 (2 \bar\zeta_0 \nu + \bar\varSigma )-2 r^2 \bar\varSigma \log (r)+4\right)\nonumber\\ +\,(\nu +1) \left( z_{,rrrr} + \frac{2}{r}\,z_{,rrr}\right)=0, \end{gather}$$

where lengths have been non-dimensionalised by $r_{{max}}$, and energies by $\mathcal {K}$. We can solve this equation numerically from the boundary ($r=1$ in our dimensionless units) up to a small cut-off $r_c$. We solve with zero mean curvature and derivative in curvature at $r=r_{{max}}=1$ – at lowest order, this is $z'(r_{{max}})=-z''(r_{{max}})=z'''(r_{{max}})=c=\textrm {Const.}$ – and fix $z(r_{{max}})=0$ at the boundary. The constant $c$ essentially prescribes the contact angle at the boundary. To solve this numerically, we make use of Mathematica (WolframResearch, Champaign, IL).

Solutions to this for varying values of active stress are plotted in figure 7 with $\bar \zeta _0=1.0$, $\nu =1.5$, $r_c=0.03$ and $c=-0.05$. For $\bar \varSigma =0$, we find a convex cusp solution where the stress from the defect causes the surface to buckle. Note that this is qualitatively similar to the full nonlinear pseudo-sphere cusp found in (Frank & Kardar 2008), although the quantitative details of our shape differ significantly due to our inclusion of the extrinsic curvature term in the Frank free energy, and thus the anisotropic bending energies in our shape equation (fourth- and third-order terms) making a full analytical nonlinear solution of our equations impossible. For the extensile case, the protrusion decreases in height. The reason for this is due directly to our inclusion of the extrinsic terms in the Frank free energy and the convex shape of the passive solution. Extensile stresses lead to active forces that act to increase bend, in this case bend due to the deformation along the surface, thus pushing the surface down and suppressing the deformation. The opposite is true in the contractile case, where the active forces act to flatten bend, thus pushing the surface upwards. A simple example of these types of effect was discussed in the context of an active fingering instability in Alert (2022). In addition, we show that as the spin connection $\nu$ (or liquid crystalline Scriven–Love number) is increased, the spiral defect texture goes from aster-like to vortex-like as $\nu$ goes to $\infty$. As this happens, the bend along the surface goes to zero, and the height of the defect, $z(r_{c})$, converges in the extensile, contractile and passive cases, as expected.

Figure 7. (a) Surface heights $z(r)$ as a function of radius $r$ about a $+1$ defect centred on $r=0$. Here, we have introduced a small cut-off radius at $r=0.03$, where lengths are non-dimensionalised by the radius of the boundary $r_{{max}}=1$. Surface tension is given by $\bar \zeta _0=\zeta _0 r_{{max}}^2/\mathcal {K}=1.0$, spin connection is $\nu =1.5$, $r_c=0.03$ and $c=-0.05$, where $c$ essentially defines the contact angle at the boundary. The active stress is non-dimensionalised by $\bar \varSigma = \sigma r_{{max}}/\mathcal {K}$. We plot for both positive (contractile) and negative (extensile) values of active stress to show promotion/suppression of the deformation in each case. Inset is an example surface with the texture shown on top. (b) Maximum defect height $z(r_c=0.03)$ plotted against spin connection $\nu$ (or liquid crystalline Scriven–Love number) in the passive, contractile and extensile cases.

Note that our results here are different from those seen in Hoffmann et al. (2022), where the effects of contractile and extensile forces are switched. This is straightforward to understand since Hoffmann et al. (2022) did not consider the extrinsic coupling of the director, and in addition included an isotropic bending energy. This causes the passive shape to be regularised around the defect and to be concave near the defect where the active forces are strongest, leading to a switch in sign of the normal force due to activity when compared to our convex passive shape. Such subtle interplay between passive and active stresses suggests a rich phenomenology of possible nonlinear solutions to such systems, and that it may be possible for both extensile and contractile systems to achieve a similar morphology by the varying of passive parameters.

It is interesting to note that the contractile protrusions we find are similar to those seen during Hydra morphogenesis in the underlying contractile actomyosin network (Maroudas-Sacks et al. 2021; Vafa & Mahadevan 2022). There, the $+1$ defects form the basis of protrusions that develop into ‘limbs’.

4. Discussion

In this paper, we have developed a fully covariant hydrodynamic theory of active nematic fluids on deformable surfaces, deriving equations for normal and tangential force balance along with an equation for order parameter dynamics. Focusing on the case of the one-constant Frank free energy, we identify three dimensionless numbers: two Scriven–Love numbers associated with the ratio of normal viscous forces to bending forces, and an active analogue of the Föppl–von Kármán number, comparing tangential active stress to bending forces.

We then consider the relaxation dynamics, in shape and order parameter, of a nematic tube with no active forcing, showing that there is a non-trivial coupling between shape and director relaxation in the case of the non-axisymmetric modes. Motivated by the recent interest in active nematic fluids as models of morphogenetic processes, we further consider the effect of an active $\boldsymbol{\mathsf{Q}}$-tensor term on tube morphology. Here, we show that there are several new instabilities in both the contractile and extensile cases, which we compare to similar cases in flat geometry liquid crystals and isotropic fluid membranes. Finally, we consider the effect of activity on the surface morphology around a $+1$ topological defect, where anisotropic stresses drive or suppress protrusion of the defect, dependent on whether stresses are contractile or extensile, respectively.

An interesting extension of the problems considered here would be the effect of $1/2$-integer defects on the shape. In addition to breaking axisymmetry, this presents an additional complication in that $+1/2$-integer defects are known to self-propel in active liquid crystals (Giomi et al. 2014). We speculate that such effects would persist (at least in the small deformation limit) and would lead to self-propelled travelling waves in the shape. We aim to explore this phenomenology in detail in future work.

More generally, we believe that the framework developed here has applications in a wide range of systems, bridging length and time scales. Our chief interest throughout was to develop the equations in a clear, systematic way that laid bare the basic phenomenology without recourse to biological specifics. With the addition of relevant concentration fields describing morphogens, growth factors and other signalling molecules, these equations could form the basis for a nematic theory of deformable epithelial tissues (Jülicher et al. 2018; Al-Izzi & Morris 2021). There are also additional areas of potential application in the field of lipid bilayer dynamics; when augmented with isotropic bending energy terms, these equations could form the basis for a dynamic theory of tilt-chiral lipid bilayers, extending earlier work considering only energetics (Selinger et al. 1996). It is also plausible that this is the natural framework to model a fluid bilayer coupled to a thin layer of active filaments, e.g. actin (Simon et al. 2019), microtubules (Keber et al. 2014) or engineered filaments such as DNA filaments (Jahnke et al. 2022).

A major open challenge in the field of covariant hydrodynamics is developing general stable numerical methods to provide solutions beyond the linear perturbation regime or simple axisymmetric cases (Mietke et al. 2019). A large body of work exists for such problems in the case of passive and active isotropic fluids based on unfitted finite elements, arbitrary Lagrangian–Eulerian finite elements or isogeometric analysis (Barrett, Garcke & Nürnberg 2016; Torres-Sánchez, Millán & Arroyo 2019; Vasan et al. 2020; Sahu et al. 2020b), but to our knowledge, this has yet to be extended to nematic fluids on moving curved surfaces. It is important to note that the equations derived here would likely need to be modified to describe the $\boldsymbol{\mathsf{Q}}$-tensor dynamics rather than the nematic order parameter $\boldsymbol {T}$ so as to deal correctly with $1/2$-integer defects numerically. Solving such tensor PDEs on curved surfaces is challenging, with issues relating to the discontinuity of basis functions across elements, although some progress has been made recently in approximating tensor fields numerically using local Monge approximations (Torres-Sánchez, Santos-Oliván & Arroyo 2020).

Current methods for solving nemato-hydrodynamics are often hybrid lattice Boltzmann codes (Denniston, Orlandini & Yeomans 2001; Binysh et al. 2020), and such methods have been used along with phase fields to approximate interface dynamics (Metselaar et al. 2019; Hoffmann et al. 2022). We believe that it would also be useful to develop tools to solve the full covariant equations of a deformable mesh using finite element methods so as to provide numerical methods that more clearly map to a geometric analytical framework, and thus provide a clearer conceptual link between hydrodynamics and geometry. We therefore welcome further work in this area.