Article contents
Morphologies and dynamics of micro-droplet impact onto an idealised scratch
Published online by Cambridge University Press: 26 August 2021
Abstract
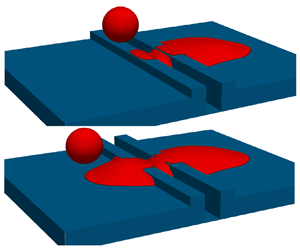
As inkjet technology develops to produce smaller droplets, substrate features such as accidental scratches or manufacturing defects can potentially affect the outcome of printing, particularly for printed electronics where continuous tracks are required. Here, the deposition of micro-droplets onto a scratch of commensurate size is studied. The scratch is considered as a groove of rectangular cross-section, with rectangular side ridges representing material displaced from the substrate, and seven equilibrium morphologies are identified as a result of inertial spreading, contact-line pinning, imbibition into the scratch and capillary flow. A regime map is constructed in terms of scratch depth and width, and theoretical estimates of the regime boundaries are developed by adapting droplet spreading laws for flat surfaces to account for liquid entering the scratches. Good agreement is seen with numerical results obtained using a graphical processing unit-accelerated three-dimensional multiphase lattice Boltzmann model validated against published experiments, and the influences of Reynolds number, Weber number and advancing and receding contact angles are explored. Negative and positive implications of the results for printing applications are discussed and illustrated via multiple-droplet simulations of printing across and along scratches.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
Al-Ghaithi et al. supplementary movie 6
Capillary morphology example. Capillary flow occurs after droplet deposition. The frame rate changes in the video because of the difference in frame rate between impact spreading and capillary flow.
Al-Ghaithi et al. supplementary movie 7
Simulations of printing of consecutive droplets across scratches of two depths. The width and depths are chosen within the split semi-imbibed morphology range. Splitting occurs for the first depth as expected but consecutive droplets push back and cause re-coalescence. Splitting occurs and persists for the second depth.
- 9
- Cited by


