Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-25T23:09:49.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of a viscous slug on heterogeneous surfaces: crossover from stick–slip to steady sliding

Published online by Cambridge University Press:  10 October 2023

Bauyrzhan K. Primkulov Open the ORCID record for Bauyrzhan K. Primkulov [Opens in a new window] ,
Amir A. Pahlavan Open the ORCID record for Amir A. Pahlavan [Opens in a new window] ,
Luis Cueto-Felgueroso Open the ORCID record for Luis Cueto-Felgueroso [Opens in a new window]  and
Ruben Juanes Open the ORCID record for Ruben Juanes [Opens in a new window]
Bauyrzhan K. Primkulov
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Amir A. Pahlavan
Affiliation:
Department of Mechanical Engineering and Materials Science, Yale University, New Haven, CT 06520, USA
Luis Cueto-Felgueroso
Affiliation:
Department of Civil Engineering: Hydraulics, Energy and Environment, Universidad Politécnica de Madrid, 28040 Madrid, Spain
Ruben Juanes*
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: juanes@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

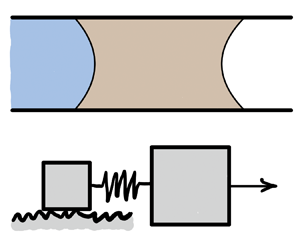
We present a theoretical study of viscous slug motion inside a microscopically rough capillary tube, where pronounced stick–slip motion can emerge at slow displacement rates. The mathematical description of this intermittent motion can be reduced to a system of ordinary differential equations, which also describe the motion of a pendulum inside a fluid-filled rotating drum. We use this analogy to show that the stick–slip motion transitions to steady sliding at high displacement rates. We characterize this crossover with a simple scaling relation and show that the crossover is accompanied by a shift in the dominant energy dissipation mechanisms within the system.

JFM classification

Interfacial Flows (free surface): Capillary flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 973 , 25 October 2023 , A2
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. 1946 A study of locking phenomena in oscillators. Proc. IRE 34 (6), 351–357.CrossRefGoogle Scholar
Alghannam, M. & Juanes, R. 2020 Understanding rate effects in injection-induced earthquakes. Nat. Commun. 11 (1), 1–6.CrossRefGoogle ScholarPubMed
André, J. & Okumura, K. 2020 Capillary replacement in a tube prefilled with a viscous fluid. Langmuir 36 (37), 10952–10959.CrossRefGoogle Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739–805.CrossRefGoogle Scholar
Brace, W.F. & Byerlee, J.D. 1966 Stick–slip as a mechanism for earthquakes. Science 153 (3739), 990–992.CrossRefGoogle ScholarPubMed
Butt, H.-J., et al. 2022 Contact angle hysteresis. Curr. Opin. Colloid Interface Sci. 59, 101574.CrossRefGoogle Scholar
Cahn, J.W. & Hilliard, J.E. 2004 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.CrossRefGoogle Scholar
Chiarello, R., Panella, V., Krim, J. & Thompson, C. 1991 X-ray reflectivity and adsorption isotherm study of fractal scaling in vapor-deposited films. Phys. Rev. Lett. 67 (24), 3408.CrossRefGoogle ScholarPubMed
Cox, R.G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.CrossRefGoogle Scholar
Eley, D.D. & Pepper, D.C. 1946 A dynamical determination of adhesion tension. Trans. Faraday Soc. 42, 697–702.CrossRefGoogle Scholar
Gao, N., Geyer, F., Pilat, D.W., Wooh, S., Vollmer, D., Butt, H.-J. & Berger, R. 2018 How drops start sliding over solid surfaces. Nat. Phys. 14 (2), 191–196.CrossRefGoogle Scholar
de Gennes, P.G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena. Springer Science & Business Media.CrossRefGoogle Scholar
Golestanian, R. 2004 Moving contact lines on heterogeneous substrates. Phil. Trans. R. Soc. A 362 (1821), 1613–1623.CrossRefGoogle ScholarPubMed
Guo, S., Gao, M., Xiong, X., Wang, Y.J., Wang, X., Sheng, P. & Tong, P. 2013 Direct measurement of friction of a fluctuating contact line. Phys. Rev. Lett. 111 (2), 026101.CrossRefGoogle ScholarPubMed
Hatipogullari, M., Wylock, C., Pradas, M., Kalliadasis, S. & Colinet, P. 2019 Contact angle hysteresis in a microchannel: statics. Phys. Rev. Fluids 4 (4), 044008.CrossRefGoogle Scholar
Heinemann, N., et al. 2021 Enabling large-scale hydrogen storage in porous media – the scientific challenges. Energy Environ. Sci. 14 (2), 853–864.CrossRefGoogle Scholar
Hoffman, R.L. 1975 A study of the advancing interface. I. Interface shape in liquid–gas systems. J. Colloid Interface Sci. 50 (2), 228–241.CrossRefGoogle Scholar
Huh, C. & Scriven, L.E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35 (1), 85–101.CrossRefGoogle Scholar
Joanny, J.F. & Robbins, M.O. 1990 Motion of a contact line on a heterogeneous surface. J. Chem. Phys. 92, 3206–3212.CrossRefGoogle Scholar
Lee, C.H., Zhao, B., Abouatallah, R., Wang, R. & Bazylak, A. 2019 Compressible-gas invasion into liquid-saturated porous media: application to polymer-electrolyte-membrane electrolyzers. Phys. Rev. Appl. 11 (5), 054029.CrossRefGoogle Scholar
Levaché, B. & Bartolo, D. 2014 Revisiting the Saffman–Taylor experiment: imbibition patterns and liquid-entrainment transitions. Phys. Rev. Lett. 113 (4), 044501.CrossRefGoogle ScholarPubMed
Lindeman, C.W. & Nagel, S.R. 2023 State-and-rate friction in contact-line dynamics. Phys. Rev. E 107 (6), 065111.CrossRefGoogle ScholarPubMed
Liu, M. & Chen, X.P. 2017 Numerical study on the stick-slip motion of contact line moving on heterogeneous surfaces. Phys. Fluids 29 (8), 082102.CrossRefGoogle Scholar
MacMinn, C.W., Szulczewski, M.L. & Juanes, R. 2010 CO$_2$ migration in saline aquifers. Part 1. Capillary trapping under slope and groundwater flow. J. Fluid Mech. 662, 329–351.CrossRefGoogle Scholar
MacMinn, C.W., Szulczewski, M.L. & Juanes, R. 2011 CO$_2$ migration in saline aquifers. Part 2. Capillary and solubility trapping. J. Fluid Mech. 688, 321–351.CrossRefGoogle Scholar
Majumdar, A. & Tien, C.L. 1990 Fractal characterization and simulation of rough surfaces. Wear 136 (2), 313–327.CrossRefGoogle Scholar
Mannetje, D.J.C.M., Mugele, F. & Van Den Ende, D. 2013 Stick–slip to sliding transition of dynamic contact lines under AC electrowetting. Langmuir 29 (48), 15116–15121.CrossRefGoogle ScholarPubMed
Maugis, D. & Barquins, M. 1988 Stick-slip and peeling of adhesive tapes. In Adhesion 12 (ed. K.W. Allen), pp. 205–222. Springer Netherlands.CrossRefGoogle Scholar
Mumley, T.E., Radke, C.J. & Williams, M.C. 1986 Kinetics of liquid/liquid capillary rise: I. Experimental observations. J. Colloid Interface Sci. 109 (2), 398–412.CrossRefGoogle Scholar
Nasuno, S., Kudrolli, A., Bak, A. & Gollub, J.P. 1998 Time-resolved studies of stick-slip friction in sheared granular layers. Phys. Rev. E 58 (2), 2161–2171.CrossRefGoogle Scholar
Perrin, H., Lhermerout, R., Davitt, K., Rolley, E. & Andreotti, B. 2016 Defects at the nanoscale impact contact line motion at all scales. Phys. Rev. Lett. 116 (18), 184502.CrossRefGoogle ScholarPubMed
Primkulov, B.K., Chui, J.Y.Y., Pahlavan, A.A., MacMinn, C.W. & Juanes, R. 2020 a Characterizing dissipation in fluid–fluid displacement using constant-rate spontaneous imbibition. Phys. Rev. Lett. 125 (17), 174503.CrossRefGoogle ScholarPubMed
Primkulov, B.K., Pahlavan, A.A., Bourouiba, L., Bush, J.W.M. & Juanes, R. 2020 b Spin coating of capillary tubes. J. Fluid Mech. 886, A30.CrossRefGoogle Scholar
Qiu, Y., Xu, K., Pahlavan, A.A. & Juanes, R. 2023 Wetting transition and fluid trapping in a microfluidic fracture. Proc. Natl Acad. Sci. 120 (22), e2303515120.CrossRefGoogle Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38 (1), 71–99.CrossRefGoogle Scholar
Raphaël, E. & De Gennes, P.G. 1989 Dynamics of wetting with nonideal surfaces. The single defect problem. J. Chem. Phys. 90, 7577–7584.CrossRefGoogle Scholar
Ren, W. & Weinan, E. 2011 Contact line dynamics on heterogeneous surfaces. Phys. Fluids 23 (7), 072103.CrossRefGoogle Scholar
Rice, J.R. & Tse, S.T. 1986 Dynamic motion of a single degree of freedom system following a rate and state dependent friction law. J. Geophys. Res. 91 (B1), 521–530.CrossRefGoogle Scholar
Savva, N., Pavliotis, G.A. & Kalliadasis, S. 2011 Contact lines over random topographical substrates. Part 1. Statics. J. Fluid Mech. 672, 358–383.CrossRefGoogle Scholar
Schäffer, E. & Wong, P.-Z. 2000 Contact line dynamics near the pinning threshold: a capillary rise and fall experiment. Phys. Rev. E 61 (5), 5257–5277.CrossRefGoogle ScholarPubMed
Sinha, S., Bender, A.T., Danczyk, M., Keepseagle, K., Prather, C.A., Bray, J.M., Thrane, L.W., Seymour, J.D., Codd, S.L. & Hansen, A. 2017 Effective rheology of two-phase flow in three-dimensional porous media: experiment and simulation. Transp. Porous Media 119 (1), 77–94.CrossRefGoogle ScholarPubMed
Sinha, S., Hansen, A., Bedeaux, D. & Kjelstrup, S. 2013 Effective rheology of bubbles moving in a capillary tube. Phys. Rev. E 87 (2), 025001.CrossRefGoogle Scholar
Snoeijer, J.H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45 (1), 269–292.CrossRefGoogle Scholar
Sparrow, C. & Mandelbrot, B. 1984 The fractal geometry of nature. J. R. Stat. Soc. A (General) 147 (4), 616–618.Google Scholar
Strogatz, S.H. 2018 Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd edn. CRC.CrossRefGoogle Scholar
Szulczewski, M.L., MacMinn, C.W., Herzog, H.J. & Juanes, R. 2012 Lifetime of carbon capture and storage as a climate-change mitigation technology. Proc. Natl Acad. Sci. USA 109 (14), 5185–5189.CrossRefGoogle ScholarPubMed
Thiele, U. & Knobloch, E. 2006 a Driven drops on heterogeneous substrates: onset of sliding motion. Phys. Rev. Lett. 97 (20), 204501.CrossRefGoogle ScholarPubMed
Thiele, U. & Knobloch, E. 2006 b On the depinning of a driven drop on a heterogeneous substrate. New J. Phys. 8 (12), 313.CrossRefGoogle Scholar
Varagnolo, S., Ferraro, D., Fantinel, P., Pierno, M., Mistura, G., Amati, G., Biferale, L. & Sbragaglia, M. 2013 Stick–slip sliding of water drops on chemically heterogeneous surfaces. Phys. Rev. Lett. 111 (6), 066101.CrossRefGoogle ScholarPubMed
Voinov, O.V. 1977 Hydrodynamics of wetting. Fluid Dyn. 11 (5), 714–721.CrossRefGoogle Scholar
Walls, P.L.L., Dequidt, G. & Bird, J.C. 2016 Capillary displacement of viscous liquids. Langmuir 32 (13), 3186–3190.CrossRefGoogle ScholarPubMed
Wang, Y.J., Guo, S., Chen, H.Y. & Tong, P. 2016 Understanding contact angle hysteresis on an ambient solid surface. Phys. Rev. E 93 (5), 052802.CrossRefGoogle Scholar
Yu, T.S., Bulović, V. & Hosoi, A.E. 2013 Coarsening and solidification via solvent-annealing in thin liquid films. J. Fluid Mech. 723, 69–90.CrossRefGoogle Scholar
Zhang, Z. & Xu, X. 2022 Effective boundary conditions for dynamic contact angle hysteresis on chemically inhomogeneous surfaces. J. Fluid Mech. 935, A34.CrossRefGoogle Scholar
Zhao, B., MacMinn, C.W. & Juanes, R. 2016 Wettability control on multiphase flow in patterned microfluidics. Proc. Natl Acad. Sci. 113 (37), 10251–10256.CrossRefGoogle ScholarPubMed
Zuo, B., Zheng, F.F., Zhao, Y.R., Chen, T., Yan, Z.H., Ni, H. & Wang, X. 2012 Stick–slip phenomenon in measurements of dynamic contact angles and surface viscoelasticity of poly(styrene-b-isoprene-b-styrene) triblock copolymers. Langmuir 28 (9), 4283–4292.CrossRefGoogle ScholarPubMed

Primkulov et al. Supplementary Movie

Video shows a transition from stick--slip to steady sliding with phase-field simulation of fluid-fluid displacement in a 2D channel. The crossover occurs as the capillary number increases from 1E-4 to 3E-2. Here, a dashed line represents an axis of symmetry in the 2D channel.

Download Primkulov et al. Supplementary Movie(Video)
Video 15.7 MB