Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T09:55:04.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of an inertial squirmer in a density stratified fluid

Published online by Cambridge University Press:  22 October 2020

Rishabh V. More Open the ORCID record for Rishabh V. More [Opens in a new window]  and
Arezoo M. Ardekani Open the ORCID record for Arezoo M. Ardekani [Opens in a new window]
Rishabh V. More
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN47907, USA
Arezoo M. Ardekani*
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN47907, USA
*
†Email address for correspondence: ardekani@purdue.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the self-propulsion of an inertial swimmer in a linearly density stratified fluid using the archetypal squirmer model which self-propels by generating tangential surface waves. We quantify swimming speeds for pushers (propelled from the rear) and pullers (propelled from the front) by direct numerical solution of the Navier–Stokes equations using the finite volume method for solving the fluid flow and the distributed Lagrange multiplier method for modelling the swimmer. The simulations are performed for Reynolds numbers ($Re$) between 5 and 100 and Froude numbers ($Fr$) between 1 and 10. We find that increasing the fluid stratification strength reduces the swimming speeds of both pushers and pullers relative to their speeds in a homogeneous fluid. The increase in the buoyancy force experienced by these squirmers due to the trapping of lighter fluid in their respective recirculatory regions as they move in the heavier fluid is one of the reasons for this reduction. With increasing the stratification, the isopycnals tend to deform less, which offers resistance to the flow generated by the squirmers around them to propel themselves. This resistance increases with stratification, thus, reducing the squirmer swimming velocity. Stratification also stabilizes the flow around a puller keeping it axisymmetric even at high $Re$, thus, leading to stability which is otherwise absent in a homogeneous fluid for $Re$ greater than $O(10)$. On the contrary, a strong stratification leads to instability in the motion of pushers by making the flow around them unsteady and three-dimensional, which is otherwise steady and axisymmetric in a homogeneous fluid. A pusher is a more efficient swimmer than a puller owing to efficient convection of vorticity along its surface and downstream. Data for the mixing efficiency generated by individual squirmers explain the trends observed in the mixing produced by a swarm of squirmers.

JFM classification

Biological Fluid Dynamics: Swimming/flying Geophysical and Geological Flows: Stratified flows Biological Fluid Dynamics: Micro-organism dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 905 , 25 December 2020 , A9
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alldredge, A. L., Cowles, T. J., MacIntyre, S., Rines, J. E., Donaghay, P. L., Greenlaw, C. F., Holliday, D., Dekshenieks, M. M., Sullivan, J. M. & Zaneveld, J. R. V. 2002 Occurrence and mechanisms of formation of a dramatic thin layer of marine snow in a shallow Pacific fjord. Mar. Ecol. Prog. Ser. 233, 1–12.CrossRefGoogle Scholar
Aniszewski, W., Arrufat, T., Crialesi-Esposito, M., Dabiri, S., Fuster, D., Ling, Y., Lu, J., Malan, L., Pal, S., Scardovelli, R., et al. 2019 Parallel, robust, interface simulator (Paris).Google Scholar
Ardekani, A. M., Dabiri, S. & Rangel, R. H. 2008 Collision of multi-particle and general shape objects in a viscous fluid. J. Comput. Phys. 227 (24), 10094–10107.CrossRefGoogle Scholar
Ardekani, A. M., Doostmohammadi, A. & Desai, N. 2017 Transport of particles, drops, and small organisms in density stratified fluids. Phys. Rev. Fluids 2 (10), 100503.CrossRefGoogle Scholar
Ardekani, A. M. & Rangel, R. H. 2008 Numerical investigation of particle–particle and particle–wall collisions in a viscous fluid. J. Fluid Mech. 596, 437–466.CrossRefGoogle Scholar
Ardekani, A. & Stocker, R. 2010 Stratlets: low Reynolds number point-force solutions in a stratified fluid. Phys. Rev. Lett. 105 (8), 084502.CrossRefGoogle Scholar
Baker, R. 1978 Evolutionary Ecology of Animal Migration. Holmes & Meier Publishers.Google Scholar
Banse, K. 1964 On the vertical distribution of zooplankton in the sea. Prog. Oceanogr. 2, 53–125.CrossRefGoogle Scholar
Bayareh, M., Doostmohammadi, A., Dabiri, S. & Ardekani, A. 2013 On the rising motion of a drop in stratified fluids. Phys. Fluids 25 (10), 023029.CrossRefGoogle Scholar
Beckett, B. S. 1986 Biology: A Modern Introduction. Oxford University Press.Google Scholar
Berg, H. C. 1993 Random Walks in Biology. Princeton University Press.Google Scholar
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.CrossRefGoogle Scholar
Boyd, C. & Gradmann, D. 2002 Impact of osmolytes on buoyancy of marine phytoplankton. Mar. Biol. 141 (4), 605–618.Google Scholar
Brennen, C. & Winet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9 (1), 339–398.CrossRefGoogle Scholar
Childress, S. 1981 Mechanics of Swimming and Flying, vol. 2. Cambridge University Press.CrossRefGoogle Scholar
Chisholm, N. G. & Khair, A. S. 2018 Partial drift volume due to a self-propelled swimmer. Phys. Rev. Fluids 3 (1), 014501.CrossRefGoogle Scholar
Chisholm, N. G., Legendre, D., Lauga, E. & Khair, A. S. 2016 A squirmer across Reynolds numbers. J. Fluid Mech. 796, 233–256.CrossRefGoogle Scholar
Cloern, J. E., Cole, B. E., Wong, R. L. & Alpine, A. E. 1985 Temporal dynamics of estuarine phytoplankton: a case study of San Francisco Bay. In Temporal Dynamics of an Estuary: San Francisco Bay, pp. 153–176. Springer.CrossRefGoogle Scholar
Dandekar, R., Shaik, V. A. & Ardekani, A. M. 2019 Swimming sheet in a density-stratified fluid. J. Fluid Mech. 874, 210–234.CrossRefGoogle Scholar
Dewar, W. K., Bingham, R. J., Iverson, R., Nowacek, D. P., St Laurent, L. C. & Wiebe, P. H. 2006 Does the marine biosphere mix the ocean? J. Mar. Res. 64 (4), 541–561.CrossRefGoogle Scholar
Doostmohammadi, A., Dabiri, S. & Ardekani, A. M. 2014 A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J. Fluid Mech. 750, 5–32.CrossRefGoogle Scholar
Doostmohammadi, A., Stocker, R. & Ardekani, A. M. 2012 Low-Reynolds-number swimming at pycnoclines. Proc. Natl Acad. Sci. 109 (10), 3856–3861.CrossRefGoogle ScholarPubMed
Drescher, K., Leptos, K. C., Tuval, I., Ishikawa, T., Pedley, T. J. & Goldstein, R. E. 2009 Dancing volvox: hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102 (16), 168101.CrossRefGoogle ScholarPubMed
Gemmell, B. J., Jiang, H. & Buskey, E. J. 2015 A tale of the ciliate tail: investigation into the adaptive significance of this sub-cellular structure. Proc. R. Soc. B 282 (1812), 20150770.CrossRefGoogle ScholarPubMed
Glowinski, R., Pan, T.-W., Hesla, T. I., Joseph, D. D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.CrossRefGoogle Scholar
Guasto, J. S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.CrossRefGoogle Scholar
Harder, W. 1968 Reactions of plankton organisms to water stratification. Limnol. Oceanogr. 13 (1), 156–168.CrossRefGoogle Scholar
Hershberger, P., Rensel, J., Matter, A. & Taub, F. 1997 Vertical distribution of the chloromonad flagellate heterosigma carterae in columns: implications for bloom development. Can. J. Fisheries Aquatic Sci. 54 (10), 2228–2234.CrossRefGoogle Scholar
Hill, N. & Pedley, T. 2005 Bioconvection. Fluid Dyn. Res. 37 (1–2), 1.CrossRefGoogle Scholar
Houghton, I. A., Koseff, J. R., Monismith, S. G. & Dabiri, J. O. 2018 Vertically migrating swimmers generate aggregation-scale eddies in a stratified column. Nature 556 (7702), 497.CrossRefGoogle Scholar
Isard, S. A. & Gage, S. H. 2001 Flow of Life in the Atmosphere. Michigan State University.Google Scholar
Ishikawa, T. & Hota, M. 2006 Interaction of two swimming paramecia. J. Expl Biol. 209 (22), 4452–4463.CrossRefGoogle ScholarPubMed
Ishikawa, T. & Pedley, T. 2007 The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 588, 399–435.CrossRefGoogle Scholar
Jacobson, M. Z. & Jacobson, M. Z. 2005 Fundamentals of Atmospheric Modeling. Cambridge University Press.CrossRefGoogle Scholar
Katija, K. 2012 Biogenic inputs to ocean mixing. J. Expl Biol. 215 (6), 1040–1049.CrossRefGoogle ScholarPubMed
Katija, K. & Dabiri, J. O. 2009 A viscosity-enhanced mechanism for biogenic ocean mixing. Nature 460 (7255), 624–626.CrossRefGoogle ScholarPubMed
Khair, A. S. & Chisholm, N. G. 2014 Expansions at small Reynolds numbers for the locomotion of a spherical squirmer. Phys. Fluids 26 (1), 011902.CrossRefGoogle Scholar
Kiørboe, T., Jiang, H. & Colin, S. P. 2010 Danger of zooplankton feeding: the fluid signal generated by ambush-feeding copepods. Proc. R. Soc. B 277 (1698), 3229–3237.CrossRefGoogle ScholarPubMed
Kunze, E. 2019 Biologically generated mixing in the ocean. Annu. Rev. Mar. Sci. 11, 215–226.CrossRefGoogle ScholarPubMed
Leonard, B. P. 1979 A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Mech. Engng 19 (1), 59–98.CrossRefGoogle Scholar
Li, G.-J. & Ardekani, A. M. 2014 Hydrodynamic interaction of microswimmers near a wall. Phys. Rev. E 90 (1), 013010.CrossRefGoogle Scholar
Li, G., Ostace, A. & Ardekani, A. M. 2016 Hydrodynamic interaction of swimming organisms in an inertial regime. Phys. Rev. E 94 (5), 1–8.CrossRefGoogle Scholar
Lighthill, M. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.CrossRefGoogle Scholar
Lighthill, J. 1976 Flagellar hydrodynamics. SIAM Rev. 18 (2), 161–230.CrossRefGoogle Scholar
Liu, A. G., Mcllroy, D. & Brasier, M. D. 2010 First evidence for locomotion in the Ediacara biota from the 565 Ma Mistaken Point Formation, Newfoundland. Geology 38 (2), 123–126.CrossRefGoogle Scholar
Luo, J., Ortner, P. B., Forcucci, D. & Cummings, S. R. 2000 Diel vertical migration of zooplankton and mesopelagic fish in the Arabian sea. Deep Sea Res. II 47 (7–8), 1451–1473.CrossRefGoogle Scholar
MacIntyre, S., Alldredge, A. L. & Gotschalk, C. C. 1995 Accumulation of marines now at density discontinuities in the water column. Limnol. Oceanogr. 40 (3), 449–468.CrossRefGoogle Scholar
Magar, V., Goto, T. & Pedley, T. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56 (1), 65–91.CrossRefGoogle Scholar
More, R. & Balasubramanian, S. 2018 Mixing dynamics in double-diffusive convective stratified fluid layers. Curr. Sci. 114, 1953–1960.CrossRefGoogle Scholar
Noss, C. & Lorke, A. 2012 Zooplankton induced currents and fluxes in stratified waters. Water Q. Res. J. Canada 47 (3–4), 276–286.CrossRefGoogle Scholar
Noss, C. & Lorke, A. 2014 Direct observation of biomixing by vertically migrating zooplankton. Limnol. Oceanogr. 59 (3), 724–732.CrossRefGoogle Scholar
Pedley, T. 2016 Spherical squirmers: models for swimming micro-organisms. IMA J. Appl. Maths 81 (3), 488–521.CrossRefGoogle Scholar
Rahmani, M. & Wachs, A. 2014 Free falling and rising of spherical and angular particles. Phys. Fluids 26 (8), 083301.CrossRefGoogle Scholar
Sanders, N. & Childress, J. 1988 Ion replacement as a buoyancy mechanism in a pelagic deep-sea crustacean. J. Expl Biol. 138 (1), 333–343.Google Scholar
Sartoris, F. J., Thomas, D. N., Cornils, A. & Schiela, S. B. S. 2010 Buoyancy and diapause in antarctic copepods: the role of ammonium accumulation. Limnol. Oceanogr. 55 (5), 1860–1864.CrossRefGoogle Scholar
Shapere, A. & Wilczek, F. 1989 Efficiencies of self-propulsion at low Reynolds number. J. Fluid Mech. 198, 587–599.CrossRefGoogle Scholar
Sharma, N., Chen, Y. & Patankar, N. A. 2005 A distributed lagrange multiplier based computational method for the simulation of particulate-Stokes flow. Comput. Meth. Appl. Mech. Engng 194 (45–47), 4716–4730.CrossRefGoogle Scholar
Sherman, B. S., Webster, I. T., Jones, G. J. & Oliver, R. L. 1998 Transitions between auhcoseira and anabaena dominance in a turbid river weir pool. Limnol. Oceanogr. 43 (8), 1902–1915.CrossRefGoogle Scholar
Steinberg, D. K., Van Mooy, B. A., Buesseler, K. O., Boyd, P. W., Kobari, T. & Karl, D. M. 2008 Bacterial vs. zooplankton control of sinking particle flux in the ocean's twilight zone. Limnol. Oceanogr. 53 (4), 1327–1338.CrossRefGoogle Scholar
Thiffeault, J.-L. & Childress, S. 2010 Stirring by swimming bodies. Phys. Lett. A 374 (34), 3487–3490.CrossRefGoogle Scholar
Towns, J., Cockerill, T., Dahan, M., Foster, I., Gaither, K., Grimshaw, A., Hazlewood, V., Lathrop, S., Lifka, D., Peterson, G. D., et al. 2014 XSEDE: accelerating scientific discovery. Comput. Sci. Engng 16 (5), 62–74.CrossRefGoogle Scholar
Viličić, D., Legović, T. & Žutić, V. 1989 Vertical distribution of phytoplankton in a stratified estuary. Aquat. Sci. 51 (1), 31–46.CrossRefGoogle Scholar
Villareal, T. A. & Carpenter, E. 2003 Buoyancy regulation and the potential for vertical migration in the oceanic cyanobacterium trichodesmium. Microb. Ecol. 45 (1), 1–10.CrossRefGoogle ScholarPubMed
Visser, A. W. 2007 Biomixing of the oceans? Science 316 (5826), 838–839.CrossRefGoogle ScholarPubMed
Wagner, G. L., Young, W. R. & Lauga, E. 2014 Mixing by microorganisms in stratified fluids. J. Mar. Res. 72 (2), 47–72.CrossRefGoogle Scholar
Walsby, A. E. 1994 Gas vesicles. Microbiol. Mol. Biol. Rev. 58 (1), 94–144.Google ScholarPubMed
Wang, S. & Ardekani, A. 2012 a Inertial squirmer. Phys. Fluids 24 (10), 101902.CrossRefGoogle Scholar
Wang, S. & Ardekani, A. 2012 b Unsteady swimming of small organisms. J. Fluid Mech. 702, 286–297.CrossRefGoogle Scholar
Wang, S. & Ardekani, A. M. 2015 Biogenic mixing induced by intermediate Reynolds number swimming in stratified fluids. Sci. Rep. 5, 17448.Google ScholarPubMed
Wickramarathna, L. N., Noss, C. & Lorke, A. 2014 Hydrodynamic trails produced by Daphnia: size and energetics. PLoS One 9 (3), e92383.CrossRefGoogle ScholarPubMed
Zhu, L., Lauga, E. & Brandt, L. 2012 Self-propulsion in viscoelastic fluids: pushers vs. pullers. Phys. Fluids 24 (5), 051902.CrossRefGoogle Scholar
Supplementary material: Image

More et al. Supplementary Material

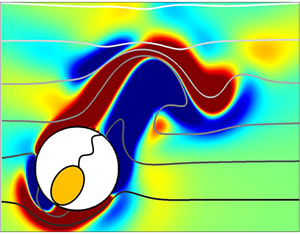
This animation depicts the effect of increasing the fluid stratification on the steady motion of a puller and a pusher with $|\beta|=3$ and $Re=50$. Increasing the stratification stabilizes a puller and destabilizes a pusher. The contours show the out of plane vorticity component. The grey lines are dimensionless isopycnal values separated by 1 unit with darker shade corresponding to a higher value

Download More et al. Supplementary Material(Image)
Image 2.4 MB