Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T16:52:04.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Natural convection in a corrugated slot

Published online by Cambridge University Press:  23 February 2017

Arman Abtahi Open the ORCID record for Arman Abtahi [Opens in a new window]  and
J. M. Floryan
Arman Abtahi*
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, N6A 5B9, Canada
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: sabtahi4@uwo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Analysis of natural convection in a horizontal slot formed by two corrugated isothermal plates has been carried out. The analysis is limited to subcritical Rayleigh numbers 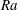$Ra$ where no secondary motion takes place in the absence of corrugations. The corrugations have a sinusoidal form characterized by the wavenumber, the upper and lower amplitudes and the phase difference. The most intense convection occurs for corrugation wavelengths comparable to the slot height; it increases proportionally to 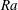$Ra$ and proportionally to the corrugation height. Placement of corrugations on both plates may either significantly increase or decrease the convection depending on the phase difference between the upper and lower corrugations, with the strongest convection found for corrugations being in phase, i.e. a ‘wavy’ slot, and the weakest for corrugations being out of phase, i.e. a ‘converging–diverging’ slot. It is shown that the shear forces would always contribute to the corrugation build-up if erosion was allowed, while the role of pressure forces depends on the location of the corrugations as well as on the corrugation height and wavenumber, and the Rayleigh number. Placing corrugations on both plates results in the formation of a moment which attempts to change the relative position of the plates. There are two limiting positions, i.e. the ‘wavy’ slot and the ‘converging–diverging’ slot, with the latter being unstable. The system would end up in the ‘wavy’ slot configuration if relative movement of the two plates was allowed. The presence of corrugations affects the conductive heat flow and creates a convective heat flow. The conductive heat flow increases with the corrugation height as well as with the corrugation wavenumber; it is largest for short-wavelength corrugations. The convective heat flow is relevant only for wavenumbers of 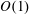$O(1)$, it increases proportionally to 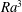$Ra^{3}$ and proportionally to the second power of the corrugation height. Convection is qualitatively similar for all Prandtl numbers 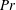$Pr$, with its intensity increasing for smaller 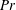$Pr$ and with the heat transfer augmentation increasing for larger 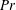$Pr$.

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 537 - 569
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abtahi, A., Hossain, M. Z. & Floryan, J. M. 2016 Spectrally accurate algorithm for analysis of convection in corrugated conduits. Comput. Maths Applics. 72, 2636–2659.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Beltrame, P., Knobloch, E., Hänggi, P. & Thiele, U. 2011 Rayleigh and depinning instabilities of forced liquid ridges on heterogeneous substrates. Phys. Rev. E 83, 016305.Google Scholar
Bénard, H. 1900 Les tourbillons cellulaires dans une nappe liquide. Revue Générale Science Pure et Applique 11, 1261–1271.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chilla, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58–82.Google ScholarPubMed
Finney, M. A., Cohen, J. D., McAllister, S. S. & Jolly, W. M. 2012 On the need for a theory of wildland fire spread. Intl J. Wildland Fire; CSIRO Publishing, doi:10.1071/WF11117.Google Scholar
Floryan, D. & Floryan, J. M. 2015 Drag reduction in heated channels. J. Fluid Mech. 765, 353–395.Google Scholar
Freund, G., Pesch, W. & Zimmermann, W. 2011 Rayleigh–Bénard convection in the presence of spatial temperature modulations. J. Fluid Mech. 673, 318–348.Google Scholar
Hossain, M. Z., Floryan, D. & Floryan, J. M. 2012 Drag reduction due to spatial thermal modulations. J. Fluid Mech. 713, 398–419.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2013a Heat transfer due to natural convection in a periodically heated slot. Trans. ASME J. Heat Transfer 135, 022503.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2013b Instabilities of natural convection in a periodically heated layer. J. Fluid Mech. 733, 33–67.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2014 Natural convection in a fluid layer periodically heated from above. Phys. Rev. E 90, 023015.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2015a Mixed convection in a periodically heated channel. J. Fluid Mech. 768, 51–90.Google Scholar
Hossain, M. Z. & Floryan, J. M. 2015b Natural convection in a horizontal fluid layer periodically heated from above and below. Phys. Rev. E 92, 02301.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Husain, S. Z. & Floryan, J. M. 2007 Immersed boundary conditions method for unsteady flow problems described by the Laplace operator. Intl J. Numer. Meth. Fluids 46, 1765–1786.Google Scholar
Husain, S. Z. & Floryan, J. M. 2010 Spectrally-accurate algorithm for moving boundary problems for the Navier–Stokes equations. J. Comput. Phys. 229, 2287–2313.Google Scholar
Krishnan, M., Ugaz, V. M. & Burns, M. A. 2002 PCR in a Rayleigh–Bénard convection cell. Science 298, 793.Google Scholar
Lenardic, A., Moresi, L., Jellinek, A. M. & Manga, M. 2005 Continental insulation, mantle cooling, and the surface area of oceans and continents. Earth Planet. Sci. Lett. 234, 317–333.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Marcq, S. & Weiss, J. 2012 Influence of sea ice lead-width distribution on turbulent heat transfer between the ocean and the atmosphere. Cryosphere 6, 143–156.Google Scholar
Maxworthy, T. 1997 Convection into domains with open boundaries. Annu. Rev. Fluid Mech. 29, 327–371.Google Scholar
McCoy, J. H., Brunner, W., Pesch, W. & Bodenschatz, E. 2008 Self-organization of topological defects due to applied constraints. Phys. Rev. Lett. 101, 254102.Google Scholar
Rayleigh, J. W. S. 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.Google Scholar
Ripesi, P., Biferale, L., Sbragaglia, M. & Wirth, A. 2014 Natural convection with mixed insulating and conducting boundary conditions: low- and high-Rayleigh-number regimes. J. Fluid Mech. 742, 636–663.Google Scholar
Rizwam, A. M., Dennis, L. Y. C. & Liu, C. 2008 A review on the generation, determination and mitigation of urban heat island. J. Environ. Sci. 20, 120–128.Google Scholar
Seiden, G., Weiss, S., McCoy, J. H., Pesch, W. & Bodenschatz, E. 2008 Pattern forming system in the presence of different symmetry-breaking mechanisms. Phys. Rev. Lett. 101, 214503.Google Scholar
Siggers, J. H., Kerswell, R. R. & Balmforth, N. J. 2004 Bounds on horizontal convection. J. Fluid Mech. 517, 55–70.CrossRefGoogle Scholar
Weiss, S., Seiden, G. & Bodenschatz, E. 2012 Pattern formation in spatially forced thermal convection. New J. Phys. 14, 053010.Google Scholar
Winters, K. B. & Young, W. R. 2009 Available potential energy and buoyancy variance in horizontal convection. J. Fluid Mech. 629, 221–230.Google Scholar