Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T06:57:03.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-field internal wave beams in two dimensions

Published online by Cambridge University Press:  31 July 2020

Bruno Voisin Open the ORCID record for Bruno Voisin [Opens in a new window]
Bruno Voisin*
Affiliation:
Laboratoire des Écoulements Géophysiques et Industriels, Université Grenoble Alpes, CNRS, Grenoble INP, 38000Grenoble, France
*
†Email address for correspondence: bruno.voisin@univ-grenoble-alpes.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

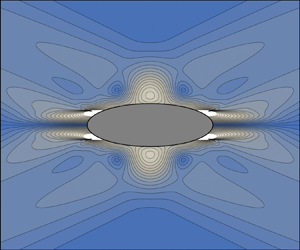
A new theory is presented for the generation of two-dimensional internal wave beams, including the effects of viscosity and unsteadiness on the propagation of the waves, and extending to the near field the classical theory of Lighthill for the far field. For this, the forcing is assumed to be of compact support. Several equivalent expressions of the waves are obtained, each associated with the choice of a support of simple shape embedding the actual support of the forcing. When the two match, the expression of the waves is valid everywhere in the fluid. For an oscillating body, the existence of critical points where the waves rays are tangential to the body is correctly accounted for, an essential requirement with regard to later inclusion of nonlinear effects and boundary layer eruption into the analysis, both of which take their origin at the critical points. Embedding supports in the shape of a circle, an ellipse and a strip are considered. Line forcing is also considered, on a weaker assumption of rapid decrease at infinity. The analysis reduces to the classical analysis of Hurley & Keady in the isotropic case of an oscillating circular cylinder, and is otherwise applied to four anisotropic oscillating bodies: an elliptic cylinder, a vertical plate, a vertical wave generator and a thin Gaussian bump.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 900 , 10 October 2020 , A3
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Appleby, J. C. & Crighton, D. G. 1986 Non-Boussinesq effects in the diffraction of internal waves from an oscillating cylinder. Q. J. Mech. Appl. Maths 39, 209–231.CrossRefGoogle Scholar
Appleby, J. C. & Crighton, D. G. 1987 Internal gravity waves generated by oscillations of a sphere. J.Fluid Mech. 183, 439–450.CrossRefGoogle Scholar
Balmforth, N. J., Ierley, G. R. & Young, W. R. 2002 Tidal conversion by subcritical topography. J. Phys. Oceanogr. 32, 2900–2914.2.0.CO;2>CrossRefGoogle Scholar
Balmforth, N. J. & Peacock, T. 2009 Tidal conversion by supercritical topography. J. Phys. Oceanogr. 39, 1965–1974.CrossRefGoogle Scholar
Bardakov, R. N., Vasil'ev, A. Y. & Chashechkin, Y. D. 2007 Calculation and measurement of conical beams of three-dimensional periodic internal waves excited by a vertically oscillating piston. Fluid Dyn. 42, 612–626.CrossRefGoogle Scholar
Beckebanze, F., Brouzet, C., Sibgatullin, I. N. & Maas, L. R. M. 2018 Damping of quasi-two-dimensional internal wave attractors by rigid-wall friction. J. Fluid Mech. 841, 614–635.CrossRefGoogle Scholar
Beckebanze, F., Raja, K. J. & Maas, L. R. M. 2019 Mean flow generation by three-dimensional nonlinear internal wave beams. J. Fluid Mech. 864, 303–326.CrossRefGoogle Scholar
Bell, T. H. 1975 a Lee waves in stratified flows with simple harmonic time dependence. J. Fluid Mech. 67, 705–722.CrossRefGoogle Scholar
Bell, T. H. 1975 b Topographically generated internal waves in the open ocean. J. Geophys. Res. 80, 320–327.CrossRefGoogle Scholar
Bigot, B., Bonometti, T., Lacaze, L. & Thual, O. 2014 A simple immersed-boundary method for solid–fluid interaction in constant- and stratified-density flows. Comput. Fluids 97, 126–142.CrossRefGoogle Scholar
Boury, S., Peacock, T. & Odier, P. 2019 Excitation and resonant enhancement of axisymmetric internal wave modes. Phys. Rev. Fluids 4, 034802.CrossRefGoogle Scholar
Brunet, M., Dauxois, T. & Cortet, P.-P. 2019 Linear and nonlinear regimes of an inertial wave attractor. Phys. Rev. Fluids 4, 034801.CrossRefGoogle Scholar
Bryan, G. H. 1889 The waves on a rotating liquid spheroid of finite ellipticity. Phil. Trans. R. Soc. Lond. A 180, 187–219.Google Scholar
Bühler, O. & Muller, C. J. 2007 Instability and focusing of internal tides in the deep ocean. J. Fluid Mech. 588, 1–28.CrossRefGoogle Scholar
Chashechkin, Y. D. 2018 Singular perturbed components of flows – linear precursors of shock waves. Math. Model. Nat. Phenom. 13, 17.CrossRefGoogle Scholar
Chashechkin, Y. D. & Kistovich, Y. V. 1997 Generation of monochromatic internal waves: an exact solution and the force-source model. Phys. Dokl. 42, 377–380.Google Scholar
Chashechkin, Y. D., Vasil'ev, A. Y. & Bardakov, R. N. 2004 Fine structure of beams of a three-dimensional periodic internal wave. Dokl. Earth Sci. 397A, 816–819.Google Scholar
Cox, C. & Sandstrom, H. 1962 Coupling of internal and surface waves in water of variable depth. J.Oceanogr. Soc. Japan 20th Anniversary Volume, 499–513.Google Scholar
Dalziel, S. B., Hughes, G. O. & Sutherland, B. R. 2000 Whole-field density measurements by ‘synthetic schlieren’. Exp. Fluids 28, 322–335.CrossRefGoogle Scholar
Dauxois, T., Joubaud, S., Odier, P. & Venaille, A. 2018 Instabilities of internal gravity wave beams. Annu. Rev. Fluid Mech. 50, 131–156.CrossRefGoogle Scholar
Davis, A. M. J. 2012 Generation of internal waves from rest: extended use of complex coordinates, for a sphere but not a disk. J. Fluid Mech. 703, 374–390.CrossRefGoogle Scholar
Davis, A. M. J. & Llewellyn Smith, S. G. 2010 Tangential oscillations of a circular disk in a viscous stratified fluid. J. Fluid Mech. 656, 342–359.CrossRefGoogle Scholar
Dobra, T. E., Lawrie, A. G. W. & Dalziel, S. B. 2019 The magic carpet: an arbitrary spectrum wave maker for internal waves. Exp. Fluids 60, 172.CrossRefGoogle Scholar
Dossmann, Y., Bourget, B., Brouzet, C., Dauxois, T., Joubaud, S. & Odier, P. 2016 Mixing by internal waves quantified using combined PIV/PLIF technique. Exp. Fluids 57, 132.CrossRefGoogle Scholar
Dossmann, Y., Pollet, F., Odier, P. & Dauxois, T. 2017 Mixing and formation of layers by internal wave forcing. J. Geophys. Res. Oceans 122, 9906–9917.CrossRefGoogle Scholar
Echeverri, P. & Peacock, T. 2010 Internal tide generation by arbitrary two-dimensional topography. J.Fluid Mech. 659, 247–266.CrossRefGoogle Scholar
Echeverri, P., Yokossi, T., Balmforth, N. J. & Peacock, T. 2011 Tidally generated internal-wave attractors between double ridges. J. Fluid Mech. 669, 354–374.CrossRefGoogle Scholar
Ermanyuk, E. V., Flór, J.-B. & Voisin, B. 2011 Spatial structure of first and higher harmonic internal waves from a horizontally oscillating sphere. J. Fluid Mech. 671, 364–383.CrossRefGoogle Scholar
Ermanyuk, E. V. & Gavrilov, N. V. 2005 Duration of transient processes in the formation of internal-wave beams. Dokl. Phys. 50, 548–550.CrossRefGoogle Scholar
Falahat, S., Nycander, J., Roquet, F. & Zarroug, M. 2014 Global calculation of tidal energy conversion into vertical normal modes. J. Phys. Oceanogr. 44, 3225–3244.CrossRefGoogle Scholar
Flynn, M. R., Onu, K. & Sutherland, B. R. 2003 Internal wave excitation by a vertically oscillating sphere. J. Fluid Mech. 494, 65–93.CrossRefGoogle Scholar
Gabov, S. A. 1985 The solution of a problem of stratified fluid dynamics and its stabilization as $t \to \infty$. USSR Comput. Maths Math. Phys. 25 (3), 47–55.CrossRefGoogle Scholar
Gabov, S. A. & Krutitskii, P. A. 1987 On the non-stationary Larsen problem. USSR Comput. Maths Math. Phys. 27 (4), 148–154.CrossRefGoogle Scholar
Gabov, S. A. & Pletner, Y. D. 1985 An initial-boundary value problem for the gravitational-gyroscopic wave equation. USSR Comput. Maths Math. Phys. 25 (6), 64–68.CrossRefGoogle Scholar
Gabov, S. A. & Pletner, Y. D. 1988 The problem of the oscillations of a flat disc in a stratified liquid. USSR Comput. Maths Math. Phys. 28 (1), 41–47.CrossRefGoogle Scholar
Gabov, S. A. & Shevtsov, P. V. 1983 Basic boundary value problems for the equation of oscillations of a stratified fluid. Sov. Maths Dokl. 27, 238–241.Google Scholar
Gabov, S. A. & Shevtsov, P. V. 1984 On a differential equation of the type of Sobolev's equation. Sov. Maths Dokl. 29, 411–414.Google Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39, 57–87.CrossRefGoogle Scholar
Ghaemsaidi, S. J. & Peacock, T. 2013 3D Stereoscopic PIV visualization of the axisymmetric conical internal wave field generated by an oscillating sphere. Exp. Fluids 54, 1454.CrossRefGoogle Scholar
Görtler, H. 1943 Über eine Schwingungserscheinung in Flüssigkeiten mit stabiler Dichteschichtung. Z.Angew. Math. Mech. 23, 65–71.CrossRefGoogle Scholar
Görtler, H. 1944 Einige Bemerkungen über Strömungen in rotierenden Flüssigkeiten. Z. Angew. Math. Mech. 24, 210–214.CrossRefGoogle Scholar
Gostiaux, L., Didelle, H., Mercier, S. & Dauxois, T. 2007 A novel internal waves generator. Exp. Fluids 42, 123–130.CrossRefGoogle Scholar
Hendershott, M. C. 1969 Impulsively started oscillations in a rotating stratified fluid. J. Fluid Mech. 36, 513–527.CrossRefGoogle Scholar
Hörmander, L. 1990 The Analysis of Linear Partial Differential Operators I, 2nd edn. Springer.Google Scholar
Hurley, D. G. 1969 The emission of internal waves by vibrating cylinders. J. Fluid Mech. 36, 657–672.CrossRefGoogle Scholar
Hurley, D. G. 1972 A general method for solving steady-state internal gravity wave problems. J. Fluid Mech. 56, 721–740.CrossRefGoogle Scholar
Hurley, D. G. 1997 The generation of internal waves by vibrating elliptic cylinders. Part 1. Inviscid solution. J. Fluid Mech. 351, 105–118.CrossRefGoogle Scholar
Hurley, D. G. & Hood, M. J. 2001 The generation of internal waves by vibrating elliptic cylinders. Part 3. Angular oscillations and comparison of theory with recent experimental observations. J. Fluid Mech. 433, 61–75.CrossRefGoogle Scholar
Hurley, D. G. & Keady, G. 1997 The generation of internal waves by vibrating elliptic cylinders. Part 2. Approximate viscous solution. J. Fluid Mech. 351, 119–138.CrossRefGoogle Scholar
Kapitonov, B. V. 1980 Potential theory for the equation of small oscillations of a rotating fluid. Maths USSR Sb. 37, 559–579.CrossRefGoogle Scholar
Kataoka, T. & Akylas, T. R. 2015 On three-dimensional internal gravity wave beams and induced large-scale mean flows. J. Fluid Mech. 769, 621–634.CrossRefGoogle Scholar
Kerswell, R. R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 98, 311–325.CrossRefGoogle Scholar
King, B., Zhang, H. P. & Swinney, H. L. 2009 Tidal flow over three-dimensional topography in a stratified fluid. Phys. Fluids 21, 116601.CrossRefGoogle Scholar
Kistovich, A. V. & Chashechkin, Y. D. 2007 Regular and singular components of periodic flows in the fluid interior. J. Appl. Maths Mech. 71, 762–771.CrossRefGoogle Scholar
Kistovich, Y. V. & Chashechkin, Y. D. 1994 Reflection of packets of internal waves from a rigid plane in a viscous fluid. Izv. Atmos. Ocean. Phys. 30, 718–724.Google Scholar
Kistovich, Y. V. & Chashechkin, Y. D. 1995 The reflection of beams of internal gravity waves at a flat rigid surface. J. Appl. Maths Mech. 59, 579–585.CrossRefGoogle Scholar
Kistovich, Y. V. & Chashechkin, Y. D. 1999 a Generation of monochromatic internal waves in a viscous fluid. J. Appl. Mech. Tech. Phys. 40, 1020–1028.Google Scholar
Kistovich, Y. V. & Chashechkin, Y. D. 1999 b An exact solution of a linearized problem of the radiation of monochromatic internal waves in a viscous fluid. J. Appl. Maths Mech. 63, 587–594.CrossRefGoogle Scholar
Korobov, A. S. & Lamb, K. G. 2008 Interharmonics in internal gravity waves generated by tide–topography interaction. J. Fluid Mech. 611, 61–95.CrossRefGoogle Scholar
Krishna, D. V. & Sarma, L. V. 1969 Motion of an axisymmetric body in a rotating stratified fluid confined between two parallel planes. J. Fluid Mech. 38, 833–842.CrossRefGoogle Scholar
Lai, R. Y. S. & Lee, C. -M. 1981 Added mass of a spheroid oscillating in a linearly stratified fluid. Intl J. Engng Sci. 19, 1411–1420.CrossRefGoogle Scholar
Le Dizès, S. 2015 Wave field and zonal flow of a librating disk. J. Fluid Mech. 782, 178–208.CrossRefGoogle Scholar
Le Dizès, S. & Le Bars, M. 2017 Internal shear layers from librating objects. J. Fluid Mech. 826, 653–675.CrossRefGoogle Scholar
Lighthill, M. J. 1958 An Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press.CrossRefGoogle Scholar
Lighthill, M. J. 1960 Studies on magneto-hydrodynamic waves and other anisotropic wave motions. Phil. Trans. R. Soc. Lond. A 252, 397–430.Google Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Lighthill, J. 1990 Emendations to a proof in the general three-dimensional theory of oscillating sources of waves. Proc. R. Soc. Lond. A 427, 31–42.Google Scholar
Llewellyn Smith, S. G. & Young, W. R. 2002 Conversion of the barotropic tide. J. Phys. Oceanogr. 32, 1554–1566.2.0.CO;2>CrossRefGoogle Scholar
Llewellyn Smith, S. G. & Young, W. R. 2003 Tidal conversion at a very steep ridge. J. Fluid Mech. 495, 175–191.CrossRefGoogle Scholar
Machicoane, N., Cortet, P.-P., Voisin, B. & Moisy, F. 2015 Influence of the multipole order of the source on the decay of an inertial wave beam in a rotating fluid. Phys. Fluids 27, 066602.CrossRefGoogle Scholar
Martin, P. A. & Llewellyn Smith, S. G. 2011 Generation of internal gravity waves by an oscillating horizontal disc. Proc. R. Soc. Lond. A 467, 3406–3423.CrossRefGoogle Scholar
Martin, P. A. & Llewellyn Smith, S. G. 2012 a Internal gravity waves, boundary integral equations and radiation conditions. Wave Motion 49, 427–444.CrossRefGoogle Scholar
Martin, P. A. & Llewellyn Smith, S. G. 2012 b Generation of internal gravity waves by an oscillating horizontal elliptical plate. SIAM J. Appl. Maths 72, 725–739.CrossRefGoogle Scholar
Maurer, P., Ghaemsaidi, S. J., Joubaud, S., Peacock, T. & Odier, P. 2017 An axisymmetric inertia-gravity wave generator. Exp. Fluids 58, 143.CrossRefGoogle Scholar
Melet, A., Nikurashin, M., Muller, C., Falahat, S., Nycander, J., Timko, P. G., Arbic, B. K. & Goff, J. A. 2013 Internal tide generation by abyssal hills using analytical theory. J. Geophys. Res. Oceans 118, 6303–6318.CrossRefGoogle Scholar
Mercier, M. J., Martinand, D., Mathur, M., Gostiaux, L., Peacock, T. & Dauxois, T. 2010 New wave generation. J. Fluid Mech. 657, 308–334.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Phil. Trans. R. Soc. Lond. A 264, 597–634.Google Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid. J. Fluid Mech. 28, 1–16.CrossRefGoogle Scholar
Musgrave, R. C., Pinkel, R., MacKinnon, J. A., Mazloff, M. R. & Young, W. R. 2016 Stratified tidal flow over a tall ridge above and below the turning latitude. J. Fluid Mech. 793, 933–957.CrossRefGoogle Scholar
Nycander, J. 2005 Generation of internal waves in the deep ocean by tides. J. Geophys. Res. 110, C10028.CrossRefGoogle Scholar
Nycander, J. 2006 Tidal generation of internal waves from a periodic array of steep ridges. J. Fluid Mech. 567, 415–432.CrossRefGoogle Scholar
Ogilvie, G. I. 2005 Wave attractors and the asymptotic dissipation rate of tidal disturbances. J. Fluid Mech. 543, 19–44.CrossRefGoogle Scholar
Oser, H. 1957 Erzwungene Schwingungen in rotierenden Flüssigkeiten. Arch. Rat. Mech. Anal. 1, 81–96.CrossRefGoogle Scholar
Oser, H. 1958 Experimentelle Untersuchung über harmonische Schwingungen in rotierenden Flüssigkeiten. Z. Angew. Math. Mech. 38, 386–391.CrossRefGoogle Scholar
Paley, R. E. A. C. & Wiener, N. 1934 Fourier Transforms in the Complex Domain. American Mathematical Society.Google Scholar
Peacock, T., Echeverri, P. & Balmforth, N. J. 2008 An experimental investigation of internal tide generation by two-dimensional topography. J. Phys. Oceanogr. 38, 235–242.CrossRefGoogle Scholar
Pétrélis, F., Llewellyn Smith, S. & Young, W. R. 2006 Tidal conversion at a submarine ridge. J.Phys. Oceanogr. 36, 1053–1071.CrossRefGoogle Scholar
Ramachandra Rao, A. & Balan, K. C. 1977 Effect of viscosity on internal waves from a source in a wall. Proc. Indian Acad. Sci. A 85, 351–366.Google Scholar
Renaud, A. & Venaille, A. 2019 Boundary streaming by internal waves. J. Fluid Mech. 858, 71–90.CrossRefGoogle Scholar
Reynolds, A. 1962 Forced oscillations in a rotating liquid (II). Z. Angew Math. Phys. 13, 561–572.CrossRefGoogle Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.CrossRefGoogle Scholar
Sarma, L. V. K. V. & Krishna, D. V. 1972 Oscillation of axisymmetric bodies in a stratified fluid. Zastosow. Matem. 13, 109–121.Google Scholar
Shmakova, N., Ermanyuk, E. & Flór, J.-B. 2017 Generation of higher harmonic internal waves by oscillating spheroids. Phys. Rev. Fluids 2, 114801.CrossRefGoogle Scholar
Sibgatullin, I. N. & Ermanyuk, E. V. 2019 Internal and inertial wave attractors: a review. J. Appl. Mech. Tech. Phys. 60, 284–302.CrossRefGoogle Scholar
Skazka, V. V. 1981 Asymptotic estimates for $t \to \infty$ of mixed problems for an equation of mathematical physics. Siber. Math. J. 22, 95–106.CrossRefGoogle Scholar
St. Laurent, L. & Garrett, C. 2002 The role of internal tides in mixing the deep ocean. J. Phys. Oceanogr. 32, 2882–2899.2.0.CO;2>CrossRefGoogle Scholar
Sturova, I. V. 2001 Oscillations of a circular cylinder in a linearly stratified fluid. Fluid Dyn. 36, 478–488.CrossRefGoogle Scholar
Sturova, I. V. 2006 Oscillations of a cylinder piercing a linearly stratified fluid layer. Fluid Dyn. 41, 619–628.CrossRefGoogle Scholar
Sturova, I. V. 2011 Hydrodynamic loads acting on an oscillating cylinder submerged in a stratified fluid with ice cover. J. Appl. Mech. Tech. Phys. 52, 415–426.CrossRefGoogle Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.CrossRefGoogle Scholar
Sutherland, B. R., Dalziel, S. B., Hughes, G. O. & Linden, P. F. 1999 Visualization and measurement of internal waves by ‘synthetic schlieren’. Part 1. Vertically oscillating cylinder. J.Fluid Mech. 390, 93–126.CrossRefGoogle Scholar
Sutherland, B. R., Flynn, M. R. & Onu, K. 2003 Schlieren visualisation and measurement of axisymmetric disturbances. Nonlinear Process. Geophys. 10, 303–309.CrossRefGoogle Scholar
Sutherland, B. R., Hughes, G. O., Dalziel, S. B. & Linden, P. F. 2000 Internal waves revisited. Dyn. Atmos. Oceans 31, 209–232.CrossRefGoogle Scholar
Sutherland, B. R. & Linden, P. F. 2002 Internal wave excitation by a vertically oscillating elliptical cylinder. Phys. Fluids 14, 721–731.CrossRefGoogle Scholar
Tabaei, A. & Akylas, T. R. 2003 Nonlinear internal gravity wave beams. J. Fluid Mech. 482, 141–161.CrossRefGoogle Scholar
Tabaei, A., Akylas, T. R. & Lamb, K. G. 2005 Nonlinear effects in reflecting and colliding internal wave beams. J. Fluid Mech. 526, 217–243.CrossRefGoogle Scholar
Thomas, N. H. & Stevenson, T. N. 1972 A similarity solution for viscous internal waves. J. Fluid Mech. 54, 495–506.CrossRefGoogle Scholar
Tilgner, A. 2000 Oscillatory shear layers in source driven flows in an unbounded rotating fluid. Phys. Fluids 12, 1101–1111.CrossRefGoogle Scholar
Vasil'ev, A. Y. & Chashechkin, Y. D. 2003 The generation of beams of three-dimensional periodic internal waves in an exponentially stratified fluid. J. Appl. Maths Mech. 67, 397–405.CrossRefGoogle Scholar
Vasil'ev, A. Y. & Chashechkin, Y. D. 2006 a Generation of beams of three-dimensional periodic internal waves by sources of various types. J. Appl. Mech. Tech. Phys. 47, 314–323.CrossRefGoogle Scholar
Vasil'ev, A. Y. & Chashechkin, Y. D. 2006 b The generation of three-dimensional internal waves and attendant boundary layers in a viscous continuously stratified fluid. Construction of an analytical solution. Fluid Dyn. 41, 949–956.CrossRefGoogle Scholar
Vasil'ev, A. Y. & Chashechkin, Y. D. 2012 Three-dimensional periodic flows of an inhomogeneous fluid in the case of oscillations of part of an inclined plane. J. Appl. Maths Mech. 76, 302–309.CrossRefGoogle Scholar
Vic, C., Naveira Garabato, A. C., Green, J. A. M., Waterhouse, A. F., Zhao, Z., Melet, A., de Lavergne, C., Buijsman, M. C. & Stephenson, G. R. 2019 Deep-ocean mixing driven by small-scale internal tides. Nature Comm. 10, 2099.CrossRefGoogle ScholarPubMed
Voisin, B. 1991 Internal wave generation in uniformly stratified fluids. Part 1. Green's function and point sources. J. Fluid Mech. 231, 439–480.CrossRefGoogle Scholar
Voisin, B. 2003 Limit states of internal wave beams. J. Fluid Mech. 496, 243–293.CrossRefGoogle Scholar
Voisin, B. 2009 Added mass in density-stratified fluids. In 19ème Congrès Français de Mécanique (ed.C.Rey, P. Bontoux & A. Chrisochoos). Available at: http://hdl.handle.net/2042/37312.Google Scholar
Voisin, B., Ermanyuk, E. V. & Flór, J.-B. 2011 Internal wave generation by oscillation of a sphere, with application to internal tides. J. Fluid Mech. 666, 308–357.CrossRefGoogle Scholar
Walton, I. C. 1975 On waves in a thin rotating spherical shell of slightly viscous fluid. Mathematika 22, 46–59.CrossRefGoogle Scholar
Westerweel, J. 1997 Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 8, 1379–1392.CrossRefGoogle Scholar
Winters, K. B. & Armi, L. 2013 The response of a continuously stratified fluid to an oscillating flow past an obstacle. J. Fluid Mech. 727, 83–118.CrossRefGoogle Scholar
Zhang, H. P., King, B. & Swinney, H. L. 2007 Experimental study of internal gravity waves generated by supercritical topography. Phys. Fluids 19, 096602.CrossRefGoogle Scholar