Article contents
A new wall function method for hypersonic laminar boundary layers
Published online by Cambridge University Press: 16 February 2024
Abstract
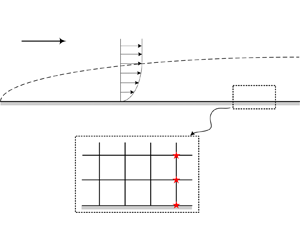
A new wall function method for hypersonic laminar boundary layers (HLBLs) is proposed to reduce the near-wall grid dependence of skin friction  $c_f$ and wall heat flux
$c_f$ and wall heat flux  $q_w$ in numerical simulations, aiming for fast and accurate predictions. First, an analytic laminar velocity law of the wall is derived, which achieves a universal scaling of the near-wall velocity of HLBLs. Then an accurate temperature–velocity relation is deduced by introducing the general recovery factor to address the invalidation of the Walz relation under the cold wall effect. Based on the laminar laws of the wall, a new wall function method for HLBLs is proposed. To avoid introducing the boundary layer edge quantities, the laminar laws of the wall are reformed by modifying the outer boundary conditions of the differential equation in deriving the temperature–velocity relation. Unlike the wall function method in turbulence, the new wall function obtains directly the accurate
$q_w$ in numerical simulations, aiming for fast and accurate predictions. First, an analytic laminar velocity law of the wall is derived, which achieves a universal scaling of the near-wall velocity of HLBLs. Then an accurate temperature–velocity relation is deduced by introducing the general recovery factor to address the invalidation of the Walz relation under the cold wall effect. Based on the laminar laws of the wall, a new wall function method for HLBLs is proposed. To avoid introducing the boundary layer edge quantities, the laminar laws of the wall are reformed by modifying the outer boundary conditions of the differential equation in deriving the temperature–velocity relation. Unlike the wall function method in turbulence, the new wall function obtains directly the accurate  $c_f$ and
$c_f$ and  $q_w$ by post-processing without being involved in the simulation iteration. The numerical experiments of a Mach 8 HLBL over the flat plate show that effectively, the new wall function can enlarge the distance of the first grid point off the wall
$q_w$ by post-processing without being involved in the simulation iteration. The numerical experiments of a Mach 8 HLBL over the flat plate show that effectively, the new wall function can enlarge the distance of the first grid point off the wall  $\Delta y_1$ from
$\Delta y_1$ from  $10^{-6}$ m to
$10^{-6}$ m to  $10^{-3}$ m, which brings a 50 times enhancement of the simulation efficiency. Meanwhile, the simulation errors of
$10^{-3}$ m, which brings a 50 times enhancement of the simulation efficiency. Meanwhile, the simulation errors of  $c_f$ and
$c_f$ and  $q_w$ of the mesh with
$q_w$ of the mesh with  $\Delta y_1=10^{-3}$ m are reduced significantly from 24.2 % and 18.5 % to 0.5 % and 0.1 %, respectively. Due to the new wall function removing the boundary layer edge quantities, success is also achieved under the curved walls.
$\Delta y_1=10^{-3}$ m are reduced significantly from 24.2 % and 18.5 % to 0.5 % and 0.1 %, respectively. Due to the new wall function removing the boundary layer edge quantities, success is also achieved under the curved walls.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 3
- Cited by


