Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T06:54:45.517Z Has data issue: false hasContentIssue false
  • English
  • Français

The nonlinear states of viscous capillary jets confined in the axial direction

Published online by Cambridge University Press:  17 November 2017

A. Martínez-Calvo ,
M. Rubio-Rubio Open the ORCID record for M. Rubio-Rubio [Opens in a new window]  and
A. Sevilla Open the ORCID record for A. Sevilla [Opens in a new window]
A. Martínez-Calvo
Affiliation:
Grupo de Mecánica de Fluidos, Departamento de Ingeniería Térmica y de Fluidos, Universidad Carlos III de Madrid, Av. Universidad 30, 28911 Leganés (Madrid), Spain
M. Rubio-Rubio
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Mecánica y Minera, Universidad de Jaén, Campus de las Lagunillas, 23071, Jaén, Spain
A. Sevilla*
Affiliation:
Grupo de Mecánica de Fluidos, Departamento de Ingeniería Térmica y de Fluidos, Universidad Carlos III de Madrid, Av. Universidad 30, 28911 Leganés (Madrid), Spain
*
†Email address for correspondence: alejandro.sevilla@uc3m.es
Get access Rights & Permissions [Opens in a new window]

Abstract

We report an experimental and theoretical study of the global stability and nonlinear dynamics of vertical jets of viscous liquid confined in the axial direction due to their impact on a bath of the same liquid. Previous works demonstrated that in the absence of axial confinement the steady liquid thread becomes unstable due to an axisymmetric global mode for values of the flow rate, 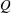$Q$, below a certain critical value, 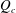$Q_{c}$, giving rise to oscillations of increasing amplitude that finally lead to a dripping regime (Sauter & Buggisch, J. Fluid Mech., vol. 533, 2005, pp. 237–257; Rubio-Rubio et al., J. Fluid Mech., vol. 729, 2013, pp. 471–483). Here we focus on the effect of the jet length, 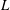$L$, on the transitions that take place for decreasing values of 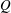$Q$. The linear stability analysis shows good agreement with our experiments, revealing that 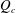$Q_{c}$ increases monotonically with 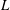$L$, reaching the semi-infinite jet asymptote for sufficiently large values of 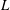$L$. Moreover, as 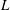$L$ decreases a quasi-static limit is reached, whereby 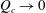$Q_{c}\rightarrow 0$ and the neutral conditions are given by a critical length determined by hydrostatics. Our experiments have also revealed the existence of a new regime intermediate between steady jetting and dripping, in which the thread reaches a limit-cycle state without breakup. We thus show that there exist three possible states depending on the values of the control parameters, namely steady jetting, oscillatory jetting and dripping. For two different combinations of liquid viscosity, $\unicode[STIX]{x1D708}$, and injector radius, 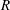$R$, the boundaries separating these regimes have been determined in the 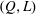$(Q,L)$ parameter plane, showing that steady jetting exists for small enough values of 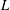$L$ or large enough values of 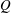$Q$, dripping prevails for small enough values of 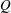$Q$ or sufficiently large values of 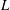$L$, and oscillatory jetting takes place in an intermediate region whose size increases with $\unicode[STIX]{x1D708}$ and decreases with 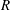$R$.

JFM classification

Instability: Absolute/convective instability Interfacial Flows (free surface): Capillary flows Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 834 , 10 January 2018 , pp. 335 - 358
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambravaneswaran, B., Subramani, H. J., Phillips, S. D. & Basaran, O. A. 2004 Dripping-jetting transitions in a dripping faucet. Phys. Rev. Lett. 93, 034501.CrossRefGoogle Scholar
Anna, S. L. 2016 Droplets and bubbles in microfluidic devices. Annu. Rev. Fluid Mech. 48, 285–309.CrossRefGoogle Scholar
Ashgriz, N. & Mashayek, F. 1995 Temporal analysis of capillary jet breakup. J. Fluid Mech. 291, 163190.CrossRefGoogle Scholar
Barrero, A. & Loscertales, I. G. 2007 Micro- and nanoparticles via capillary flows. Annu. Rev. Fluid Mech. 39, 89–106.CrossRefGoogle Scholar
Basaran, O. A. 2002 Small-scale free surface flows with breakup: drop formation and emerging applications. AIChE J. 48, 1842–1848.CrossRefGoogle Scholar
Benilov, E. S. & Cummins, C. P. 2013 The stability of a static liquid column pulled out of an infinite pool. Phys. Fluids 25, 112105.CrossRefGoogle Scholar
Benilov, E. S. & Oron, A. 2010 The height of a static liquid column pulled out of an infinite pool. Phys. Fluids 22, 102101.CrossRefGoogle Scholar
Blount, M. J. & Lister, J. R. 2011 The asymptotic structure of a slender dragged viscous thread. J. Fluid Mech. 674, 489–521.CrossRefGoogle Scholar
Bogy, D. B. 1979 Drop formation in a circular liquid jet. Annu. Rev. Fluid Mech. 11, 207–228.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2006 Spectral Methods. Fundamentals in Single Domains. Springer.CrossRefGoogle Scholar
Chiu-Webster, S. & Lister, J. R. 2006 The fall of a viscous thread onto a moving surface: a fluid-mechanical sewing machine. J. Fluid Mech. 569, 89–111.CrossRefGoogle Scholar
Christodoulides, P. & Dias, F. 2010 Impact of a falling jet. J. Fluid Mech. 657, 22–35.CrossRefGoogle Scholar
Christopher, G. F. & Anna, S. L. 2007 Microfluidic methods for generating continuous droplet streams. J. Phys. D: Appl. Phys. 40, R319–R336.CrossRefGoogle Scholar
Clanet, C. & Lasheras, J. C. 1999 Transition from dripping to jetting. J. Fluid Mech. 383, 307–326.CrossRefGoogle Scholar
Coullet, P., Mahadevan, L. & Riera, C. S. 2005 Hydrodynamical models for the chaotic dripping faucet. J. Fluid Mech. 526, 1–17.CrossRefGoogle Scholar
Derby, B. 2010 Inkjet printing of functional and structural materials: fluid property requirements, feature stability, and resolution. Annu. Rev. Mater. Res. 40, 395–414.CrossRefGoogle Scholar
Donnelly, R. J. & Glaberson, W. I. 1966 Experiments on the capillary instability of a liquid jet. Proc. R. Soc. Lond. A 290, 547–566.Google Scholar
Doshi, J. & Reneker, D. H. 1995 Electrospinning process and applications of electrospun fibers. J. Electrostat. 35 (2), 151–160.CrossRefGoogle Scholar
Eggers, J. 1993 Universal pinching of 3d axisymmetric free-surface flow. Phys. Rev. Lett. 71, 3458–3460.CrossRefGoogle ScholarPubMed
Eggers, J 1997 Nonlinear dynamics and breakup of free surface flows. Rev. Mod. Phys. 69, 865–929.CrossRefGoogle Scholar
Eggers, J. & Dupont, T. F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–222.CrossRefGoogle Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71, 036601.CrossRefGoogle Scholar
Entov, V. M. & Yarin, A. L. 1984 The dynamics of thin liquid jets in air. J. Fluid Mech. 140, 91–111.CrossRefGoogle Scholar
Evangelio, A., Campo-Cortés, F. & Gordillo, J. M. 2016 Simple and double microemulsions via the capillary breakup of highly stretched liquid jets. J. Fluid Mech. 804, 550–577.CrossRefGoogle Scholar
Gañán-Calvo, A. M. 1998 Generation of steady liquid microthreads and micron-sized monodisperse sprays in gas streams. Phys. Rev. Lett. 80 (2), 285–288.CrossRefGoogle Scholar
García, F. J. & Castellanos, A. 1994 One-dimensional models for slender axisymmetric viscous liquid jets. Phys. Fluids 6 (8), 2676–2689.CrossRefGoogle Scholar
González, H. & García, F. J. 2009 The measurement of growth rates in capillary jets. J. Fluid Mech. 619, 179–212.CrossRefGoogle Scholar
Gordillo, J. M., Sevilla, A. & Campo-Cortés, F. 2014 Global stability of stretched jets: conditions for the generation of monodisperse micro-emulsions using coflows. J. Fluid Mech. 738, 335–357.CrossRefGoogle Scholar
Guerrero, J., González, H. & García, F. J. 2016 Spatial modes in one-dimensional models for capillary jets. Phys. Rev. E 93, 033102.Google ScholarPubMed
Kalaaji, A., Lopez, B., Attane, P. & Soucemarianadin, A. 2003 Breakup length of forced liquid jets. Phys. Fluids 15, 2469–2479.CrossRefGoogle Scholar
Kovitz, A. A 1975 Static fluid interfaces external to a right circular cylinder. Experiment and theory. J. Colloid Interface Sci. 50 (1), 125–142.CrossRefGoogle Scholar
Landau, L. D. 1944 On the problem of turbulence. C.R. Acad. Sci. URSS 44, 311–314.Google Scholar
Le Dizès, S. 1997 Global modes in falling capillary jets. Eur. J. Mech. (B/Fluids) 16, 761–778.Google Scholar
Leib, S. J. & Goldstein, M. E. 1986a Convective and absolute instability of a viscous liquid jet. Phys. Fluids 29 (4), 952–954.CrossRefGoogle Scholar
Leib, S. J. & Goldstein, M. E. 1986b The generation of capillary instabilities on a liquid jet. J. Fluid Mech. 168, 479–500.CrossRefGoogle Scholar
Lin, S. P. & Reitz, R. D. 1998 Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 30, 85–105.CrossRefGoogle Scholar
Marín, A. G., Campo-Cortés, F. & Gordillo, J. M. 2009 Generation of micron-sized drops and bubbles through viscous coflows. Colloids Surf. A 344, 2–7.CrossRefGoogle Scholar
Matovich, M. A. & Pearson, J. R. A. 1969 Spinning a molten threadline. Steady-state isothermal viscous flow. Ind. Engng Chem. Fundam. 8 (3), 512–520.CrossRefGoogle Scholar
Nayfeh, A. H. 1970 Nonlinear stability of a liquid jet. Phys. Fluids 13 (4), 841–847.CrossRefGoogle Scholar
O’Donnell, B., Chen, J. N. & Lin, S. P. 2001 Transition from convective to absolute instability in a liquid jet. Phys. Fluids 13 (9), 2732–2734.CrossRefGoogle Scholar
Pearson, J. R. A. & Matovich, M. A. 1969 Spinning a molten threadline. Stability. Ind. Engng Chem. Fundam. 8 (4), 605–609.CrossRefGoogle Scholar
Plateau, J. 1873 Statique expérimentale et théorique des liquides. Gauthier–Villars et C ie .Google Scholar
Rayleigh, Lord 1878 On the instability of jets. Proc. R. Soc. Lond. A 10, 4–13.Google Scholar
Ribe, N. M., Habibi, M. & Bonn, D. 2012 Liquid rope coiling. Annu. Rev. Fluid Mech. 44, 249–266.CrossRefGoogle Scholar
Rubio-Rubio, M., Sevilla, A. & Gordillo, J. M. 2013 On the thinnest steady threads obtained by gravitational stretching of capillary jets. J. Fluid Mech. 729, 471–483.CrossRefGoogle Scholar
Rutland, D. F. & Jameson, G. J. 1971 A non-linear effect in the capillary instability of liquid jets. J. Fluid Mech. 46 (2), 267–271.CrossRefGoogle Scholar
Sauter, U. S. & Buggisch, H. W. 2005 Stability of initially slow viscous jets driven by gravity. J. Fluid Mech. 533, 237–257.CrossRefGoogle Scholar
Senchenko, S. & Bohr, T. 2005 Shape and stability of a viscous thread. Phys. Rev. E 71, 056301.Google ScholarPubMed
Sevilla, A. 2011 The effect of viscous relaxation on the spatiotemporal stability of capillary jets. J. Fluid Mech. 684, 204–226.CrossRefGoogle Scholar
Söderberg, L. D. 2003 Absolute and convective instability of a relaxational plane liquid jet. J. Fluid Mech. 493, 89–119.CrossRefGoogle Scholar
Stuart, J. T. 1958 On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 4, 1–21.CrossRefGoogle Scholar
Subramani, H. J., Yeoh, H. K., Suryo, R., Xu, Q., Ambravaneswaran, B. & Basaran, O. A. 2006 Simplicity and complexity in a dripping faucet. Phys. Fluids 18 (3), 032106.CrossRefGoogle Scholar
Suryo, R. & Basaran, O. A. 2006 Tip streaming from a liquid drop forming from a tube in a co-flowing outer fluid. Phys. Fluids 18, 082102.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Vihinen, I., Honohan, A. M. & Lin, S. P. 1997 Image of absolute instability in a liquid jet. Phys. Fluids 9 (11), 3117–3119.CrossRefGoogle Scholar
Wilkes, E. D., Phillips, S. D. & Basaran, O. A. 1999 Computational and experimental analysis of dynamics of drop formation. Phys. Fluids 11 (12), 3577–3598.CrossRefGoogle Scholar
Yuen, M.-C. 1968 Non-linear capillary instability of a liquid jet. J. Fluid Mech. 33 (1), 151–163.CrossRefGoogle Scholar

Martínez-Calvo et al. supplementary movie 1

Globally stable jet of silicone oil with a viscosity of 500 cSt injected through a needle of 3.5 mm diameter, that impinges on the free surface of a reservoir of the same liquid placed at a distance of 16.6 mm from the needle outlet. The liquid flow rate decreases smoothly from 3.6 to 3.5 ml/min, illustrating the steady jetting regime. The movie was acquired at a rate of 400 images per second, and is displayed at 60 images per second.

Download Martínez-Calvo et al. supplementary movie 1(Video)
Video 1.9 MB

Martínez-Calvo et al. supplementary movie 2

Globally unstable jet of silicone oil with a viscosity of 500 cSt injected through a needle of 3.5 mm diameter, that impinges on the free surface of a reservoir of the same liquid placed at a distance of 16.6 mm from the needle outlet. The flow rate decreases smoothly from 3.5 to 3.4 ml/min, illustrating the axisymmetric oscillatory jetting state. The movie was acquired at a rate of 400 images per second, and is displayed at 60 images per second.

Download Martínez-Calvo et al. supplementary movie 2(Video)
Video 2.2 MB

Martínez-Calvo et al. supplementary movie 3

Globally unstable jet of silicone oil with a viscosity of 500 cSt injected through a needle of 3.5 mm diameter, that impinges on the free surface of a reservoir of the same liquid placed at a distance of 16.6 mm from the needle outlet. The flow rate decreases smoothly from 3.4 to 3.3 ml/min, illustrating the transition from oscillatory jetting to dripping. The movie was acquired at a rate of 400 images per second, and is displayed at 60 images per second.

Download Martínez-Calvo et al. supplementary movie 3(Video)
Video 2.6 MB

Martínez-Calvo et al. supplementary movie 4

Numerical simulation of a globally unstable jet of silicone oil with a viscosity of 500 cSt injected through a needle of 3.5 mm diameter at a flow rate of 3.3 ml/min, impinging on the free surface of a reservoir of the same liquid placed at a distance of 16.6 mm from the needle outlet. A slight perturbation around the steady solution of the one-dimensional model is used as initial for the simulation. The movie illustrates the evolution of the jet towards the breakup of a thin filament that connects a meniscus region attached to the injector and the liquid bath. Although the subsequent dripping state established after pinch-off cannot be captured with our numerical code, the numerical evolution resembles the experiment shown in movie 3 for the same values of the control parameters.

Download Martínez-Calvo et al. supplementary movie 4(Video)
Video 4 MB

Martínez-Calvo et al. supplementary movie 5

Globally unstable jet of silicone oil with a viscosity of 1000 cSt injected through a needle of 3 mm diameter, that impinges on the free surface of a reservoir of the same liquid placed at a distance of 34.9 mm from the needle outlet. The flow rate decreases smoothly from 3.2 to 3.1 ml/min, illustrating the non-axisymmetric oscillatory jetting state with intermittent coiling. The movie was acquired at a rate of 400 images per second, and is displayed at 60 images per second.

Download Martínez-Calvo et al. supplementary movie 5(Video)
Video 1.8 MB