Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T06:36:32.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear vorticity-banding instability in granular plane Couette flow: higher-order Landau coefficients, bistability and the bifurcation scenario

Published online by Cambridge University Press:  08 February 2013

Priyanka Shukla  and
Meheboob Alam
Priyanka Shukla
Affiliation:
Department of Mathematics and Statistics, Indian Institute of Science Education and Research Kolkata, PO: BCKV Campus, Mohanpur, Nadia 741252, India Engineering Mechanics Unit, Jawaharlal Nehru Center for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Center for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
*
†Email address for correspondence: meheboob@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The rapid granular plane Couette flow is known to be unstable to pure spanwise perturbations (i.e. perturbations having variations only along the mean vorticity direction) below some critical density (volume fraction of particles), resulting in the banding of particles along the mean vorticity direction: this is dubbed ‘vorticity banding’ instability. The nonlinear state of this instability is analysed using quintic-order Landau equation that has been derived from the pertinent hydrodynamic equations of rapid granular fluid. We have found analytical solutions for related modal/harmonic equations of finite-size perturbations up to quintic order in perturbation amplitude, leading to an exact calculation of both first and second Landau coefficients. This helped to identify the bistable nature of nonlinear vorticity-banding instability for a range of densities spanning from moderately dense to dense flows. For perturbations with small spanwise wavenumbers, the bifurcation scenario for vorticity banding unfolds, with increasing density from the dilute limit, as supercritical pitchfork 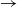$\rightarrow $ subcritical pitchfork 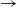$\rightarrow $ subcritical Hopf bifurcations. The transition from supercritical to subcritical pitchfork bifurcations is found to occur via the appearance of a degenerate/bicritical point (at which both the linear growth rate and the first Landau coefficient are simultaneously zero) that divides the critical line into two parts: one representing the first-order and the other the second-order phase transitions. Both subcritical oscillatory and stationary solutions have also been uncovered for dilute and dense flows, respectively, when the spanwise wavenumber is large. In all cases, the nonlinear solutions correspond to inhomogeneous states of shear stress and pressure along the vorticity direction, and hence are analogues of vorticity banding in other complex fluids. The quartic-order mean-flow resonance is evidenced in the parameter space for which the second Landau coefficient undergoes a jump discontinuity of infinite order. The importance of retaining higher-order terms to calculate the second Landau coefficient and their possible effects on the nature of bifurcations are elucidated.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Complex Fluids: Complex Fluids Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 718 , 10 March 2013 , pp. 131 - 180
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. 2005 Universal unfolding of pitchfork bifurcations and the shear-band formation in rapid granular Couette flow. In Trends in Applications of Mathematics to Mechanics (ed. Wang, Y. & Hutter, K.), pp. 11–20. Shaker.Google Scholar
Alam, M. 2006 Streamwise structures and density patterns in rapid granular Couette flow: a linear stability analysis. J. Fluid Mech. 553, 1.Google Scholar
Alam, M. 2012 Non-modal stability and optimal perturbations in unbounded granular shear flow: three-dimensionality and particle spin. Prog. Theor. Phys. Suppl. 195, 78.Google Scholar
Alam, M., Arakeri, V. H., Goddard, J. D., Nott, P. R. & Herrmann, H. J. 2005 Instability-induced ordering, universal unfolding and the role of gravity in granular Couette flow. J. Fluid Mech. 523, 277.Google Scholar
Alam, M. & Luding, S. 2003 First normal stress difference and crystallization in a dense sheared granular fluid. Phys. Fluids 15, 2298.Google Scholar
Alam, M. & Luding, S. 2005 Energy non-equipartition, rheology and micro-structure in sheared bidisperse granular mixtures. Phys. Fluids 17, 063303.Google Scholar
Alam, M. & Shukla, P. 2008 Nonlinear stability of granular shear flow: Landau equation, shear-banding and universality. In Proceedings of the International Conference on Theoretical and Applied Mechanics, August, Adelaide, Australia, pp. 24–29.Google Scholar
Alam, M. & Shukla, P. 2012 Origin of subcritical shear-banding instability in a dense two-dimensional sheared granular fluid. Granul. Matt. 14, 221.CrossRefGoogle Scholar
Alam, M. & Shukla, P. 2013 Nonlinear stability, bifurcation and vortical patterns in three-dimensional granular plane Couette flow. J. Fluid Mech. 716, 349–413.Google Scholar
Alam, M., Shukla, P. & Luding, S. 2008 Universality of shear-banding instability and crystallization in sheared granular fluid. J. Fluid Mech. 615, 293.Google Scholar
Berret, J.-F., Porte, G. & Decruppe, J.-P. 1997 Inhomogeneous shear flows of worm-like micelles: a master dynamic phase diagram. Phys. Rev. E 55, 1668.Google Scholar
Bonn, D., Meunier, J., Greffier, O., Al-Kahwaji, A. & Kellay, H. 1998 Bistability in non-Newtonian flow: rheology of lyotropic liquid crystals. Phys. Rev. E 58, 2115.CrossRefGoogle Scholar
Britton, M. M. & Callaghan, P. T. 1997 Two-phase shear band structures at uniform Stress. Phys. Rev. Lett. 78, 4930.Google Scholar
Caserta, S., Simeone, M. & Guido, S. 2008 Shear-banding in biphasic liquid–liquid systems. Phys. Rev. Lett. 100, 137801.Google Scholar
Chikkadi, V. K. & Alam, M. 2009 Slip velocity and stresses in granular Poiseuille flow via event-driven simulation. Phys. Rev. E 79, 021303.Google Scholar
Conway, S. & Glasser, B. J. 2004 Density waves and coherent structures in granular Couette flow. Phys. Fluids 16, 509.CrossRefGoogle Scholar
Dhont, J. K. G. & Briels, W. J. 2008 Gradient and vorticity banding. Rheol. Acta 47, 257.Google Scholar
Eshuis, P., van der Meer, D., Alam, M., van Gerner, H. J., van der Weele, K. & Lohse, D. 2010 Onset of convection in strongly shaken granular matter. Phys. Rev. Lett. 104, 038001.Google Scholar
Fielding, S. M. 2007 Complex dynamics of shear banded flows. Soft Matt. 3, 1262.Google Scholar
Garcia-Rojo, R., Luding, S. & Brey, J. J. 2006 Transport coefficients for dense hard-disk systems. Phys. Rev. E 74, 061305.Google Scholar
Garzo, V., Santos, A. & Montanero, J. M. 2007 Modified Sonine approximation for the Navier–Stokes transport coefficients of a granular gas. Physica A 376, 94.CrossRefGoogle Scholar
Gayen, B. & Alam, M. 2006 Algebraic and exponential instabilities in a sheared micropolar granular fluid. J. Fluid Mech. 567, 195.Google Scholar
Goddard, J. D. & Alam, M. 1999 Shear flow and material instabilities in particulate suspensions and dry granular media. Particulate Sci. Tech. 17, 69.Google Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267.Google Scholar
Grebenkov, D. S., Ciamarra, M. P., Nicodemi, M. & Coniglio, A. 2008 Flow, ordering, and jamming of sheared granular suspensions. Phys. Rev. Lett. 100, 078001.Google Scholar
Hoffman, R. L. 1972 Discontinuous and dilatant viscosity behaviour in concentrated suspensions. I. Observation of a flow instability. Trans. Soc. Rheol. 16, 155.Google Scholar
Holmes, W. M., Callaghan, P. T., Vlassopoulos, D. & Roovers, J. 2004 Shear banding phenomena in ultra-soft colloidal glasses. J. Rheol. 48, 1085.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985 Grads 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355.CrossRefGoogle Scholar
Jenkins, J. T. & Richman, M. W. 1986 Boundary conditions for plane flows of smooth, nearly elastic, circular disks. J. Fluid Mech. 171, 53.Google Scholar
Khain, E. & Meerson, B. 2006 Shear-induced crystallization of a dense rapid granular flow: Hydrodynamics beyond the melting point. Phys. Rev. E 73, 061301.Google Scholar
Lettinga, M. P. & Dhont, J. K. G. 2004 Non-equilibrium phase behaviour of rod-like viruses under shear flow. J. Phys.: Condens. Matter 16, S3929.Google Scholar
Lin-Gibson, S., Pathak, J. A., Grulke, E. A., Wang, H. & Hobbie, E. K. 2004 Elastic flow instability in nanotube suspensions. Phys. Rev. Lett. 92, 048302.Google Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. J. Fluid Mech. 140, 223.Google Scholar
Morozov, A. N. & van Saarloos, W. 2007 An introductory essay on subcritical instabilities and the transition to turbulence in visco-elastic parallel shear flows. Phys. Rep. 447, 112.CrossRefGoogle Scholar
Noskowicz, S. H., Bar-Lev, O., Serero, D. & Goldhirsch, I. 2007 Computer-aided kinetic theory and granular gases. Europhys. Lett. 79, 60001.Google Scholar
Olmsted, P. D. 2008 Perspective on shear banding in complex fluids. Rheol. Acta 47, 283.Google Scholar
Pujolle-Robic, C. & Noirez, L. 2001 Observation of shear-induced nematic–isotropic transition in side-chain liquid crystal polymers. Nature 409, 167.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465.Google Scholar
Saitoh, K. & Hayakawa, H. 2007 Rheology of a granular gas under a plane shear. Phys. Rev. E 75, 021302.CrossRefGoogle Scholar
Saitoh, K. & Hayakawa, H. 2011 Weakly nonlinear analysis of two-dimensional sheared granular flow. Granul Matt. 13, 679.Google Scholar
Salmon, J.-B., Manneville, S. & Colin, A. 2003 Shear banding in a lyotropic lamellar phase. I. Time-averaged velocity profiles. Phys. Rev. E 68, 051503.Google Scholar
Savage, S. B. & Sayed, S. 1984 Stresses developed by dry cohesion-less granular materials sheared in an annular shear cell. J. Fluid Mech. 142, 391.CrossRefGoogle Scholar
Schall, P. & van Hecke, M. 2010 Shear bands in matter with granularity. Annu. Rev. Fluid Mech. 42, 67.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid shear flows of smooth, inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41.Google Scholar
Shukla, P. & Alam, M. 2009 Order parameter description of shear-banding in granular Couette flow via Landau equation. Phys. Rev. Lett. 103, 068001.Google Scholar
Shukla, P. & Alam, M. 2011a Weakly nonlinear theory of shear-banding instability in granular plane Couette flow: analytical solution, comparison with numerics and bifurcation. J. Fluid Mech. 666, 204.Google Scholar
Shukla, P. & Alam, M. 2011b Nonlinear stability and patterns in granular plane Couette flow: Hopf and pitchfork bifurcations, and evidence for resonance. J. Fluid Mech. 672, 147.Google Scholar
Spenley, N. A., Cates, M. E. & McLeish, T. C. B. 1993 Nonlinear rheology of worm-like micelles. Phys. Rev. Lett. 71, 939.Google Scholar
Stewartson, K. & Stuart, J. T. 1971 A nonlinear stability theory for a wave system in plane Poiseuille flow. J. Fluid Mech. 48, 529.Google Scholar
Stuart, J. T. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. J. Fluid Mech. 9, 353.Google Scholar
Tan, M.-L. & Goldhirsch, I. 1997 Inter-cluster interactions in rapid granular shear flows. Phys. Fluids 9, 856.Google Scholar
Watson, J. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. J. Fluid Mech. 9, 371.Google Scholar