Article contents
Non-monotonic effect of compaction on longitudinal dispersion coefficient of porous media
Published online by Cambridge University Press: 04 June 2024
Abstract
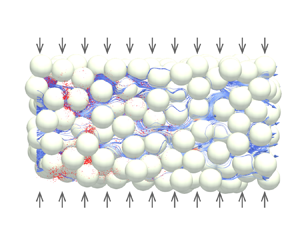
Utilizing the discrete element method and the pore network model, we numerically investigate the impact of compaction on the longitudinal dispersion coefficient of porous media. Notably, the dispersion coefficient exhibits a non-monotonic dependence on the degree of compaction, which is distinguished by the presence of three distinct regimes in the variation of dispersion coefficient. The non-monotonic variation of dispersion coefficient is attributed to the disparate effect of compaction on dispersion mechanisms. Specifically, the porous medium tightens with an increasing pressure load, reducing the effect of molecular diffusion that primarily governs at small Péclet numbers. On the other hand, heightened pressure loads enhance the heterogeneity of pore structures, resulting in increased disorder and a higher proportion of stagnant zones within porous media flow. These enhancements further strengthen mechanical dispersion and hold-up dispersion, respectively, both acting at higher Péclet numbers. It is crucial to highlight that hold-up dispersion is induced by the low-velocity regions in porous media flow, which differ fundamentally from zero-velocity regions (such as dead-ends or the interior of permeable grains) as described by the classical theory of dispersion. The competition between weakened molecular diffusion and enhanced hold-up dispersion and mechanical dispersion, together with the shift in the dominance of dispersion mechanisms across various Péclet numbers, results in multiple regimes in the variation of dispersion coefficients. Our study provides unique insights into structural design and modulation of the dispersion coefficient of porous materials.
JFM classification
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 5
- Cited by


