Non-monotonic wettability effects on displacement in heterogeneous porous media

Abstract

We report non-monotonic wettability effects on displacement efficiency in heterogeneous porous structures at the post-breakthrough stage, in contrast to the monotonic ones in homogeneous porous structures. Experiments on designed microfluidic chips show that there exists a critical wettability to attain the highest efficiency of displacement in the porous matrix structure combined with a preferential flow pathway, while a stronger wettability of the displacing fluid leads to a higher displacement efficiency on the same matrix structure only. The porous structure with or without a preferential flow pathway results in totally different topological characteristics of phase distribution during displacement. Pore-scale mechanisms are identified to elucidate the formation of this non-monotonic wettability rule: cooperative pore filling under weakly water-wet conditions yields the best displacement; corner flow under strongly water-wet conditions and Haines events under strongly oil-wet conditions decrease the displacement efficiency. The pore-scale findings may provide unique insights into the joint effects of both wettability and flow heterogeneity on fluid displacement in porous media.

1. Introduction

Multiphase displacement in porous media occurs ubiquitously in natural and industrial processes, such as geological carbon sequestration (Huppert & Neufeld 2014), hydrocarbon recovery (Lake 1989), soil remediation (Cueto-Felgueroso & Juanes 2008) and biomedical research (Sackmann, Fulton & Beebe 2014). One of the main challenges in understanding these multiphase displacement behaviours stems from the heterogeneity in hydraulic properties widely occurring in porous media (Le Goc, de Dreuzy & Davy 2010; Siena et al. 2019). For instance, in geological CO$_2$ sequestration, brine flows back to displace liquid CO$_2$ when supercritical CO$_2$ injection is terminated, and the occurrence of fingering phenomena can notably increase the storage efficiency by increasing the interfacial area and improving capillary trapping (Huppert & Neufeld 2014). In enhanced oil recovery processes, the preferential flow of the displacing fluid may result in circumvention of large areas of low-permeability reservoir matrix regions so that oil remains trapped in unswept zones (Lake 1989). Moreover, wettability conditions are also of great significance for better operations and descriptions of the efficiency and dynamics of immiscible multiphase fluid displacement in porous media. Regarding the strong wetting phase of the displacing fluid, the fluid tends to fill smaller pores or tends to flow along walls into corners to trap non-wetting fluids (Salathiel 1973; Tuller & Or 2001). However, regarding the strong wetting phase of the displaced fluid, the displacing fluid notably enters pores to occupy the pore space from the centre (Edery, Berg & Weitz 2018).

Both core- and pore-scale studies have been conducted to reveal the wettability effects on fluid–fluid displacement in porous media. Customarily for mechanism studies at such scales, without losing generality, the displacement efficiency is quantified as the displacing fluid saturation at the final steady state to characterize the displacement process. In core-scale studies, a consensus seems to have been largely reached that the displacement efficiency is a non-monotonic function of the wettability index, i.e. a critical wetting condition could occur, yielding the best displacement (Amott 1959; Morrow 1990; Jadhunandan & Morrow 1995; Al-Futaisi & Patzek 2003; Valvatne & Blunt 2004; Chen, Hirasaki & Flaum 2006; Gandomkar & Rahimpour 2015). However, it is not easy to elucidate microscale mechanisms in core flooding experiments because of the difficulty of observing and quantifying multiphase interactions (Mascini et al. 2021). In recent years, the advances of microfluidic experiments have provided us with alternative methods to conveniently observe multiphase fluid dynamics and reveal displacement mechanisms (Anbari et al. 2018).

In contrast to core-scale experiments, most pore-scale studies have indicated that a greater affinity of the invading fluid towards solid structures leads to a higher recovery or displacement efficiency (Cieplak & Robbins 1988, 1990; Holtzman & Segre 2015; Jung et al. 2016; Singh et al. 2017; Hu et al. 2019). For instance, these pore-scale displacement experiments on microchips, with either structured or random matrix geometries, have demonstrated that a lower contact angle could transform the displacement mode from ramified front displacement into compact front displacement, and a higher displacement efficiency could thus be achieved (Jung et al. 2016; Singh et al. 2017, 2019). Meanwhile, some recent interesting studies reported non-monotonic wettability effects on displacement by a new microfluidic design of circular-disc flow cells with injecting water from the centre (Trojer, Szulczewski & Juanes 2015; Zhao, MacMinn & Juanes 2016). The flow heterogeneity was remarkable by multiphase interface instability, either viscous fingering or capillary fingering, even before the breakthrough stage. It was also interesting to find that the experimental observations were consistent with the results by the modified network models (Primkulov et al. 2018, 2019, 2021), which indicated that the critical wettability for best displacement generally corresponded to the cooperative pore-filling mode.

What causes the above differences in wettability effects on the displacement efficiency? We know that fluids tend to flow along the path with the smallest resistance. As a natural consequence, the geometrical heterogeneity of porous solids, such as rocks, in natural and industrial applications leads to a preferential flow through the higher-permeability parts (Zhang et al. 2011). On the other hand, flow heterogeneity can be induced even in homogeneous porous structures by fluid–fluid interface instability, including viscous fingering and capillary fingering (Trojer et al. 2015; Zhao et al. 2016). Even if there is no fingering, asymmetrical injection may also result in preferential flows in homogeneous porous structures (Lake 1989; Zhao et al. 2016; Xie et al. 2021). Therefore, flow heterogeneity due to the existence of preferential flow may yield significant effects on mechanism analysis in terms of microfluidic experiments and pore-scale simulations, especially after the breakthrough stage, which seems to have been ignored in previous pore-scale studies.

Here, we shall reveal the wettability effects on multiphase displacement on microfluidic chips with heterogeneous microstructures. A preferential flow pathway (PFP) is artificially designed on microchips to lead to controllable flow heterogeneity, on which a series of experiments will be performed and compared with homogeneous porous structures under various wetting conditions. The underlying mechanisms are analysed based on phase distribution patterns, multiphase interactions and dynamic mode transformations. Our results demonstrate that flow heterogeneity can endow non-monotonic wettability effects, which impact the microscale physics and macroscopic consequences of multiphase displacement.

2. Experimental and analytical methods

In most previous displacement experiments on microchips, a homogeneous porous structure with a piston-type injection method was applied, which may probably be the reason that has led to monotonic wettability effects on displacement. In this work, we focus on the multiphase displacement mechanisms in porous media with flow heterogeneity, caused by either geometrical heterogeneity or flow instability. To make the experiments controllable and repeatable, we design a porous microstructure actively containing a high-permeability layer to generate a PFP on the microfluidic chip. Experiments are performed on this heterogeneous structure, and compared with the displacement process in the same matrix structure without PFP (see figure 1a). The porosities of the PFP region and the matrix region are the same ($\phi = 0.45$), while the permeability ratio between these two regions is around 16 : 1 by three-dimensional (3-D) lattice Boltzmann simulations. The pore volumes of PFP and matrix region are 0.15 $\mathrm {\mu }$l and 0.84 $\mathrm {\mu }$l, respectively, and the pore size ranges from 1.5 $\mathrm {\mu }$m to 70 $\mathrm {\mu }$m (figure 1b). The design method of the matrix region is almost the same as that presented by Lei et al. (2020) to reflect the statistical natural porous structure information. The microfluidic chips were created from a silicon wafer via microfabrication techniques (Chomsurin & Werth 2003).

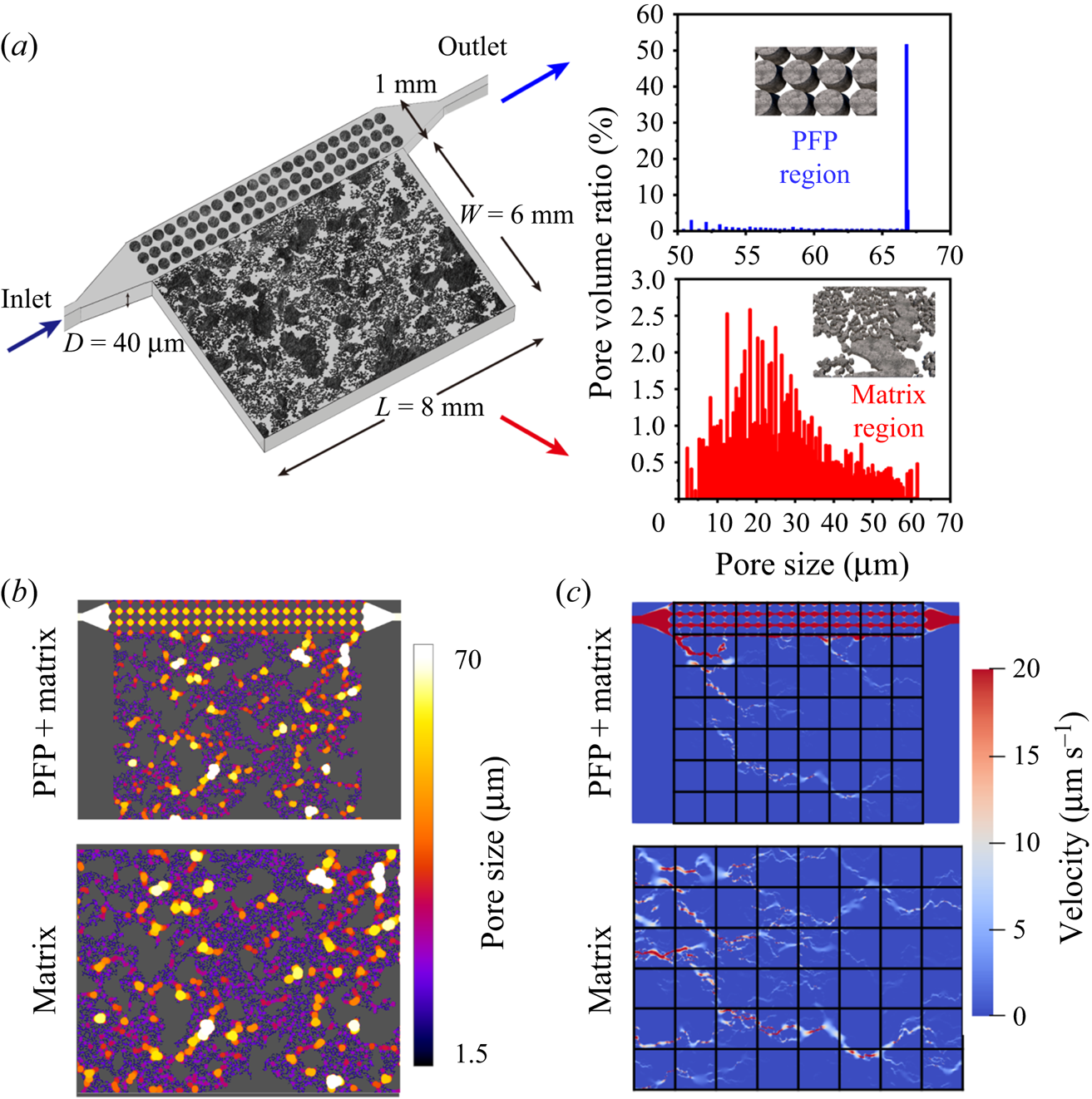
Figure 1. Microchip designs of heterogeneous porous media. (a) Microchip design of porous media containing PFP and matrix regions based on the corresponding pore-size distribution in rocks (see Lei et al. 2020). (b) The 3-D pore-size spatial distribution, ranging from 1.5 to 70 $\mathrm {\mu }$m. (c) Typical flow patterns on the homogeneous (matrix-only) and heterogeneous (${\rm PFP}+{\rm matrix}$) structures.

Five invading fluids have been prepared with similar viscosities $\mathrm {\mu }$ and interfacial tensions $\sigma$. The surfactant solution of Sulfobetaine 12 (S12; Macklin) was prepared to adjust the contact angle $\theta$ primarily. NES (Nano-Emulsion with Surfactant, 10 vol.$\%$ Span, 5 vol.$\%$ Tween, 60 vol.$\%$ mineral oil and 25 vol.$\%$ DI water) was a new solution made by our laboratory to combine with S12 to further reduce the contact angle. Finally, we can obtain characteristic contact angles varying from $\theta \approx 20^\circ$ (strongly water-wet, 0.2 wt.$\%$ S12 $+$ 3 vol.$\%$ NES), $\theta \approx 45^\circ$ (moderately water-wet, 0.2 wt.$\%$ S12 $+$ 1 vol.$\%$ NES), $\theta \approx 65^\circ$ (weakly water-wet, 0.2 wt.$\%$ S12) and $\theta \approx 90^\circ$ (neutral, 0.1 wt.$\%$ S12) to $\theta \approx 120^\circ$ (oil-wet, 0.05 wt.$\%$ S12).

The defending fluid in displacements was fluorescent dyed oil (100 ppm Nile red in decane, with dynamic viscosity $\mu _{def} = 0.838\ {\rm mPa}\ {\rm s}$), which was injected until all pores of the microfluidic chip were filled. Then, the invading fluid (dynamic viscosity ${{\mu }_{inv}}=1.1\text {--}1.2\ {\rm mPa}\ {\rm s}$, and mobility ratio ${M\equiv {{{\mu }_{inv}}}/{{{\mu }_{def}}}=1.3\text {--}1.4}$ was injected to initiate the displacement experiments. The experiments were performed under a constant capillary number ${Ca\equiv {{{\mu }_{inv}}{{u}_{i}}}/{\sigma }=2.1\times {{10}^{-5}}}$, where ${u_{i}} = {LQ/V}$ is the characteristic velocity, with $L$ the length of the microchip in the flow direction, $Q$ the injection flow rate and $V$ the pore volume of the microchip. The total injected fluid volume in each experiment reached approximately 200 pore volumes to ensure a final constant phase saturation.

To quantify the fluid distribution and displacement process, the fluid topology has been characterized via the Euler number, i.e. $\chi ={{\beta }_{0}}-{{\beta }_{1}}+{{\beta }_{2}}$ (where ${{\beta }_{0}}$ is the number of objects, ${{\beta }_{1}}$ is the number of redundant loops and ${{\beta }_{2}}$ is the number of cavities ignored in the experiments), and the circularity or shape factor $c=4{\rm \pi} {A}/{{{p}^{2}}}$ (where $A$ is the ganglion area and $p$ is the ganglion perimeter). They were adopted to classify the morphology type of the residual oil, including droplets ($\chi =1$ and $0.5< c\le 1$), columns ($\chi =1$ and $0< c\le 0.5$) and clusters ($\chi <1$).

3. Results and discussion

A series of displacement experiments are performed on porous structures with PFP (PFP-type microchips), and the results are compared to those obtained in experiments under the same conditions on the same porous matrix structures only (MS-type microchips), as shown in figure 2. The evolution of the oil saturation $S$ (the displaced phase) curve for the PFP-type microfluidic chips is more sensitive to wettability alteration than that for the MS-type microfluidic chips, as shown in figure 2(k) and 2(l). The displacing fluid saturation at the breakthrough stage is defined as ${{S}_{d}} = ({{{S}_{0}}-{{S}_{b}}})/{{{S}_{0}}}$, where $S_0$ is the initial oil saturation and $S_b$ is the oil saturation at the breakthrough stage. The results at the breakthrough stage are shown in figure 2(m), which reveals that the displacing fluid saturation ($S_d$) decreases monotonically with the contact angle for both the PFP-type and MS-type microfluidic chips.

Figure 2. Wettability effects on the phase distribution, saturation and displacement efficiency. Representative displacing and displaced phase distributions in the PFP-type (a–e) and MS-type ( f–j) microfluidic chips. Evolution of the oil saturation with the pore volumes (PV) for the PFP-type (k) and MS-type (l) porous structures. Variation in the oil saturation versus the contact angle $\theta$ for the PFP- and MS-type microfluidic chips at the breakthrough stage (m) and final (post-breakthrough) stage (n). The $x$-axis error bar is generated from the contact angle measurements and the $y$-axis error bar is generated from the three repeated displacement experiments in each condition.

The displacement efficiency is defined as the displacing fluid saturation at final steady state ${{E}_{d}} = ({{{S}_{0}}-{{S}_{f}}})/{{{S}_{0}}}$, where $S_f$ is the oil saturation at the final stage, and its dependence on the contact angle $\theta$ is shown in figure 2(n). Notably, the displacement efficiency for the PFP-type structures increases with decreasing contact angle at large contact angles, which agrees with expectations, but, surprisingly, the displacement efficiency decreases with decreasing contact angle above the critical contact angle. The maximum displacement efficiency is achieved under weakly water-wet conditions. This non-monotonic wettability effect differs from that in most experiments on microfluidic chips (Jung et al. 2016; Singh et al. 2017; Hu et al. 2019) but is consistent with previous core or reservoir measurements (Amott 1959; Morrow 1990; Jadhunandan & Morrow 1995; Al-Futaisi & Patzek 2003; Valvatne & Blunt 2004; Chen et al. 2006). Furthermore, this result indicates that the wettability effect on the displacing fluid saturation can transform from monotonic at breakthrough to non-monotonic patterns at the final stage, which further agrees with core or reservoir experience (Lake 1989; Christensen & Tanino 2017). It is worth noting that the displacement process mainly occurs in the PFP part before breakthrough, and this time interval is very short (less than 0.1 ${\%}$ of the whole process). The interfacial instability is negligible, which means that neither viscous fingering (viscosity ratio $\approx 1$) nor capillary fingering will happen in the PFP part.

In natural and engineering applications, PFPs occur naturally and suffer from many flooding fluids, so the displacement process may be more efficient under weakly water-wet conditions. However, strong flow heterogeneity is usually hardly achieved via piston-type injection in most pore-scale studies, such as single-layer glass-bead-packed models (Singh et al. 2017), etched or printed microfluidic chips (Jung et al. 2016; Hu et al. 2019; Wolf, Siebert & Surmas 2020) or very small core plugs (Bakhshian et al. 2020), and the conclusion that a higher displacement efficiency of flooding can be achieved under strongly water-wet conditions is logical and reasonable. Our results highlight the importance of flow heterogeneity on wettability effect trends and may provide a possible explanation for the contradiction between pore- and core-scale studies in regard to monotonic or non-monotonic wettability effects.

The phase interaction details in pores strongly control the multiphase displacement consequences. By colouring the adopted fluids and quantifying the topology of the various phases, each ganglion is identified and classified as a droplet, column or cluster (figure 3). In the PFP-type microfluidic chips, a large number of droplets and columns are generated and trapped in the pore space under strongly water-wet conditions (figure 3a), while, under strongly oil-wet conditions, a large volume of residual clusters is retained in the deep matrix region (figure 3e). Weakly water-wet conditions yield a good mediating effect in which oil can be recovered without many trapped ganglia under a deep invasion pattern (figure 3c). In contrast, the multiphase distribution features change little for displacing and displaced fluid with wettability alteration in the MS-type microfluidic chips (figure 3f–j).

Figure 3. Displaced phase distribution and topology analysis. Ganglion identification and classification of the droplets, columns and clusters in the PFP-type (a–e, $a'\text {--}e'$) and MS-type ( f–j, $f'\text {--}j'$) microfluidic chips. Two typical metrics are considered: the difference in the volume fraction of the largest cluster (k) and isolated ganglia between the PFP- and MS-type microfluidic chips, and the corresponding relationship between these two volume fractions and the contact angle $\theta$ (k,l).

The largest oil cluster at the final stage mainly represents the residual oil not swept by the displacing fluid, while the isolated ganglia (droplets and columns) represent the oil detached from the solid structures by the invading fluid but not produced. The volume fractions of the largest oil clusters for the two microfluidic chips in the matrix regions are shown in figure 3(k), which indicates that there are large amounts of unswept residual oil in the oil-wet cases involving the PFP-type microfluidic chips, and little unswept residual oil remains in all wettability cases involving the MS-type microfluidic chips. Figure 3(l) shows the volume fractions of the isolated ganglia at the different contact angles $\theta$ for the PFP- or MS-type microfluidic chips. These results indicate that decreasing the contact angle of the invading fluid remarkably promotes ganglia flow in the PFP-type microfluidic chips but yields negligible effects on the volume fraction of the isolated ganglia in the MS-type microfluidic chips.

Based on these topological descriptions, we can illustrate that a stronger water-wet condition leads to a stronger sweeping ability in PFP-type microchips, as shown in figure 3(k). The sweeping ability characterizes the ability to influence the distribution of displaced fluid by the displacing one. Owing to the strong sweeping ability, more isolated ganglia will be generated, as shown in figure 3(l). In contrast, wettability contributes almost the same to displacement in the MS-type microchips and achieves a wide sweep area, thus a high volume fraction of isolated ganglia appears for all wettability conditions, as shown in figure 3(k) and 3(l). Combining these results with the monotonic and non-monotonic wettability effects in figure 2(n), it can be elucidated that the best displacement efficiency does not correspond to the highest sweeping ability. Another important factor, namely the carrying ability that characterizes the ability to drive the peeled-off ganglia out from the pores by the displacing fluid, may play an important role for displacement efficiency.

It is useful to define the appropriate statistical indicators to elucidate the pore-scale formation mechanism of this non-monotonic wettability rule. The characteristic displacing velocity ${{{v}_{d}}=( V\partial S/\partial t)/( L\phi D )}$ in the matrix region of PFP-type microfluidic chips represents the mean velocity (Darcy velocity) of fluid transport from the PFP region to the matrix region, where $S$ is the oil saturation, $V$ is the volume of the PFP-type microfluidic chip, $t$ is the displacing time, $L$ is the length of the matrix region, $\phi$ is the porosity and $D$ is the depth of the chips. The characteristic displacing velocity in the MS-type microfluidic chips is ${{{v}_{d}}={{{Q}_{i}}}/{( W{{\phi }_{w}}D )}}$, where $Q_i$ is the injection flow rate, $W$ is the width of the chips and $\phi _{w}$ is the porosity of the chip occupied by the displacing fluid after the breakthrough stage. The characteristic water flow velocity ${{v}_{wf}}={{\rm \Delta} {{V}_{wf}}}/({N{{A}_{cor}}}{{\rm \Delta} t})$ is calculated based on local water film generation phenomena from the beginning of water film growth to the connection of adjacent channels, where ${N}$ is the number of channels surrounding the local pore space for corner flow and ${A}_{cor}=( 1-{{\rm \pi} /4 }){{R}^{2}}$ is the corner area of the single channel, with $R$ the core flow meniscus curvature diameter, ${R={{D}_{h}}{[ \cos \theta -\sqrt {( {\rm \pi}/4\ -\theta )+\sin \theta \cos \theta } ]}/{[ ( \theta -{\rm \pi} /4 )+{{( \cos \theta )}^{2}}-\sin \theta \cos \theta ]}}$ (Dong & Chatzis 1995) and ${{D}_{h}}$ the hydraulic diameter of the channel. In the above, ${{\rm \Delta} {{V}_{wf}}}$ is the invading fluid volume difference during water film evolution from disconnected water to connected water phase in the local pore space. The local Haines event velocity is ${{v}_{H}}={{\rm \Delta} {{V}_{H}}}/({\sum {{A}_{cha}}}{{\rm \Delta} t})$, where ${\rm \Delta} {{V}_{H}}$ is the water volume difference in the local pore space during Haines events, and $\sum {{A}_{cha}}$ is the sum of the channel cross-sectional areas surrounding the local pore space during Haines events.

The pore-scale physics behind this non-monotonic wettability effect in the PFP-type microfluidic chips is controlled by the sweeping ability and carrying ability of the displacing fluid. Different transport modes (corner flow, cooperative pore filling and Haines events) are summarized to elucidate pore-scale physics under three typical wettability conditions, as drawn in figure 4.

Figure 4. Pore-scale fluid–fluid displacement topology and mechanism analysis in heterogeneous porous structures. (a) Snap-off phenomenon induced by corner flow under strongly water-wet conditions. The displaced fluid (oil), invading fluid and porous solid are represented by yellow, black and grey, respectively. (b) The competition between the characteristic displacing velocities and water film velocities in the matrix region of the PFP-type microchips and MS-type microchips. (c) Interface development through cooperative pore filling under weakly water-wet conditions. (d) The Euler number of the invading fluid changes with the injected pore volumes and the corresponding displacing fluid pattern at the final stage. (e) The evolution of Haines events under strongly oil-wet conditions. ( f) Haines event and characteristic displacing velocities in the matrix region of the PFP-type microchips.

Under strongly water-wet conditions, the macroscopic manifestation of corner flow entails the formation of isolated ganglia, and snap-off phenomena occur in the deep matrix region relatively far from the preferential flow region, as shown in figures 3(a), 3($a'$) and 4(a). The formation process of locally isolated ganglia indicates that the invading fluid traverses along with pores in a thin-film form covering the concave surfaces of pores, thereby isolating the displaced fluid before the arrival of the main fluid–fluid meniscus. The competition between the characteristic displacing velocities and water film velocities determines whether corner flow dominates the displacement process. In PFP-type microchips, corner flow is overwhelmed at the breakthrough stage but is gradually dominated after the breakthrough stage (figure 4b). In the deep matrix region of PFP-type microfluidic chips, the characteristic displacing velocity decreases to an ultra-low value, water film flow prevails and the snap-off process occurs, as shown in figure 4(a). Therefore, the snap-off process commonly occurs at the late displacement stage.

When the characteristic displacing velocity is higher than the water film velocity, as observed in our MS-type microfluidic chip experiments, corner flow becomes always increasingly overwhelmed. A large volume fraction of isolated ganglia were created by snap-off and trapped in the matrix region of PFP-type microchips, where the carrying ability is weak due to the Jamin effect of these ganglia and the ultra-low displacing velocity (pressure). Compared with the strong sweeping ability achieved in strongly water-wet conditions, the weak carrying ability of the displacing fluid will decrease the efficiency of the displacement conversely.

As the wettability varies to weakly water-wet conditions, the carrying ability of the displacing fluid will be enhanced. The fluid invasion type at the different scales changes from two-meniscus and multi-interface merging into multi-cluster merging, which is an attribute of the cooperative pore-filling mechanism (Holtzman & Segre 2015), as shown in figure 4(c). In other words, the cooperative filling process of neighbouring pores or clusters leads to a uniform and connected invasion pattern to achieve the best displacement. Hence, the Euler characteristic $\chi$ of the invading phase is considered to quantify the connectivity of the invasion pattern, as shown in figure 4(d). A lower contact angle can enhance the sweeping ability and lead to a smaller Euler number at the early stage, but this effect will be limited at the late stage due to the corner flow mode with weak carrying ability (figure 4d). The continuous decrease in the Euler number with the pore volume under weakly water-wet conditions indicates the formation of a single complex network pattern through cooperative pore filling during the invasion process. Therefore, a more profound cooperative pore-filling effect under weakly water-wet conditions results in higher efficiency of displacement.

As the wettability varies from weakly water-wet conditions to oil-wet conditions, the sweeping ability of the displacing fluid will be weakened. The burst mechanism, also referred to as Haines events (Berg et al. 2013), predominates under strongly oil-wet conditions, decreasing the displacement efficiency at a large contact angle. Haines jump events occur in several pores connected with small throats in the PFP-type microfluidic chips, as shown in figure 4(e). Once the applied pressure exceeds the threshold capillary pressure, the fluid–fluid interface tends to quickly occupy the larger pores until it reaches an equilibrium position due to the local energy barrier at the adjacent small throats. By comparing the characteristic displacing velocity to the local Haines event velocity, we find that the local Haines velocity is higher than the characteristic displacing velocity during the Haines jump and eventually stabilizes after Haines jump events because of the interfacial resistance (figure 4f). It is difficult to inject the invading fluid deep into the matrix space only by the pressure difference achieved under the occurrence of preferential flow, and the energy barrier after the Haines jump further inhibits fluid invasion. However, in the MS-type microfluidic experiments, the relatively high displacing velocity will lead to strong sweeping ability and carrying ability in all wettability condition.

Based on these pore-scale mechanism analyses, we can summarize that a stronger water-wet condition can lead to a stronger sweeping ability, while it will induce a weaker carrying ability conversely in the matrix region of PFP-type microfluidic chips. The synergistic balance between sweeping ability and carrying ability of the displacing fluid results in the highest displacement efficiency in the matrix region of the PFP-type geometries. The three typical transport modes (corner flow, cooperative pore filling and Haines events) proposed by the previous studies have been used in this work by topological statistics to quantify the impact of sweeping ability and carrying ability on displacement. In contrast, a monotonic wettability effect has been observed in the MS-type microfluidic chips, because both the sweeping ability and carrying ability for this piston-type injection design are at nearly the same high level for all wettability conditions, and a stronger wettability leads to a slightly higher sweeping ability.

4. Conclusion

In summary, we report a non-monotonic wettability effect on the displacement efficiency in heterogeneous porous media by microfluidic experiments. With a designed porous microstructure containing a preferential flow pathway (PFP), the multiphase displacement experiments show a non-monotonic wettability effect, so that the best displacement is attained under a weakly water-wet condition. The homogeneous or heterogeneous porous structures lead to totally different topological characteristics of phase distributions.

Pore-scale physics analysis further elucidates the formation of such a non-monotonic wettability effect: (1) The cooperative pore-filling effect dominates the displacement process under weakly water-wet conditions. A larger swept area and fewer trapped ganglia lead to the highest recovery or displacement efficiency. (2) Under strongly water-wet conditions, the displacement process is controlled by corner flow. With cumulative injection volume, a relatively higher corner flow velocity in the deep matrix region may frequently cause snap-off phenomena and increase the number of trapped droplets to decrease recovery or displacement efficiency. (3) Under strongly oil-wet conditions, the flow process relies on the areal sweeping ability. At a larger contact angle, the displacing phase is inhibited from propagating from the PFP into the matrix region, mainly due to Haines events.

Our microfluidics study paves the way for a better description and operations of the wettability impact on multiphase flow in many applications. However, it should be noted that the geometrical heterogeneity or injection methods will influence the flow heterogeneity, which is one of the most important factors. Accurate critical wettability conditions could be considered more under varying capillary numbers, surface roughness values and viscosity mismatch levels. All those problems will be analysed in future work. Regardless, the conclusion that the flow heterogeneity-induced non-monotonic wettability effect on displacement in porous media is applicable to multiphase behaviour in underground aquifers, hydrocarbon reservoirs, fuel cell systems and the deep stratum for CO$_2$ storage hydrocarbon reservoirs.