Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T08:48:28.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Newtonian stress, collisional dissipation and heat flux in the shear flow of inelastic disks: a reduction via Grad’s moment method

Published online by Cambridge University Press:  19 September 2014

Saikat Saha  and
Meheboob Alam
Saikat Saha
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
*
†Email address for correspondence: meheboob@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The non-Newtonian stress tensor, collisional dissipation rate and heat flux in the plane shear flow of smooth inelastic disks are analysed from the Grad-level moment equations using the anisotropic Gaussian as a reference. For steady uniform shear flow, the balance equation for the second moment of velocity fluctuations is solved semi-analytically, yielding closed-form expressions for the shear viscosity 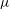$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu $, pressure 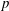$p$, first normal stress difference 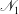${\mathcal{N}}_1$ and dissipation rate 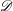${\mathcal{D}}$ as functions of (i) density or area fraction $\nu $, (ii) restitution coefficient $e$, (iii) dimensionless shear rate $R$, (iv) temperature anisotropy 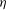$\eta $ (the difference between the principal eigenvalues of the second-moment tensor) and (v) angle 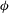$\phi $ between the principal directions of the shear tensor and the second-moment tensor. The last two parameters are zero at the Navier–Stokes order, recovering the known exact transport coefficients from the present analysis in the limit 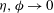$\eta ,\phi \to 0$, and are therefore measures of the non-Newtonian rheology of the medium. An exact analytical solution for leading-order moment equations is given, which helped to determine the scaling relations of 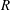$R$, 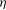$\eta $ and 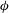$\phi $ with inelasticity. We show that the terms at super-Burnett order must be retained for a quantitative prediction of transport coefficients, especially at moderate to large densities for small values of the restitution coefficient (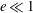$e \ll 1$). Particle simulation data for a sheared inelastic hard-disk system are compared with theoretical results, with good agreement for 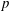$p$, 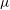$\mu $ and 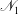${\mathcal{N}}_1$ over a range of densities spanning from the dilute to close to the freezing point. In contrast, the predictions from a constitutive model at Navier–Stokes order are found to deviate significantly from both the simulation and the moment theory even at moderate values of the restitution coefficient (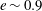$e\sim 0.9$). Lastly, a generalized Fourier law for the granular heat flux, which vanishes identically in the uniform shear state, is derived for a dilute granular gas by analysing the non-uniform shear flow via an expansion around the anisotropic Gaussian state. We show that the gradient of the deviatoric part of the kinetic stress drives a heat current and the thermal conductivity is characterized by an anisotropic second-rank tensor, for which explicit analytical expressions are given.

JFM classification

Granular media: Granular media Rarefied Gas Flow: Kinetic theory Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 251 - 296
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Luding, S. 2003a First normal stress difference and crystallization in sheared granular fluid. Phys. Fluids 15, 2298–2312.CrossRefGoogle Scholar
Alam, M. & Luding, S. 2003b Rheology of bidisperse granular mixtures via event-driven simulations. J. Fluid Mech. 476, 69–103.CrossRefGoogle Scholar
Alam, M. & Luding, S. 2005a Energy non-equipartition, rheology and microstructure in sheared bidisperse granular mixtures. Phys. Fluids 17, 063303.CrossRefGoogle Scholar
Alam, M. & Luding, S. 2005b Non-Newtonian granular fluid: simulation and theory. In Powders and Grains (ed. Garcia-Rojo, R., Herrmann, H. J. & McNamara, S.), pp. 1141–1144. A. A. Balkema.Google Scholar
Alam, M., Willits, J. T., Arnarson, B. O. & Luding, S. 2002 Kinetic theory of a binary mixture of nearly elastic disks with size and mass disparity. Phys. Fluids 14, 4085–4087.CrossRefGoogle Scholar
Araki, S. & Tremaine, S. 1986 The dynamics of dense particle disks. Icarus 65, 83–109.Google Scholar
Brey, J. J., Dufty, J. W., Kim, C. S. & Santos, A. 1998 Hydrodynamics for granular flow at low density. Phys. Rev. E 58, 4638–4653.Google Scholar
Brilliantov, N. V. & Pöschel, T. 2003 Hydrodynamics and transport coefficients for dilute granular gases. Phys. Rev. E 67, 061304.Google Scholar
Brilliantov, N. V. & Pöschel, T. 2004 Kinetic Theory of Granular Gases. Oxford University Press.Google Scholar
Burnett, D. 1935 The distribution of velocities in a slightly non-uniform gas. Proc. Lond. Math. Soc. 39, 385–430.CrossRefGoogle Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory for Non-Uniform Gases. Cambridge University Press.Google Scholar
Chou, C. S. & Richman, M. W. 1998 Constitutive theory for homogeneous granular shear flows of highly inelastic spheres. Physica A 259, 430–448.CrossRefGoogle Scholar
Esposito, L. 2006 Planetary Rings. Cambridge University Press.Google Scholar
Garzo, V. 2012 Grad’s moment method for a low density granular gas: Navier–Stokes transport coefficients. AIP Conf. Proc. 1501, 1031–1037.Google Scholar
Garzo, V., Santos, A. & Montanero, J. M. 2007 Modified Sonine approximation for the Navier–Stokes transport coefficients of a granular gas. Physica A 376, 94–107.CrossRefGoogle Scholar
Gayen, B. & Alam, M. 2006 Algebraic and exponential instabilities in a sheared micropolar granular fluid. J. Fluid Mech. 567, 195–231.Google Scholar
Gayen, B. & Alam, M. 2008 Orientational correlation and velocity distributions in uniform shear flow of a dilute granular gas. Phys. Rev. Lett. 100, 068002.Google Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.Google Scholar
Goldreich, P. & Tremaine, S. 1978 The velocity dispersion in Saturn’s rings. Icarus 34, 227–239.Google Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2, 331–407.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985b Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985a Kinetic theory of plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28, 3485–3494.Google Scholar
Jenkins, J. T. & Richman, M. W. 1988 Plane simple shear of smooth inelastic circular disks. J. Fluid Mech. 192, 313–328.Google Scholar
Kogan, M. N. 1969 Rarefied Gas Dynamics. Plenum Press.Google Scholar
Kremer, G. M. & Marques, W. 2011 Fourteen moment theory for granular gases. Kinet. Relat. Models 4, 317–331.CrossRefGoogle Scholar
Latter, H. N. & Ogilvie, G. I. 2006 The linear stability of dilute particulate rings. Icarus 184, 498–516.Google Scholar
Lees, A. W. & Edwards, S. 1972 The computer study of transport processes under extreme conditions. J. Phys. C 5, 1921–1929.CrossRefGoogle Scholar
Lutsko, J. F. 2004 Rheology of dense polydisperse granular fluids under shear. Phys. Rev. E 70, 061101.Google Scholar
Lutsko, J. F. 2005 Transport properties of dense dissipative hard-sphere fluids for arbitrary energy loss models. Phys. Rev. E 72, 021306.Google Scholar
Mitarai, N. & Nakanishi, H. 2007 Velocity correlations in dense granular shear flows: effects on energy dissipation and normal stress. Phys. Rev. E 75, 031305.Google Scholar
Mitarai, N., Nakanishi, H. & Hayakawa, H. 2002 Collisional granular flow as a micropolar fluid. Phys. Rev. Lett. 88, 174301.Google Scholar
Montanero, J. M., Garzo, V., Alam, M. & Luding, S. 2006 Rheology of two- and three-dimensional granular mixtures under uniform shear flow: Enskog kinetic theory versus molecular dynamics simulations. Granul. Matt. 8, 103–115.Google Scholar
Rao, K. K. R. & Nott, P. R. 2008 An Introduction to Granular Flow. Cambridge University Press.Google Scholar
Rongali, R. & Alam, M. 2014 Higher-order effects on orientational correlation and relaxation dynamics in homogeneous cooling of a rough granular gas. Phys. Rev. E 89, 062201.Google Scholar
Rosenau, P. 1989 Extending hydrodynamics via the regularization of the Chapman–Enskog expansion. Phys. Rev. A 40, 7193–7196.CrossRefGoogle ScholarPubMed
Saha, S. & Alam, M.2014 Conductivity and Dufour tensors in a sheared granular gas (in preparation).Google Scholar
Santos, A. 2008 Does the Chapman–Enskog expansion for sheared granular gases converge? Phys. Rev. Lett. 100, 078003.CrossRefGoogle ScholarPubMed
Santos, A., Garzo, V. & Dufty, J. W. 2004 Inherent rheology of a granular fluid in uniform shear. Phys. Rev. E 69, 061303.Google Scholar
Savage, S. B. & Jeffrey, D. J. 1981 The stress tensor in a granular flow at high shear rates. J. Fluid Mech. 110, 255–272.Google Scholar
Schmidt, J., Salo, H., Spahn, F. & Petzschmann, O. 2001 Viscous overstability in Saturn’s B-ring: hydrodynamic theory and comparison to simulations. Icarus 153, 316–331.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres. J. Fluid Mech. 361, 41–74.Google Scholar
Sela, N., Goldhirsch, I. & Noskowicz, S. H. 1996 Kinetic theoretical study of a simply sheared two-dimensional granular gas to Burnett order. Phys. Fluids 8, 2337–2353.CrossRefGoogle Scholar
Shukhman, G. 1984 Collisional dynamics of particles in Saturn’s rings. Sov. Astron. 28, 547–584.Google Scholar
Shukla, P. & Alam, M. 2009 Order parameter description of shear-banding in granular Couette flow via Landau equation. Phys. Rev. Lett. 103, 068001.Google Scholar
Shukla, P. & Alam, M. 2011a Nonlinear stability and patterns in granular plane Couette flow: Hopf and pitchfork bifurcations, and evidence for resonance. J. Fluid Mech. 672, 147–195.Google Scholar
Shukla, P. & Alam, M. 2011b Weakly nonlinear theory of shear-banding instability in granular plane Couette flow: analytical solution, comparison with numerics and bifurcation. J. Fluid Mech. 666, 204–253.Google Scholar
Simon, V. & Jenkins, J. T. 1994 On the vertical structure of dilute planetary rings. Icarus 110, 109–116.Google Scholar
Torrilhon, M. & Struchtrup, H. 2004 Regularized 13-moment equations: shock structure calculations and comparison to Burnett models. J. Fluid Mech. 513, 171–198.Google Scholar
Truesdell, C. & Muncaster, R. G. 1980 Fundamentals of Maxwell’s Kinetic Theory of a Simple Monatomic Gas. Academic Press.Google Scholar
Vega Reyes, F., Santos, A. & Garzo, V. 2013 Steady base states for non-Newtonian granular hydrodynamics. J. Fluid Mech. 719, 431–464.Google Scholar
Verlet, L. & Levesque, D. 1982 Integral equations for classical fluids III. The hard disk system. Mol. Phys. 46, 969–980.Google Scholar