Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T01:55:57.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-unique bubble dynamics in a vertical capillary with an external flow

Published online by Cambridge University Press:  01 February 2021

Yingxian Estella Yu Open the ORCID record for Yingxian Estella Yu [Opens in a new window] ,
Mirco Magnini Open the ORCID record for Mirco Magnini [Opens in a new window] ,
Lailai Zhu Open the ORCID record for Lailai Zhu [Opens in a new window] ,
Suin Shim Open the ORCID record for Suin Shim [Opens in a new window]  and
Howard A. Stone Open the ORCID record for Howard A. Stone [Opens in a new window]
Yingxian Estella Yu
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ08544, USA
Mirco Magnini
Affiliation:
Department of Mechanical, Materials and Manufacturing Engineering, University of Nottingham, NottinghamNG7 2RD, UK
Lailai Zhu
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ08544, USA Department of Mechanical Engineering, National University of Singapore, 117575, Republic of Singapore
Suin Shim
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ08544, USA
Howard A. Stone*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ08544, USA
*
†Email address for correspondence: hastone@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

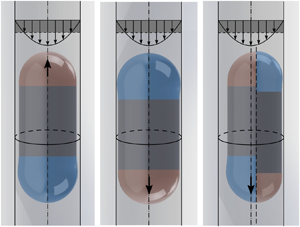
We study bubble motion in a vertical capillary tube under an external flow. Bretherton (J. Fluid Mech., vol. 10, issue 2, 1961, pp. 166–188) has shown that, without external flow, a bubble can spontaneously rise when the Bond number (${Bo} \equiv \rho g R^2 / \gamma$) is above the critical value ${Bo}_{cr}=0.842$, where $\rho$ is the liquid density, $g$ the gravitational acceleration, $R$ the tube radius and $\gamma$ the surface tension. It was then shown by Magnini et al. (Phys. Rev. Fluids, vol. 4, issue 2, 2019, 023601) that the presence of an imposed liquid flow, in the same (upward) direction as buoyancy, accelerates the bubble and thickens the liquid film around it. In this work we carry out a systematic study of the bubble motion under a wide range of upward and downward external flows, focusing on the inertialess regime with Bond numbers above the critical value. We show that a rich variety of bubble dynamics occurs when an external downward flow is applied, opposing the buoyancy-driven rise of the bubble. We reveal the existence of a critical capillary number of the external downward flow (${Ca}_l \equiv \mu U_l/\gamma$, where $\mu$ is the fluid viscosity and $U_l$ is the mean liquid speed) at which the bubble arrests and changes its translational direction. Depending on the relative direction of gravity and the external flow, the thickness of the film separating the bubble surface and the tube inner wall follows two distinct solution branches. The results from theory, experiments and numerical simulations confirm the existence of the two solution branches and reveal that the two branches overlap over a finite range of ${Ca}_l$, thus suggesting non-unique, history-dependent solutions for the steady-state film thickness under the same external flow conditions. Furthermore, inertialess symmetry-breaking shape profiles at steady state are found as the bubble transits near the tipping points of the solution branches, which are shown in both experiments and three-dimensional numerical simulations.

JFM classification

Drops and Bubbles: Bubble dynamics Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A34
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Araújo, J.D.P., Miranda, J.M., Pinto, A.M.F.R. & Campos, J.B.L.M. 2012 Wide-ranging survey on the laminar flow of individual Taylor bubbles rising through stagnant newtonian liquids. Intl J. Multiphase Flow 43, 131–148.10.1016/j.ijmultiphaseflow.2012.03.007CrossRefGoogle Scholar
Asayesh, F., Zarabadi, M.P. & Greener, J. 2017 A new look at bubbles during biofilm inoculation reveals pronounced effects on growth and patterning. Biomicrofluidics 11 (6), 064109.10.1063/1.5005932CrossRefGoogle Scholar
Aussillous, P. & Quéré, D. 2000 Quick deposition of a fluid on the wall of a tube. Phys. Fluids 12 (10), 2367–2371.10.1063/1.1289396CrossRefGoogle Scholar
Blunt, M.J. 2001 Flow in porous media – pore-network models and multiphase flow. Curr. Opin. Colloid Interface Sci. 6 (3), 197–207.10.1016/S1359-0294(01)00084-XCrossRefGoogle Scholar
Brackbill, J.U., Kothe, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354.10.1016/0021-9991(92)90240-YCrossRefGoogle Scholar
Bretherton, F.P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (2), 166–188.10.1017/S0022112061000160CrossRefGoogle Scholar
Collins, R., De Moraes, F.F., Davidson, J.F. & Harrison, D. 1978 The motion of a large gas bubble rising through liquid flowing in a tube. J. Fluid Mech. 89 (3), 497–514.10.1017/S0022112078002700CrossRefGoogle Scholar
Dhaouadi, W. & Kolinski, J.M. 2019 Bretherton's buoyant bubble. Phys. Rev. Fluids 4 (12), 123601.10.1103/PhysRevFluids.4.123601CrossRefGoogle Scholar
Fabre, J. & Figueroa-Espinoza, B. 2014 Taylor bubble rising in a vertical pipe against laminar or turbulent downward flow: symmetric to asymmetric shape transition. J. Fluid Mech. 755, 485–502.10.1017/jfm.2014.429CrossRefGoogle Scholar
Feinstein, S.B., Ten Cate, F.J., Zwehl, W., Ong, K., Maurer, G., Tei, C., Shah, P.M., Meerbaum, S. & Corday, E. 1984 Two-dimensional contrast echocardiography. I. In vitro development and quantitative analysis of echo contrast agents. J. Am. Coll. Cardiol. 3 (1), 14–20.10.1016/S0735-1097(84)80424-6CrossRefGoogle ScholarPubMed
Ferrari, A., Magnini, M. & Thome, J.R. 2018 Numerical analysis of slug flow boiling in square microchannels. Intl J. Heat Mass Tranfer 123, 928–944.10.1016/j.ijheatmasstransfer.2018.03.012CrossRefGoogle Scholar
Fershtman, A., Babin, V., Barnea, D. & Shemer, L 2017 On shapes and motion of an elongated bubble in downward liquid pipe flow. Phys. Fluids 29 (11), 112103.10.1063/1.4996444CrossRefGoogle Scholar
Griffith, P. & Wallis, G.B. 1961 Two-phase slug flow. J. Heat Transfer 83 (3), 307–318.10.1115/1.3682268CrossRefGoogle Scholar
Hirt, C.W. & Nichols, B.D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.10.1016/0021-9991(81)90145-5CrossRefGoogle Scholar
Hu, Y., Bian, S., Grotberg, J., Filoche, M., White, J., Takayama, S. & Grotberg, J.B. 2015 A microfluidic model to study fluid dynamics of mucus plug rupture in small lung airways. Biomicrofluidics 9 (4), 044119.10.1063/1.4928766CrossRefGoogle ScholarPubMed
Khodaparast, S., Kim, M.K., Silpe, J.E. & Stone, H.A. 2017 Bubble-driven detachment of bacteria from confined microgeometries. Environ. Sci. Technol. 51 (3), 1340–1347.10.1021/acs.est.6b04369CrossRefGoogle ScholarPubMed
Kotula, A.P. & Anna, S.L. 2012 Probing timescales for colloidal particle adsorption using slug bubbles in rectangular microchannels. Soft Matt. 8 (41), 10759–10772.10.1039/c2sm25970bCrossRefGoogle Scholar
Lamstaes, C. & Eggers, J. 2017 Arrested bubble rise in a narrow tube. J. Stat. Phys. 167 (3–4), 656–682.10.1007/s10955-016-1559-zCrossRefGoogle Scholar
Li, Z., Wang, L., Li, J. & Chen, H. 2019 Drainage of lubrication film around stuck bubbles in vertical capillaries. Appl. Phys. Lett. 115 (11), 111601.10.1063/1.5112055CrossRefGoogle Scholar
Lu, X. & Prosperetti, A. 2006 Axial stability of Taylor bubbles. J. Fluid Mech. 568, 173–192.10.1017/S0022112006002205CrossRefGoogle Scholar
Magnini, M., Ferrari, A., Thome, J.R & Stone, H.A. 2017 Undulations on the surface of elongated bubbles in confined gas–liquid flows. Phys. Rev. Fluids 2 (8), 084001.10.1103/PhysRevFluids.2.084001CrossRefGoogle Scholar
Magnini, M., Khodaparast, S., Matar, O.K., Stone, H.A. & Thome, J.R. 2019 Dynamics of long gas bubbles rising in a vertical tube in a cocurrent liquid flow. Phys. Rev. Fluids 4 (2), 023601.10.1103/PhysRevFluids.4.023601CrossRefGoogle Scholar
Magnini, M. & Matar, O.K. 2020 Numerical study of the impact of the channel shape on microchannel boiling heat transfer. Intl J. Heat Mass Tranfer 150, 119322.10.1016/j.ijheatmasstransfer.2020.119322CrossRefGoogle Scholar
Martin, C.S. 1976 Vertically downward two-phase slug flow. Trans. ASME: J. Fluids Engng 98 (4), 715–722.Google Scholar
Nicklin, D.J. 1962 Two-phase flow in vertical tubes. Inst. Chem. Engr. 40 (1), 61–68.Google Scholar
Polonsky, S., Barnea, D. & Shemer, L. 1999 Averaged and time-dependent characteristics of the motion of an elongated bubble in a vertical pipe. Intl J. Multiphase Flow 25 (5), 795–812.10.1016/S0301-9322(98)00066-4CrossRefGoogle Scholar
Quéré, D. 1999 Fluid coating on a fiber. Annu. Rev. Fluid Mech. 31 (1), 347–384.10.1146/annurev.fluid.31.1.347CrossRefGoogle Scholar
Taitel, Y., Barnea, D. & Dukler, A.E. 1980 Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 26 (3), 345–354.10.1002/aic.690260304CrossRefGoogle Scholar
Thulasidas, T.C., Abraham, M.A. & Cerro, R.L. 1995 Bubble-train flow in capillaries of circular and square cross section. Chem. Engng Sci. 50 (2), 183–199.10.1016/0009-2509(94)00225-GCrossRefGoogle Scholar
Uhlendorf, V. & Hoffmann, C. 1994 Nonlinear acoustical response of coated microbubbles in diagnostic ultrasound. In Proceedings of IEEE Ultrasonics Symposium, vol. 3, pp. 1559–1562. IEEE.10.1109/ULTSYM.1994.401889CrossRefGoogle Scholar
Yu, Y.E., Khodaparast, S. & Stone, H.A. 2017 Armoring confined bubbles in the flow of colloidal suspensions. Soft Matt. 13 (15), 2857–2865.10.1039/C6SM02585DCrossRefGoogle ScholarPubMed
Yu, Y.E., Zhu, L., Shim, S., Eggers, J. & Stone, H.A. 2018 Time-dependent motion of a confined bubble in a tube: transition between two steady states. J. Fluid Mech. 857, R4.10.1017/jfm.2018.835CrossRefGoogle Scholar
Zhou, G. & Prosperetti, A. 2019 Violent expansion of a rising Taylor bubble. Phys. Rev. Fluids 4 (7), 073903.10.1103/PhysRevFluids.4.073903CrossRefGoogle Scholar
Supplementary material: File

Yu et al. supplementary material

Yu et al. supplementary material

Download Yu et al. supplementary material(File)
File 1.7 MB