Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T20:32:04.295Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical analysis of bluff body wakes under periodic open-loop control

Published online by Cambridge University Press:  17 December 2013

Derwin J. Parkin Open the ORCID record for Derwin J. Parkin [Opens in a new window] ,
M. C. Thompson  and
J. Sheridan
Derwin J. Parkin*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
J. Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
*
†Email address for correspondence: dparkin7@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Large eddy simulations at 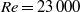$Re= 23\hspace{0.167em} 000$ are used to investigate the drag on a two-dimensional elongated cylinder caused by rear-edge periodic actuation, with particular focus on an optimum open-loop configuration. The 3.64 (length/thickness) aspect-ratio cylinder has a rectangular cross-section with rounded leading corners, representing the two-dimensional cross-section of the now generic Ahmed-body geometry. The simulations show that the optimum drag reduction occurs in the forcing Strouhal number range of 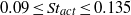$0. 09\leq S{t}_{act} \leq 0. 135$, which is approximately half of the Strouhal number corresponding to shedding of von Kármán vortices into the wake for the natural case. This result agrees well with recent experiments of Henning et al. (Active Flow Control, vol. 95, 2007, pp. 369–390). A thorough transient wake analysis employing dynamic mode decomposition is conducted for all cases, with special attention paid to the Koopman modes of the wake flow and vortex progression downstream. Two modes are found to coexist in all cases, the superimposition of which recovers the majority of features observed in the flow. Symmetric vortex shedding in the near wake, which effectively extends the mean recirculation bubble, is shown to be the major mechanism in lowering the drag. This is associated with opposite-signed vortices reducing the influence of natural vortex shedding, resulting in an increase in the pressure in the near wake, while the characteristic wake antisymmetry returns further downstream. Lower-frequency actuation is shown to create larger near-wake symmetric vortices, which improves the effectiveness of this process.

JFM classification

Flow Control: Drag reduction Flow Control: Instability control Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 94 - 123
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, S. & Ramm, G. 1984 Some salient features of the time averaged ground vehicle wake. SAE Paper no. 840300.CrossRefGoogle Scholar
Bearman, P. W. 1967 The effect of base bleed on the flow behind a two-dimensional model with a blunt trailing edge. Aeronaut. Q. 18, 207–224.Google Scholar
Chiekh, M. B., Michard, M., Guellouz, M. S. & Bera, J. C. 2013 POD analysis of momentumless trailing edge wake using synthetic jet actuation. Exp. Therm. Fluid Sci. 46, 89–102.Google Scholar
Cooper, K. R. 1985 The effect of front-edge rounding and rear-edge shaping on the aerodynamic drag of bluff vehicles in ground proximity. SAE Technical Paper 850288.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy-viscosity model. Phys. Fluids 3 (7), 1760–1765.Google Scholar
Glezer, A. 2011 Some aspects of aerodynamic flow control using synthetic-jet actuation. Phil. Trans. R. Soc. A 369, 1476–1494.Google Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12, 1422–1429.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013 Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.Google Scholar
Hackett, J. E., Wilsden, D. J. & Lilley, E. E. 1979 Estimation of tunnel blockage from wall pressure signatures: a review and data correlation. NASA CR 152, 241.Google Scholar
Henning, L., Pastoor, M., King, R., Noack, B. R. & Tadmor, G. 2007 Feedback control applied to the bluff body wake. Active Flow Control 95, 369–390.Google Scholar
Hourigan, K., Thompson, M. C. & Tan, B. T. 2001 Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 15, 387–398.Google Scholar
Hsu, T. Y., Hammache, M. & Browand, F. 2002 Base flaps and oscillatory perturbations to decrease base drag. In The Aerodynamics of Heavy Vehicles: Trucks, Buses, and Trains, vol. 1, pp. 303–316. Springer.Google Scholar
Huerre, P. & Monkewitz, P. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Krajnovic, S. 2009 Large eddy simulation of flows around ground vehicles and other bluff bodies. Phil. Trans. R Soc. A 367, 2917–2930.CrossRefGoogle ScholarPubMed
Krajnovic, S. & Fernandes, J. 2011 Numerical simulation of the flow around a simplified vehicle model with active flow control. Intl J. Heat and Fluid Flow 32, 192–200.CrossRefGoogle Scholar
Lehmkuhl, O., Rodríguez, I., Borrell, R., Pérez-Segarra, C. D. & Oliva, A. 2011 Low-frequency variations in the wake of a circular cylinder at $Re= 3900$ . J. Phys.: Conf. Ser. 318, 042038.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4 (3), 633–635.CrossRefGoogle Scholar
Mercker, E. 1986 A blockage correction for automotive testing in a wind tunnel with closed test section. J. Wind Engng & Indust. Aerodyn 22, 149–167.CrossRefGoogle Scholar
Mezic, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.Google Scholar
Mills, R., Sheridan, J. & Hourigan, K. 2001 Response of base suction and vortex shedding from rectangular prisms to transverse forcing. J. Fluid Mech. 461, 25–49.Google Scholar
Nishri, B. & Wygnanski, I. 1998 Effects of periodic excitation on turbulent flow separation from a flap. AIAA J. 36 (4), 547–556.Google Scholar
Park, H., Lee, D., Jeon, W., Hahn, S. & Kim, J. 2006 Drag reduction in flow over a two-dimensional bluff body with a blunt trailing edge using a new passive device. J. Fluid Mech. 563, 389–414.CrossRefGoogle Scholar
Pastoor, M., Henning, L., Noack, B. R., King, R. & Tadmor, G. 2008 Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 608, 161–196.Google Scholar
Petrusma, M. S. & Gai, S. L. 1994 The effect of geometry on the base pressure recovery of the segmented blunt trailing edge. Aeronaut. J. 98, 267–274.Google Scholar
Rockwell, D. & Naudascher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11, 67–94.CrossRefGoogle Scholar
Rodriguez, O. 1991 Base drag reduction by the control of three-dimensional unsteady vortical structures. Exp. Fluids 11, 218–226.CrossRefGoogle Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schmid, P. J. 2011 Application of the dynamic mode decomposition to experimental data. Exp. Fluids 50, 1123–1130.Google Scholar
Scotti, A., Meneveau, C. & Fatica, M. 1997 Dynamic Smagorinsky model on anisotropic grids. Phys. Fluids 9 (6), 1856–1858.Google Scholar
Tanner, M. 1972 A method of reducing the base drag of wings with blunt trailing edges. Aeronaut. J. 23, 15–23.Google Scholar
Tombazis, N. & Bearman, P. W. 1997 A study of three-dimensional aspects of vortex shedding from a bluff body with a mild geometric disturbance. J. Fluid Mech. 330, 85–112.Google Scholar