Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:27:32.436Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of near-wake characteristics of cavitating flow over a circular cylinder

Published online by Cambridge University Press:  04 February 2016

Aswin Gnanaskandan  and
Krishnan Mahesh
Aswin Gnanaskandan
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

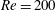A homogeneous mixture model is used to study cavitation over a circular cylinder at two different Reynolds numbers ($Re=200$ and 3900) and four different cavitation numbers (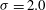${\it\sigma}=2.0$, 1.0, 0.7 and 0.5). It is observed that the simulated cases fall into two different cavitation regimes: cyclic and transitional. Cavitation is seen to significantly influence the evolution of pressure, boundary layer and loads on the cylinder surface. The cavitated shear layer rolls up into vortices, which are then shed from the cylinder, similar to a single-phase flow. However, the Strouhal number corresponding to vortex shedding decreases as the flow cavitates, and vorticity dilatation is found to play an important role in this reduction. At lower cavitation numbers, the entire vapour cavity detaches from the cylinder, leaving the wake cavitation-free for a small period of time. This low-frequency cavity detachment is found to occur due to a propagating condensation front and is discussed in detail. The effect of initial void fraction is assessed. The speed of sound in the free stream is altered as a result and the associated changes in the wake characteristics are discussed in detail. Finally, a large-eddy simulation of cavitating flow at 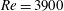$Re=3900$ and 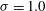${\it\sigma}=1.0$ is studied and a higher mean cavity length is obtained when compared to the cavitating flow at 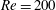$Re=200$ and 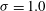${\it\sigma}=1.0$. The wake characteristics are compared to the single-phase results at the same Reynolds number and it is observed that cavitation suppresses turbulence in the near wake and delays three-dimensional breakdown of the vortices.

JFM classification

Drops and Bubbles: Cavitation Vortex Flows: Vortex dynamics Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , pp. 453 - 491
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakeri, V. H. 1975 Viscous effects on the position of cavitation separation from smooth bodies. J. Fluid Mech. 68 (4), 779–799.CrossRefGoogle Scholar
Arakeri, V. H. & Acosta, A. J. 1973 Viscous effects in the inception of cavitation on axisymmetric bodies. Trans. ASME J. Fluids Engng 95 (4), 519–527.CrossRefGoogle Scholar
Arndt, R. E. A. 2002 Cavitation in vortical flows. Annu. Rev. Fluid Mech. 34 (1), 143–175.CrossRefGoogle Scholar
Arndt, R. E. A. & Maines, B. H. 2000 Nucleation and bubble dynamics in vortical flows. Trans. ASME J. Fluids Engng 122 (3), 488–493.CrossRefGoogle Scholar
Arndt, R. E. A., Song, C. C. S., Kjeldsen, M., He, J. & Keller, A. 2000 Instability of partial cavitation: a numerical/experimental approach. In Proceedings of the 23rd Symposium on Naval Hydrodynamics, pp. 519–615. National Academies Press.Google Scholar
Balachandar, R. & Ramamurthy, A. S. 1999 Pressure distribution in cavitating circular cylinder wakes. J. Engng Mech. 125 (3), 356–358.Google Scholar
Bearman, P. W. 1969 On vortex shedding from a circular cylinder in the critical Reynolds number regime. J. Fluid Mech. 37 (3), 577–585.CrossRefGoogle Scholar
Belahadji, B., Franc, J.-P. & Michel, J.-M. 1995 Cavitation in the rotational structures of a turbulent wake. J. Fluid Mech. 287, 383–403.CrossRefGoogle Scholar
Brandner, P. A., Walker, G. J., Niekamp, P. N. & Anderson, B. 2010 An experimental investigation of cloud cavitation about a sphere. J. Fluid Mech. 656, 147–176.CrossRefGoogle Scholar
Colonius, T. 2004 Modeling artificial boundary conditions for compressible flow. Annu. Rev. Fluid Mech. 36, 315–345.CrossRefGoogle Scholar
Coutier-Delgosha, O., Stutz, B., Vabre, A. & Legoupil, S. 2007 Analysis of cavitating flow structure by experimental and numerical investigations. J. Fluid Mech. 578, 171–222.CrossRefGoogle Scholar
Dipankar, A., Sengupta, T. K. & Talla, S. B. 2007 Suppression of vortex shedding behind a circular cylinder by another control cylinder at low Reynolds numbers. J. Fluid Mech. 573, 171–190.CrossRefGoogle Scholar
Franc, J.-P. & Michel, J.-M. 1985 Attached cavitation and the boundary layer: experimental investigation and numerical treatment. J. Fluid Mech. 154, 63–90.CrossRefGoogle Scholar
Franc, J.-P. & Michel, J.-M. 1988 Unsteady attached cavitation on an oscillating hydrofoil. J. Fluid Mech. 193, 171–189.CrossRefGoogle Scholar
Fry, S. 1984 Investigating cavity/wake dynamics for a circular cylinder by measuring noise spectra. J. Fluid Mech. 142, 187–200.CrossRefGoogle Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25 (2), 401–413.CrossRefGoogle Scholar
Gnanaskandan, A. & Mahesh, K. 2014 Large eddy simulation of sheet to cloud cavitation. In Proceedings of the 30th Symposium on Naval Hydrodynamics, pp. 1–13.Google Scholar
Gnanaskandan, A. & Mahesh, K. 2015 A numerical method to simulate turbulent cavitating flows. Intl J. Multiphase Flow 70, 22–34.CrossRefGoogle Scholar
Hammache, M. & Gharib, M. 1991 An experimental study of the parallel and oblique vortex shedding from circular cylinders. J. Fluid Mech. 232, 567–590.CrossRefGoogle Scholar
Hsiao, C.-T. & Chahine, G. L. 2005 Scaling of tip vortex cavitation inception noise with a bubble dynamics model accounting for nuclei size distribution. Trans. ASME J. Fluids Engng 127 (1), 55–65.CrossRefGoogle Scholar
Katz, J.1982 Cavitation inception in seperated flows. PhD thesis, California Institute of Technology.Google Scholar
Katz, J. 1984 Cavitation phenomena within regions of flow separation. J. Fluid Mech. 140, 397–436.CrossRefGoogle Scholar
Kubota, A., Kato, H. & Yamaguchi, H. 1992 A new modelling of cavitating flows: a numerical study of unsteady cavitation on a hydrofoil section. J. Fluid Mech. 240, 59–96.CrossRefGoogle Scholar
Kunz, R. F., Boger, D. A., Stinebring, D. R., Chyczewski, T. S., Lindau, J. W., Gibeling, H. J., Venkateswaran, S. & Govindan, T. R. 2000 A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 29 (8), 849–875.CrossRefGoogle Scholar
Laberteaux, K. R. & Ceccio, S. L. 2001 Partial cavity flows. Part 1. Cavities forming on models without spanwise variation. J. Fluid Mech. 431, 1–41.CrossRefGoogle Scholar
Matsudaira, Y., Gomi, Y. & Oba, R. 1992 Characteristics of bubble-collapse pressures in a Karman-vortex cavity. JSME Intl J. 35 (2), 179–185.Google Scholar
Mittal, S. & Raghuvanshi, A. 2001 Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Intl J. Numer. Meth. Fluids 35 (4), 421–447.3.0.CO;2-M>CrossRefGoogle Scholar
Park, N. & Mahesh, K. 2007 Numerical and modeling issues in LES of compressible turbulence on unstructured grids. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, AIAA Paper, pp. 1–18.Google Scholar
Ramamurthy, A. S. & Bhaskaran, P. 1977 Constrained flow past cavitating bluff bodies. Trans. ASME J. Fluids Engng 99 (4), 717–726.CrossRefGoogle Scholar
Rao, B. C. S. & Chandrasekhara, D. V. 1976 Some characteristics of cavity flow past cylindrical inducers in a venturi. Trans. ASME J. Fluids Engng 98 (3), 461–466.Google Scholar
Rao, B. C. S., Chandrasekhara, D. V. & Seetharamiah, K. 1972 A high-speed photographic study of vortex shedding behind circular cylinders of cavitating flows. In Proceedings of 2nd International JSME Symposium Fluid Machinery and Fluidics, pp. 293–302.Google Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (3), 345–356.CrossRefGoogle Scholar
Rouse, H. & McNown, J. S.1948 Cavitation and pressure distribution: head forms at zero angle of yaw. State University of Iowa, Studies in Engineering, Bulletin 32. Published by the State University of Iowa.Google Scholar
Saito, Y. & Sato, K. 2003 Cavitation bubble collapse and impact in the wake of a circular cylinder. In Proceedings of the 5th International Symposium on Cavitation, pp. 1–6.Google Scholar
Saito, Y., Takami, R., Nakamori, I. & Ikohagi, T. 2007 Numerical analysis of unsteady behavior of cloud cavitation around a NACA0015 foil. Comput. Mech. 40 (1), 85–96.CrossRefGoogle Scholar
Schmidt, S. J., Schnerr, G. & Thalhamer, M. 2009 Inertia controlled instability and small scale structures of sheet and cloud cavitation. In Proceedings of the 7th International Symposium on Cavitation, pp. 1–14.Google Scholar
Schnerr, G. H., Sezal, I. H. & Schmidt, S. J. 2008 Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock dynamics. Phys. Fluids 20 (4), 1–9.CrossRefGoogle Scholar
Selim, S. M.1981 Cavitation erosion in fluid flow. PhD thesis, University of Southampton.Google Scholar
Senocak, I. & Shyy, W. 2002 A pressure-based method for turbulent cavitating flow computations. J. Comput. Phys. 176 (2), 363–383.CrossRefGoogle Scholar
Seo, J. H., Moon, Y. J. & Shin, B. R. 2008 Prediction of cavitating flow noise by direct numerical simulation. J. Comput. Phys. 227 (13), 6511–6531.CrossRefGoogle Scholar
Shin, B. R., Iwata, Y. & Ikohagi, T. 2003 Numerical simulation of unsteady cavitating flows using a homogenous equilibrium model. Comput. Mech. 30 (5–6), 388–395.CrossRefGoogle Scholar
Singhal, A. K., Athavale, M. M., Li, H. & Jiang, Y. 2002 Mathematical basis and validation of the full cavitation model. Trans. ASME J. Fluids Engng 124 (3), 617–624.CrossRefGoogle Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex shedding at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
Varga, J. J. & Sebestyen, G. Y. 1972 Determination of hydrodynamic cavitation intensity by noise measurement. In Proceedings of the 2nd International JSME Symposium on Fluid Machinery and Fluidics, pp. 285–292.Google Scholar
Verma, A. & Mahesh, K. 2012 A Lagrangian subgrid-scale model with dynamic estimation of Lagrangian time scale for large eddy simulation of complex flows. Phys. Fluids 24 (8), 85–101.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.CrossRefGoogle Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.CrossRefGoogle Scholar
Yee, H. C., Sandham, N. D. & Djomehri, M. J. 1999 Low-dissipative high-order shock-capturing methods using characteristic-based filters. J. Comput. Phys. 150 (1), 199–238.CrossRefGoogle Scholar
Young, J. O. & Holl, J. W. 1966 Effects of cavitation on periodic wakes behind symmetric wedges. Trans. ASME J. Fluids Engng 88 (1), 163–176.CrossRefGoogle Scholar