Hostname: page-component-6bb9c88b65-dwch4 Total loading time: 0 Render date: 2025-07-24T01:32:19.325Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of shear-flow free-surface turbulence and air entrainment at large Froude and Weber numbers

Published online by Cambridge University Press:  07 October 2019

Xiangming Yu ,
Kelli Hendrickson Open the ORCID record for Kelli Hendrickson [Opens in a new window] ,
Bryce K. Campbell  and
Dick K. P. Yue Open the ORCID record for Dick K. P. Yue [Opens in a new window]
Xiangming Yu
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Kelli Hendrickson
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Bryce K. Campbell
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: yue@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

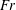We investigate two-phase free-surface turbulence (FST) associated with an underlying shear flow under the condition of strong turbulence (SFST) characterized by large Froude ($Fr$) and Weber (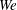$We$) numbers. We perform direct numerical simulations of three-dimensional viscous flows with air and water phases. In contrast to weak FST (WFST) with small free-surface distortions and anisotropic underlying turbulence with distinct inner/outer surface layers, we find SFST to be characterized by large surface deformation and breaking accompanied by substantial air entrainment. The interface inner/outer surface layers disappear under SFST, resulting in nearly isotropic turbulence with 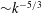${\sim}k^{-5/3}$ scaling of turbulence kinetic energy near the interface (where 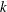$k$ is wavenumber). The SFST air entrainment is observed to occur over a range of scales following a power law of slope 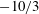$-10/3$. We derive this using a simple energy argument. The bubble size spectrum in the volume follows this power law (and slope) initially, but deviates from this in time due to a combination of ongoing broad-scale entrainment and bubble fragmentation by turbulence. For varying 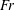$Fr$ and 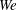$We$, we find that air entrainment is suppressed below critical values 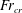$Fr_{cr}$ and 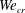$We_{cr}$. When 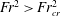$Fr^{2}>Fr_{cr}^{2}$ and 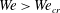$We>We_{cr}$, the entrainment rate scales as 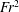$Fr^{2}$ when gravity dominates surface tension in the bubble formation process, while the entrainment rate scales linearly with 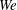$We$ when surface tension dominates.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 209 - 238
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

André, M. A. & Bardet, P. M. 2017 Free surface over a horizontal shear layer: vorticity generation and air entrainment mechanisms. J. Fluid Mech. 813, 1007–1044.Google Scholar
Borue, V., Orszag, S. A. & Staroselsky, I. 1995 Interaction of surface waves with turbulence: direct numerical simulations of turbulent open-channel flow. J. Fluid Mech. 286, 1–23.Google Scholar
Brackbill, J. U., Kothe, D. B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100 (2), 335–354.Google Scholar
Brocchini, M. 2002 Free surface boundary conditions at a bubbly/weakly splashing air–water interface. Phys. Fluids 14 (6), 1834–1840.Google Scholar
Brocchini, M. & Peregrine, D. H. 2001a The dynamics of strong turbulence at free surfaces. Part 1. Description. J. Fluid Mech. 449, 225–254.Google Scholar
Brocchini, M. & Peregrine, D. H. 2001b The dynamics of strong turbulence at free surfaces. Part 2. Free-surface boundary conditions. J. Fluid Mech. 449, 255–290.Google Scholar
Campbell, B. K.2015 A mechanistic investigation of nonlinear interfacial instabilities leading to slug formation in multiphase flows. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Chachereau, Y. & Chanson, H. 2011 Free-surface fluctuations and turbulence in hydraulic jumps. Exp. Therm. Fluid Sci. 35 (6), 896–909.Google Scholar
Chanson, H. & Toombes, L. 2003 Strong interactions between free-surface aeration and turbulence in an open channel flow. Exp. Therm. Fluid Sci. 27 (5), 525–535.Google Scholar
Cormen, T. H., Leiserson, C. E., Rivest, R. L. & Stein, C. 2009 Introduction to Algorithms. MIT Press.Google Scholar
Deane, G. B. & Stokes, M. D. 2002 Scale dependence of bubble creation mechanisms in breaking waves. Nature 418 (6900), 839–844.Google Scholar
Deike, L., Melville, W. K. & Popinet, S. 2016 Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 801, 91–129.Google Scholar
Falgout, R. D., Jones, J. E. & Yang, U. M. 2006 The design and implementation of hypre, a library of parallel high performance preconditioners. In Numerical Solution of Partial Differential Equations on Parallel Computers, pp. 267–294. Springer.Google Scholar
Falgout, R. D. & Yang, U. M. 2002 hypre: A library of high performance preconditioners. In Computational Science – ICCS 2002, pp. 632–641. Springer.Google Scholar
Fulgosi, M., Lakehal, D., Banerjee, S. & De Angelis, V. 2003 Direct numerical simulation of turbulence in a sheared air–water flow with a deformable interface. J. Fluid Mech. 482, 319–345.Google Scholar
Garrett, C., Li, M. & Farmer, D. 2000 The connection between bubble size spectra and energy dissipation rates in the upper ocean. J. Phys. Oceanogr. 30 (9), 2163–2171.Google Scholar
Guo, X. & Shen, L. 2010 Interaction of a deformable free surface with statistically steady homogeneous turbulence. J. Fluid Mech. 658, 33–62.Google Scholar
Handler, R. A., Swean, T. F., Leighton, R. I. & Swearingen, J. D. 1993 Length scales and the energy balance for turbulence near a free surface. AIAA J. 31 (11), 1998–2007.Google Scholar
Hong, W. L. & Walker, D. T. 2000 Reynolds-averaged equations for free-surface flows with application to high-Froude-number jet spreading. J. Fluid Mech. 417, 183–209.Google Scholar
Hunt, J. C. R., Stretch, D. D. & Belcher, S. E. 2011 Viscous coupling of shear-free turbulence across nearly flat fluid interfaces. J. Fluid Mech. 671, 96–120.Google Scholar
Liu, S., Kermani, A., Shen, L. & Yue, D. K. P. 2009 Investigation of coupled air–water turbulent boundary layers using direct numerical simulations. Phys. Fluids 21 (6), 062108.Google Scholar
Lundgren, T. S.2003 Linearly forced isotropic turbulence. Tech. Rep. Minnesota Univ. Minneapolis.Google Scholar
Mattingly, G. E. & Criminale, W. O. 1972 The stability of an incompressible two-dimensional wake. J. Fluid Mech. 51 (2), 233–272.Google Scholar
Morales, J. J., Nuevo, M. J. & Rull, L. F. 1990 Statistical error methods in computer simulations. J. Comput. Phys. 89 (2), 432–438.Google Scholar
Mortazavi, M., Le Chenadec, V., Moin, P. & Mani, A. 2016 Direct numerical simulation of a turbulent hydraulic jump: turbulence statistics and air entrainment. J. Fluid Mech. 797, 60–94.Google Scholar
Murzyn, F., Mouaze, D. & Chaplin, J. R. 2007 Air–water interface dynamic and free surface features in hydraulic jumps. J. Hydraul Res. 45 (5), 679–685.Google Scholar
Nagaosa, R. 1999 Direct numerical simulation of vortex structures and turbulent scalar transfer across a free surface in a fully developed turbulence. Phys. Fluids 11 (6), 1581–1595.Google Scholar
Pan, Y. & Banerjee, S. 1995 A numerical study of free-surface turbulence in channel flow. Phys. Fluids 7 (7), 1649–1664.Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.Google Scholar
Prosperetti, A. 1981 Motion of two superposed viscous fluids. Phys. Fluids 24 (7), 1217–1223.Google Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.Google Scholar
Savelsberg, R. & van de Water, W. 2008 Turbulence of a free surface. Phys. Rev. Lett. 100 (3), 034501.Google Scholar
Savelsberg, R. & van de Water, W. 2009 Experiments on free-surface turbulence. J. Fluid Mech. 619, 95–125.Google Scholar
Shen, L., Triantafyllou, G. S. & Yue, D. K. P. 2000 Turbulent diffusion near a free surface. J. Fluid Mech. 407, 145–166.Google Scholar
Shen, L., Triantafyllou, G. S. & Yue, D. K. P. 2001 Mixing of a passive scalar near a free surface. Phys. Fluids 13 (4), 913–926.Google Scholar
Shen, L. & Yue, D. K. P. 2001 Large-eddy simulation of free-surface turbulence. J. Fluid Mech. 440, 75–116.Google Scholar
Shen, L., Zhang, X., Yue, D. K. P. & Triantafyllou, G. S. 1999 The surface layer for free-surface turbulent flows. J. Fluid Mech. 386, 167–212.Google Scholar
Smolentsev, S. & Miraghaie, R. 2005 Study of a free surface in open-channel water flows in the regime from ‘weak’ to ‘strong’ turbulence. Intl J. Multiphase Flow 31 (8), 921–939.Google Scholar
Walker, D. T., Chen, C.-Y. & Willmarth, W. W. 1995 Turbulent structure in free-surface jet flows. J. Fluid Mech. 291, 223–261.Google Scholar
Walker, D. T., Leighton, R. I. & Garza-Rios, L. O. 1996 Shear-free turbulence near a flat free surface. J. Fluid Mech. 320, 19–51.Google Scholar
Wang, Z., Yang, J. & Stern, F. 2016 High-fidelity simulations of bubble, droplet and spray formation in breaking waves. J. Fluid Mech. 792, 307–327.Google Scholar
Weymouth, G. D. & Yue, D. K. P. 2010 Conservative volume-of-fluid method for free-surface simulations on cartesian-grids. J. Comput. Phys. 229 (8), 2853–2865.Google Scholar
Yamamoto, Y. & Kunugi, T. 2011 Direct numerical simulation of a high-Froude-number turbulent open-channel flow. Phys. Fluids 23 (12), 125108.Google Scholar
Yu, X., Hendrickson, K. & Yue, D. K. P. 2016 Air entrainment in free-surface turbulence. In Proc. 31st Symposium on Naval Hydrodynamics, Monterey, CA, USA.Google Scholar