Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T07:16:17.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical simulation of shear-induced instabilities in internal solitary waves

Published online by Cambridge University Press:  22 August 2011

Magda Carr ,
Stuart E. King  and
David G. Dritschel
Magda Carr*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, Fife KY16 9SS, UK
Stuart E. King
Affiliation:
School of Mathematics and Statistics, University of St Andrews, Fife KY16 9SS, UK
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, Fife KY16 9SS, UK
*
†Email address for correspondence: magda@mcs.st-and.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical method that employs a combination of contour advection and pseudo-spectral techniques is used to simulate shear-induced instabilities in an internal solitary wave (ISW). A three-layer configuration for the background stratification, in which a linearly stratified intermediate layer is sandwiched between two homogeneous ones, is considered throughout. The flow is assumed to satisfy the inviscid, incompressible, Oberbeck–Boussinesq equations in two dimensions. Simulations are initialized by fully nonlinear, steady-state, ISWs. The results of the simulations show that the instability takes place in the pycnocline and manifests itself as Kelvin–Helmholtz billows. The billows form near the trough of the wave, subsequently grow and disturb the tail. Both the critical Richardson number (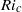) and the critical amplitude required for instability are found to be functions of the ratio of the undisturbed layer thicknesses. It is shown, therefore, that the constant, critical bound for instability in ISWs given in Barad & Fringer (J. Fluid Mech., vol. 644, 2010, pp. 61–95), namely 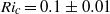, is not a sufficient condition for instability. It is also shown that the critical value of 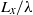required for instability, where 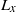is the length of the region in a wave in which 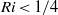and 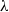is the half-width of the wave, is sensitive to the ratio of the layer thicknesses. Similarly, a linear stability analysis reveals that 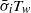(where 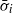is the growth rate of the instability averaged over 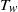, the period in which parcels of fluid are subjected to 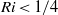) is very sensitive to the transition between the undisturbed pycnocline and the homogeneous layers, and the amplitude of the wave. Therefore, the alternative tests for instability presented in Fructus et al. (J. Fluid Mech., vol. 620, 2009, pp. 1–29) and Barad & Fringer (J. Fluid Mech., vol. 644, 2010, pp. 61–95), respectively, namely 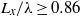and 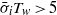, are shown to be valid only for a limited parameter range.

JFM classification

Geophysical and Geological Flows: Internal waves Waves/Free-surface Flows: Solitary waves Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 683 , 25 September 2011 , pp. 263 - 288
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Apel, J. R., Ostrovsky, L. A., Stepanyants, Y. A. & Lynch, J. F. 2006 Internal solitons in the ocean. Tech Rep. Woods Hole Oceanographic Institution.CrossRefGoogle Scholar
2. Apel, J. R., Ostrovsky, L. A., Stepanyants, Y. A. & Lynch, J. F. 2007 Internal solitons in the ocean and their effect on underwater sound. J. Acoust. Soc. Am. 121, 695–722.CrossRefGoogle ScholarPubMed
3. Armi, L. & Farmer, D. M. 1988 The flow of Mediterranean water through the Strait of Gibraltar. Prog. Oceanogr. 21, 1.Google Scholar
4. Barad, M. F. & Fringer, O. B. 2010 Simulations of shear instabilities in interfacial gravity waves. J. Fluid Mech. 644, 61–95.CrossRefGoogle Scholar
5. Benjamin, T. B. 1966 Internal waves of finite amplitude and permanent form. J. Fluid Mech. 25, 241–270.CrossRefGoogle Scholar
6. Brown, D. J. & Christie, D. R. 1998 Fully nonlinear solitary waves in continuously stratified incompressible Boussinesq fluids. Phys. Fluids 10, 2569–2586.CrossRefGoogle Scholar
7. Carr, M., Fructus, D., Grue, J., Jensen, A. & Davies, P. A. 2008 Convectively induced shear instability in large amplitude internal solitary waves. Phys. Fluids 20, 12660.Google Scholar
8. Dritschel, D. G. & Ambaum, M. H. P. 1997 A contour-advective semi-Lagrangian numerical algorithm for simulating fine-scale conservative dynamical fields. Q. J. R. Meteorol. Soc. 123, 1097–1130.Google Scholar
9. Dritschel, D. G. & Fontane, J. 2010 The combined Lagrangian advection method. J. Comput. Phys. 229, 5408–5417.CrossRefGoogle Scholar
10. Fontane, J. & Dritschel, D. G. 2009 The HyperCASL algorithm: a new approach to the numerical simulation of geophysical flows. J. Comput. Phys. 228, 6411–6425.Google Scholar
11. Fructus, D., Carr, M., Grue, J., Jensen, A. & Davies, P. A. 2009 Shear-induced breaking of large internal solitary waves. J. Fluid Mech. 620, 1–29.Google Scholar
12. Fructus, D. & Grue, J. 2004 Fully nonlinear solitary waves in a layered stratified fluid. J. Fluid Mech. 505, 323–347.Google Scholar
13. Garrett, C. 2003a Internal tides and ocean mixing. Science 301, 1858–1859.Google Scholar
14. Garrett, C. 2003b Mixing with latitude. Nature 422, 477–478.Google Scholar
15. Grue, J. 2006 Waves in Geophysical Fluids – Tsunamis, Rogue Waves, Internal Waves and Internal Tides, 1st edn. pp. 205–270. Springer.Google Scholar
16. Grue, J., Jensen, A., Rusås, P. O. & Sveen, J. K. 2000 Breaking and broadening of internal solitary waves. J. Fluid Mech. 413, 181–217.CrossRefGoogle Scholar
17. van Haren, H. & Gostiaux, L. 2010 A deep-ocean Kelvin–Helmholtz billow train. Geophys. Res. Lett. 37, L030605.CrossRefGoogle Scholar
18. Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flow. J. Fluid Mech. 51, 39–61.CrossRefGoogle Scholar
19. Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.Google Scholar
20. Helfrich, K. R. & White, B. L. 2010 A model for large-amplitude internal solitary waves with trapped cores. Nonlinear Process. Geophys. 17, 303–318.CrossRefGoogle Scholar
21. King, S. E., Carr, M. & Dritschel, D. G. 2010 The steady state form of large amplitude internal solitary waves. J. Fluid Mech. 666, 477–505.Google Scholar
22. Lamb, K. G. 2002 A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 451, 109–144.Google Scholar
23. Lamb, K. G. & Farmer, D. 2011 Instabilities in an internal solitary-like wave on the Oregon shelf. J. Phys. Oceanogr. 41, 67–87.Google Scholar
24. Long, R. R. 1965 On the Boussinesq approximation and its role in the theory of internal waves. Tellus 17, 46–52.Google Scholar
25. Marmorino, G. O. 1990 Turbulent mixing in a salt finger staircase. J. Geophy. Res. 95, 12983–12994.CrossRefGoogle Scholar
26. Miles, J. W. & Howard, L. N. 1964 Note on a heterogeneous shear flows. J. Fluid Mech. 20, 331–336.Google Scholar
27. Moum, J. N., Farmer, D. M., Smyth, W. D., Armi, L. & Vagle, S. 2003 Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. J. Phys. Oceanogr. 33, 2093–2112.Google Scholar
28. Munk, W. & Bills, B. 2007 Tides and the climate: some speculations. J. Phys. Oceanogr. 37, 135–147.Google Scholar
29. Munk, W. & Wunsch, C. 1998 Abyssal recipes. Part II. Energetics of tidal and wind mixing. Deep-Sea Res. 45, 1977–2010.CrossRefGoogle Scholar
30. Osborne, A. R. & Burch, T. L. 1980 Internal solitons in the Andaman sea. Science 208, 451–460.CrossRefGoogle ScholarPubMed
31. Osborne, A. R., Burch, T. L. & Scarlet, R. I. 1978 The influence of internal waves on deep water drilling. J. Petrol. Tech. 30, 1497–1504.CrossRefGoogle Scholar
32. Schiermeier, Q. 2007 Churn churn churn. Nature 447, 522–524.Google Scholar
33. Thorpe, S. A. 2004 Recent developments in the study of ocean turbulence. Annu. Rev. Earth Planet. Sci. 32, 91–109.Google Scholar
34. Troy, C. D. & Koseff, J. R. 2005 The instability and breaking of long internal waves. J. Fluid Mech. 543, 107–136.Google Scholar
35. Turkington, B., Eydeland, A. & Wang, S. 1991 A computational method for solitary internal waves in a continuously stratified fluid. Stud. Appl. Maths 85, 93–127.Google Scholar
36. Turner, J. S. 1980 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
37. Woods, J. D. 1968 Wave-induced shear instability in the summer thermocline. J. Fluid Mech. 32, 791–800.Google Scholar
38. Yih, C.-S. 1960 Exact solutions for steady two-dimensional flow of a stratified fluid. J. Fluid Mech. 9, 161–174.CrossRefGoogle Scholar

Carr et al. supplementary movie

Movie 1. Evolution of the vorticity field for the wave depicted in figure 2 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen

Download Carr et al. supplementary movie(Video)
Video 815.4 KB

Carr et al. supplementary movie

Movie 1. Evolution of the vorticity field for the wave depicted in figure 2 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen

Download Carr et al. supplementary movie(Video)
Video 584.4 KB

Carr et al. supplementary movie

Movie 2. Evolution of the buoyancy field for the wave depicted in figure 3 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen.

Download Carr et al. supplementary movie(Video)
Video 820.7 KB

Carr et al. supplementary movie

Movie 2. Evolution of the buoyancy field for the wave depicted in figure 3 of the manuscript. The wave is defined as stable, little or no disturbance of the pycnocline is seen.

Download Carr et al. supplementary movie(Video)
Video 574.2 KB

Carr et al. supplementary movie

Movie 3. Evolution of the vorticity field for the wave depicted in figure 4 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed.

Download Carr et al. supplementary movie(Video)
Video 839.6 KB

Carr et al. supplementary movie

Movie 3. Evolution of the vorticity field for the wave depicted in figure 4 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed.

Download Carr et al. supplementary movie(Video)
Video 610.6 KB

Carr et al. supplementary movie

Movie 4. Evolution of the buoyancy field for the wave depicted in figure 5 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed

Download Carr et al. supplementary movie(Video)
Video 846.2 KB

Carr et al. supplementary movie

Movie 4. Evolution of the buoyancy field for the wave depicted in figure 5 of the manuscript. The wave is defined as weakly unstable. Oscillation of the pycnocline is seen but no persistent coherent billows are formed

Download Carr et al. supplementary movie(Video)
Video 602.9 KB

Carr et al. supplementary movie

Movie 5. Evolution of the vorticity field for the wave depicted in figure 6 of the manuscript. The wave is defined as unstable. Coherent billows are seen in the pycnocline

Download Carr et al. supplementary movie(Video)
Video 907.9 KB

Carr et al. supplementary movie

Movie 5. Evolution of the vorticity field for the wave depicted in figure 6 of the manuscript. The wave is defined as unstable. Coherent billows are seen in the pycnocline

Download Carr et al. supplementary movie(Video)
Video 692.8 KB

Carr et al. supplementary movie

Movie 6. Evolution of the buoyancy field for the wave depicted in figure 7 of the manuscript. The wave is defined as unstable. Coherent billows are seen in the pycnocline

Download Carr et al. supplementary movie(Video)
Video 894.7 KB

Carr et al. supplementary movie

Movie 6. Evolution of the buoyancy field for the wave depicted in figure 7 of the manuscript. The wave is defined as unstable. Coherent billows are seen in the pycnocline

Download Carr et al. supplementary movie(Video)
Video 655.4 KB