Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T17:39:01.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of magnetohydrodynamic duct flow at high Reynolds and Hartmann numbers

Published online by Cambridge University Press:  03 July 2012

Dmitry Krasnov ,
Oleg Zikanov  and
Thomas Boeck
Dmitry Krasnov*
Affiliation:
Fakultät für Maschinenbau, Technische Universität Ilmenau, Postfach 100565, 98684 Ilmenau, Germany
Oleg Zikanov
Affiliation:
Department of Mechanical Engineering, University of Michigan – Dearborn, 4901 Evergreen Road, Dearborn, MI 48128-1491, USA
Thomas Boeck
Affiliation:
Fakultät für Maschinenbau, Technische Universität Ilmenau, Postfach 100565, 98684 Ilmenau, Germany
*
†Email address for correspondence: dmitry.krasnov@tu-ilmenau.de
Get access Rights & Permissions [Opens in a new window]

Abstract

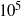High-resolution direct numerical simulations are conducted to analyse turbulent states of the flow of an electrically conducting fluid in a duct of square cross-section with electrically insulating walls and imposed transverse magnetic field. The Reynolds number of the flow is and the Hartmann number varies from 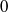to 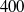. It is found that there is a broad range of Hartmann numbers in which the flow is neither laminar nor fully turbulent, but has laminar core, Hartmann boundary layers and turbulent zones near the walls parallel to the magnetic field. Analysis of turbulent fluctuations shows that each zone consists of two layers: the boundary layer near the wall characterized by small-scale turbulence and the outer layer dominated by large-scale vortical structures strongly elongated in the direction of the magnetic field. We also find a peculiar scaling of the mean velocity, according to which the reciprocal von Kármán coefficient grows nearly linearly with the distance to the wall.

JFM classification

MHD and Electrohydrodynamics: MHD turbulence Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 704 , 10 August 2012 , pp. 421 - 446
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adams, J. C., Swarztrauber, P. & Sweet, R. 1999 Efficient Fortran subprograms for the solution of separable elliptic partial differential equations. http://www.cisl.ucar.edu/css/software/fishpack/.Google Scholar
2. Baylis, J. A. 1971 Experiments on laminar flow in curved channels of square section. J. Fluid Mech. 48 (3), 417–422.CrossRefGoogle Scholar
3. Boeck, T., Krasnov, D. & Zienicke, E. 2007 Numerical study of turbulent magnetohydrodynamic channel flow. J. Fluid Mech. 572, 179.CrossRefGoogle Scholar
4. Branover, H. 1978 Magnetohydrodynamic Flow in Ducts. Wiley.Google Scholar
5. Brouillette, E. C. & Lykoudis, P. S. 1967 Magneto-fluid-mechanic channel flow. Part 1. Experiment. Phys. Fluids 10 (5), 995–1001.CrossRefGoogle Scholar
6. Burattini, P., Zikanov, O. & Knaepen, B. 2010 Decay of magnetohydrodynamic turbulence at low magnetic Reynolds number. J. Fluid Mech. 657, 502–538.CrossRefGoogle Scholar
7. Burr, U., Barleon, L., Müller, U. & Tsinober, A. 2000 Turbulent transport of momentum and heat in magnetohydrodynamic rectangular duct flow with strong sidewall jets. J. Fluid Mech. 406, 247–279.CrossRefGoogle Scholar
8. Cabral, B. & Leedom, L. 1993 Imaging vector fields using line integral convolution. In Proceedings of the SIGGRAPH ’93, Computer Graphics 27, Annual Conference Series, pp. 263–272. ACM SIGGRAPH.Google Scholar
9. Chaudhary, R., Vanka, S. P. & Thomas, B. G. 2010 Direct numerical simulations of magnetic field effects on turbulent flow in a square duct. Phys. Fluids 22 (7), 075102.CrossRefGoogle Scholar
10. Davidson, P. A. 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
11. Dey, P. & Zikanov, O. 2012 Turbulent flow and transport of passive scalar in magnetohydrodynamic channel flows with different orientations of magnetic field. Intl J. Heat Fluid Flow (in press).CrossRefGoogle Scholar
12. Favier, B., Godeferd, F. S., Cambon, C., Delache, A. & Bos, W. J. T. 2011 Quasi-static magnetohydrodynamic turbulence at high Reynolds number. J. Fluid Mech. 681, 434–461.CrossRefGoogle Scholar
13. Galletti, B. & Bottaro, A. 2004 Large-scale secondary structures in duct flow. J. Fluid Mech. 512, 85–94.CrossRefGoogle Scholar
14. Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.CrossRefGoogle Scholar
15. Hartmann, J. 1937 Hg-dynamics I: theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15 (6), 1–28.Google Scholar
16. Hartmann, J. & Lazarus, F. 1937 Hg-dynamics II: experimental investigations on the flow of mercury in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15 (7), 1–45.Google Scholar
17. Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
18. Jeong, J. & Hussein, F. 1995 On the identification of a vortex. J. Fluid Mech. 285 (1), 69–94.CrossRefGoogle Scholar
19. Johnston, J. P., Haleen, R. M. & Lezius, D. K. 1972 Effect of the spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56 (3), 533–557.CrossRefGoogle Scholar
20. Kassinos, C., Knaepen, B. & Wray, A. 2006 The structure of MHD turbulence subjected to mean shear and frame rotation. J. Turbul. 7 (1).CrossRefGoogle Scholar
21. Knaepen, B., Kassinos, S. & Carati, D. 2004 Magnetohydrodynamic turbulence at moderate magnetic Reynolds number. J. Fluid Mech. 513, 199–220.CrossRefGoogle Scholar
22. Kobayashi, H. 2006 Large eddy simulation of magnetohydrodynamic turbulent channel flows with local subgrid-scale model based on coherent structures. Phys. Fluids 18, 045107.CrossRefGoogle Scholar
23. Kobayashi, H. 2008 Large eddy simulation of magnetohydrodynamic turbulent duct flows. Phys. Fluids 20, 015102.CrossRefGoogle Scholar
24. Krasnov, D., Zikanov, O. & Boeck, T. 2011a Comparative study of finite difference approaches to simulation of magnetohydrodynamic turbulence at low magnetic Reynolds number. Comput. Fluids 50, 46–59.CrossRefGoogle Scholar
25. Krasnov, D., Zikanov, O., Rossi, M. & Boeck, T. 2010 Optimal linear growth in magnetohydrodynamic duct flow. J. Fluid Mech. 653, 273–299.CrossRefGoogle Scholar
26. Krasnov, D., Zikanov, O., Schumacher, J. & Boeck, T. 2008 Magnetohydrodynamic turbulence in a channel with spanwise magnetic field. Phys. Fluids 20 (9), 095105.CrossRefGoogle Scholar
27. Krasnov, D., Zikanov, O., Thess, A. & Boeck, T. 2011 b Direct numerical simulation of transition and turbulence in MHD duct flow. In The 8th PAMIR Conference on Fundamental and Applied MHD, pp. 157–161. Borgo.Google Scholar
28. Krasnov, D. S., Zienicke, E., Zikanov, O., Boeck, T. & Thess, A. 2004 Numerical study of instability and transition to turbulence in the Hartmann flow. J. Fluid Mech. 504, 183–211.CrossRefGoogle Scholar
29. Lee, D. & Choi, H. 2001 Magnetohydrodynamic turbulent flow in a channel at low magnetic Reynolds number. J. Fluid Mech. 429, 367–394.CrossRefGoogle Scholar
30. Moresco, P. & Alboussière, T. 2004 Experimental study of the instability of the Hartmann layer. J. Fluid Mech. 504, 167–181.CrossRefGoogle Scholar
31. Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143, 90–124.CrossRefGoogle Scholar
32. Müller, U. & Bühler, L. 2001 Magnetohydrodynamics in Channels and Containers. Springer.CrossRefGoogle Scholar
33. Murgatroyd, W. 1953 Experiments on magnetohydrodynamic channel flow. Phil. Mag. 44, 1348–1354.CrossRefGoogle Scholar
34. Ni, M.-J., Munipalli, R., Huang, P., Morley, N. B. & Abdou, M. A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part 1. On a rectangular collocated grid system. J. Comput. Phys. 227, 174–204.CrossRefGoogle Scholar
35. Potherat, A. 2007 Quasi-two-dimensional perturbations in duct flows under transverse magnetic field. Phys. Fluids 19, 074104.CrossRefGoogle Scholar
36. Potherat, A. & Schweitzer, J.-P. 2011 A shallow water model for magnetohydrodynamic flows with turbulent Hartmann layers. Phys. Fluids 23 (5), 055108.CrossRefGoogle Scholar
37. Potherat, A., Sommeria, J. & Moreau, R. 2000 An effective two-dimensional model for MHD flows with transverse magnetic field. J. Fluid Mech. 424, 75–100.CrossRefGoogle Scholar
38. Reed, C. B. & Lykoudis, P. S. 1978 The effect of a transverse magnetic field on shear turbulence. J. Fluid Mech. 89, 147–171.CrossRefGoogle Scholar
39. Sarris, I. E., Kassinos, S. C. & Carati, D. 2007 Large-eddy simulations of the turbulent Hartmann flow close to the transitional regime. Phys. Fluids 19 (8), 085109.CrossRefGoogle Scholar
40. Satake, S., Kunugi, T., Takase, K. & Ose, Y. 2006 Direct numerical simulation of turbulent channel flow under a uniform magnetic field for large-scale structures at high Reynolds number. Phys. Fluids 18 (12), 125106.CrossRefGoogle Scholar
41. Shatrov, V. & Gerbeth, G. 2010 Marginal turbulent magnetohydrodynamic flow in a square duct. Phys. Fluids 22, 084101.CrossRefGoogle Scholar
42. Sommeria, J. & Moreau, R. 1982 Why, how and when MHD-turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.CrossRefGoogle Scholar
43. Thess, A. & Zikanov, O. 2007 Transition from two-dimensional to three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 579, 383–412.CrossRefGoogle Scholar
44. Uhlmann, M., Pinelli, A., Kawahara, G. & Sekimoto, A. 2007 Marginally turbulent flow in a square duct. J. Fluid Mech. 588, 153–162.CrossRefGoogle Scholar
45. Vorobev, A., Zikanov, O., Davidson, P. A. & Knaepen, B. 2005 Anisotropy of magnetohydrodynamic turbulence at low magnetic Reynolds number. Phys. Fluids 17 (12), 125105.CrossRefGoogle Scholar
46. Zhao, Y. & Zikanov, O. 2012 Instabilities and turbulence in magnetohydrodynamic flow in a toroidal duct prior to transition in Hartmann layers. J. Fluid Mech. 692, 288–316.CrossRefGoogle Scholar
47. Zhao, Y., Zikanov, O. & Krasnov, D. 2011 Instability of magnetohydrodynamic flow in an annular channel at high Hartmann number. Phys. Fluids 23, 084103.CrossRefGoogle Scholar
48. Zikanov, O. & Thess, A. 1998 Direct numerical simulation of forced MHD turbulence at low magnetic Reynolds number. J. Fluid Mech. 358, 299–333.CrossRefGoogle Scholar