Article contents
Observations of hypervelocity boundary-layer instability
Published online by Cambridge University Press: 16 September 2015
Abstract
A novel optical method is used to measure the high-frequency (up to 3 MHz) density fluctuations that precede transition to turbulence within a laminar boundary layer in a hypervelocity flow. This optical method, focused laser differential interferometry, enables measurements of short-wavelength, high-frequency disturbances that are impossible with conventional instrumentation such as pressure transducers or hot wires. In this work, the T5 reflected-shock tunnel is used to generate flows in air, nitrogen and carbon dioxide with speeds between 3.5 and 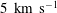 $5~\text{km}~\text{s}^{-1}$ (Mach numbers between 4 and 6) over a 5° half-angle cone at zero angle of attack. Simultaneous measurements are made at two locations approximately midway along a generator of the 1-m-long cone. With increasing Reynolds number (unit values were between 2 and
$5~\text{km}~\text{s}^{-1}$ (Mach numbers between 4 and 6) over a 5° half-angle cone at zero angle of attack. Simultaneous measurements are made at two locations approximately midway along a generator of the 1-m-long cone. With increasing Reynolds number (unit values were between 2 and 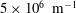 $5\times 10^{6}~\text{m}^{-1}$), density fluctuations are observed to grow in amplitude and transition from a single narrow band of frequencies consistent with the Mack or second mode of boundary-layer instability to bursts of large-amplitude and spectrally broad disturbances that appear to be precursors of turbulent spots. Disturbances that are sufficiently small in initial amplitude have a wavepacket-like signature and are observed to grow in amplitude between the upstream and downstream measurement locations. A cross-correlation analysis indicates propagation of wavepackets at speeds close to the edge velocity. The free stream flow created by the shock tunnel and the resulting boundary layer on the cone are computed, accounting for chemical and vibrational non-equilibrium processes. Using this base flow, local linear and parabolized stability (PSE) analyses are carried out and compared with the experimental results. Reasonable agreement is found between measured and predicted most unstable frequencies, with the greatest differences being approximately 15 %. The scaling of the observed frequency with the inverse of boundary-layer thickness and directly with the flow velocity are consistent with the characteristics of Mack’s second mode, as well as results of previous researchers on hypersonic boundary layers.
$5\times 10^{6}~\text{m}^{-1}$), density fluctuations are observed to grow in amplitude and transition from a single narrow band of frequencies consistent with the Mack or second mode of boundary-layer instability to bursts of large-amplitude and spectrally broad disturbances that appear to be precursors of turbulent spots. Disturbances that are sufficiently small in initial amplitude have a wavepacket-like signature and are observed to grow in amplitude between the upstream and downstream measurement locations. A cross-correlation analysis indicates propagation of wavepackets at speeds close to the edge velocity. The free stream flow created by the shock tunnel and the resulting boundary layer on the cone are computed, accounting for chemical and vibrational non-equilibrium processes. Using this base flow, local linear and parabolized stability (PSE) analyses are carried out and compared with the experimental results. Reasonable agreement is found between measured and predicted most unstable frequencies, with the greatest differences being approximately 15 %. The scaling of the observed frequency with the inverse of boundary-layer thickness and directly with the flow velocity are consistent with the characteristics of Mack’s second mode, as well as results of previous researchers on hypersonic boundary layers.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 108
- Cited by


